用Burg法估计AR模型的参数原理详解及matlab实现
用Burg法估计AR模型的参数。
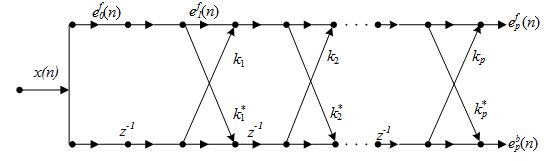
借助如图所示的格型预测误差滤波器,伯格法通过求出前向预测误差和后向预测误差的平均功率来选取最佳的反射系数k,使误差的平均功率取得最小值,进而通过反馈求出模型系数和噪声方差,该算法可直接通过分析观测数据得到需要的模型参数,而不用取求解计算量较大自相关函数,
burg法的实现原理
其实AR模型用来估计功率谱是很好用的,比传统的Welch算法好很多,矩形性很好,用来估计信号的矩形等效带宽效果很好
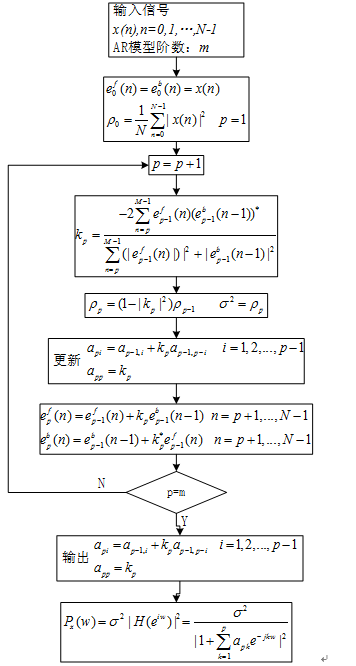
用Burg法估计AR模型的参数的流程图
matlab代码为:CSDN中没有matlab专属的,为了好看就这样贴代码了,哼~~~~~~~~~~~~~
function [psdviaBurg, f, p] = Burg(x, Fs, varargin)
%MYBURG 根据burg算法实现的AR模型功率谱计算
% psdviaBurg 根据burg算法求出的功率谱值
% f 频率轴参数
% p 模型阶次
% x 输出信号
% Fs 采样率
% varargin 若为数值型,则为AR模型阶次
% 若为字符串,则为定阶准则,AR模型阶次由程序确定
%
% 解析输入参数内容
if strcmp(class(varargin{1}), 'double')
p = varargin{1};
elseif ischar(varargin{1})
criterion = varargin{1};
else
error('参数2必须为数值型或者字符串');
end
x = x(:);
N = length(x);
% 模型参数求解
if exist('p', 'var') % p变量是否存在,存在则不需要定阶,直接使用p阶
[a, E] = computeARpara(x, p);
else % p不存在,需要定阶,定阶准则即criterion
p = ceil(N/3); % 阶次一般不超过信号长度的1/3
% 计算1到p阶的误差
[a, E] = computeARpara(x, p);
% 根据误差求解目标函数最小值
kc = 1:p + 1;
switch criterion
case 'FPE'
goalF = E.*(N + (kc + 1))./(N - (kc + 1));
case 'AIC'
goalF = N.*log(E) + 2.*kc;
end
[minF, p] = min(goalF); % p就是目标函数最小的位置,也即定阶准则给出的阶次
% 使用p阶重新求解AR模型参数
[a, E] = computeARpara(x, p);
end
[h, f] = freqz(1, a, 20e5, Fs);
psdviaBurg = E(end)*abs(h).^2./Fs;
psdviaBurg=psdviaBurg/abs(max(psdviaBurg));
psdviaBurg=(10*log10(abs(psdviaBurg)));还缺个函数,就是根据给定的数据来计算AR模型的参数和误差,并最小化误差,这个包含了AR模型的核心的算法
function [a, E] = computeARpara(x, p)
% 根据信号序列x和阶次p计算AR模型参数和误差
N = length(x);
% 初始值
ef = x; % 前向预测误差
eb = x; % 后向预测误差
a = 1; % 初始模型参数
E = x'*x/N; % 初始误差
k = zeros(1, p); % 为反射系数预分配空间,提高循环速度
E = [E k]; % 为误差预分配空间,提高速度
for m = 1:p
% 根据burg算法步骤,首先计算m阶的反射系数
efm = ef(2:end); % 前一阶次的前向预测误差
ebm = eb(1:end - 1); % 前一阶次的后向预测误差
num = -2.*ebm'*efm; % 反射系数的分子项
den = efm'*efm + ebm'*ebm; % 反射系数的分母项
k(m) = num./den; % 当前阶次的反射系数
% 更新前后向预测误差
ef = efm + k(m)*ebm;
eb = ebm + conj(k(m))*efm;
% 更新模型系数a
a = [a; 0] + k(m)*[0; conj(flipud(a))];
% 当前阶次的误差功率
E(m + 1) = (1 - conj(k(m))*k(m))*E(m);
end