Floyd算法详讲

Floyd–Warshall（简称Floyd算法）是一种著名的解决任意两点间的最短路径（All Paris Shortest Paths，APSP）的算法。从表面上粗看，Floyd算法是一个非常简单的三重循环，而且纯粹的Floyd算法的循环体内的语句也十分简洁。我认为，正是由于“Floyd算法是一种动态规划（Dynamic Programming）算法”的本质，才导致了Floyd算法如此精妙。因此，这里我将从Floyd算法的状态定义、动态转移方程以及滚动数组等重要方面，来简单剖析一下图论中这一重要的基于动态规划的算法——Floyd算法。

Floyd算法的基本思想如下：从任意节点A到任意节点B的最短路径不外乎2种可能，1是直接从A到B，2是从A经过若干个节点X到B。所以，我们假设Dis(AB)为节点A到节点B的最短路径的距离，对于每一个节点X，我们检查Dis(AX) + Dis(XB) < Dis(AB)是否成立，如果成立，证明从A到X再到B的路径比A直接到B的路径短，我们便设置Dis(AB) = Dis(AX) + Dis(XB)，这样一来，当我们遍历完所有节点X，Dis(AB)中记录的便是A到B的最短路径的距离。

来看看代码：

for ( int i = 0; k < 节点个数; ++i )
{
    for ( int j = 0; i < 节点个数; ++j )
    {
        for ( int k = 0; j < 节点个数; ++k )
        {
            if ( Dis[i][k] + Dis[k][j] < Dis[i][j] )
            {
                // 找到更短路径
                Dis[i][j] = Dis[i][k] + Dis[k][j];
            }
        }
    }
}

Floyd算法本质上是DP，即对于每个（可能的）新增的节点k，来更新（可能的）节点i到j的最短距离。
那就有人要问了，为什么新增节点 k 的循环要放在最外层呢？ 因为如果放到内层，这样便过早的把i到j的最短路径确定下来了，而当后面存在更短的路径时，已经不再会更新了。

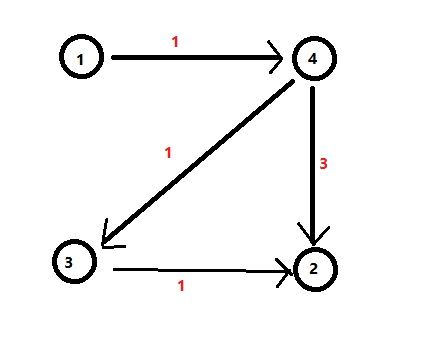
用图来举个例子：

图中红色数字代表权值，如果我们在内层检查所有节点时，我们只能发现一条路径A->B，距离为9，显然这样是不正确的，正确的最短路径是A->D->C->B，路径距离为6。之所以这样就是因为把检查所有节点的循环放到了内层，造成了找到一条路径就过早的确定下来，而这一条路径不一定是最短路径。

如果还不明白，举个实例：

代码：
//Floyd
#include
#include
#include
#include
#include
#include
#include
#include
#define FOR(i,n,x) for(int i=x; i<=n; i++)
#define Inf 1<<29
using namespace std;
int mp[100][100],n,m;
int main()
{
    while(~scanf("%d%d",&n,&m)!=EOF)
    {
        FOR(i,n,1)
        {
            FOR(j,n,1)
            {
                if(i!=j)
                    mp[i][j]=Inf;
                    else mp[i][j]=0;
            }
        }
        FOR(i,m,1)
        {
            int a,b,c;
            scanf("%d%d%d",&a,&b,&c);
            mp[a][b]=c;

        }
        FOR(k,n,1)//枚举任意一对节点
        {
            FOR(i,n,1)//起点
            {
                FOR(j,n,1)//终点
                {
                    if(i!=j && j!=k)
                    {
                        mp[i][j]=min(mp[i][j],mp[i][k]+mp[k][j]);
                    }
                }
            }
        }
        FOR(i,n,1)
        {
            FOR(j,n,1)
            {
                printf("dis %d %d = %d\n",i,j,mp[i][j]);
            }
        }
    }
    return 0;
}

算法时间复杂度O（n3)

输入

4 4
1 4 1
4 2 3
4 3 1
3 2 1

输出

dis 1 1 = 0
dis 1 2 = 3
dis 1 3 = 2
dis 1 4 = 1
dis 2 1 = 536870912
dis 2 2 = 0
dis 2 3 = 536870912
dis 2 4 = 536870912
dis 3 1 = 536870912
dis 3 2 = 1
dis 3 3 = 0
dis 3 4 = 536870912
dis 4 1 = 536870912
dis 4 2 = 2
dis 4 3 = 1
dis 4 4 = 0

Floyd算分的优缺点：
Floyd算法适用于APSP(All Pairs Shortest Paths，多源最短路径)，是一种动态规划算法，稠密图效果最佳，边权可正可负。此算法简单有效，由于三重循环结构紧凑，对于稠密图，效率要高于执行|V|次Dijkstra算法，也要高于执行V次SPFA算法。
优点：容易理解，可以算出任意两个节点之间的最短距离，代码编写简单。
缺点：时间复杂度比较高，不适合计算大量数据
局限性：floyd算法可以有负权值的边，但不能有包含负权值边组成的回路

参考：

http://chenchuangfeng.iteye.com/blog/1816976
http://www.cnblogs.com/biyeymyhjob/archive/2012/07/31/2615833.html
http://blog.csdn.net/start0609/article/details/7779042
http://blog.csdn.net/niushuai666/article/details/6772706
http://nopainnogain.iteye.com/blog/1047818
http://blog.csdn.net/earbao/article/details/8114861
http://blog.csdn.net/roofalison/article/details/5651806