字符串的编辑距离(LeetCode: 72. Edit Distance)-动态规划-Python
问题描述:
给定两个字符串A和B,要用最少的操作将字符串A转换成字符串B。其中字符串操作包括:
(1)删除一个字符(Insert a character)
(2)插入一个字符(Delete a character)
(3)修改一个字符(Replace a character)
将字符串A转换成B串所用的最少字符操作数称为字符串A到 B的编辑距离,又称为Levenshtein距离,是在1965年,俄罗斯数学家Vladimir Levenshtein提出的。
问题分析:动态规划思想
(1)、dp[i][j]表示将字符串 A[0: i-1] 转变为 B[0: j-1] 的最小步骤数。
(2)、边界情况:
当 i = 0 , 即 A 串为空时,那么转变为 B 串就是不断添加字符,dp[0][j] = j。
当 j = 0,即 B 串为空时,那么转变为 B 串就是不断删除字符,dp[i][0] = i。
(3)、对应三种字符操作方式:
插入操作:dp[i][j - 1] + 1 相当于为 B 串的最后插入了 A 串的最后一个字符;
删除操作:dp[i - 1][j] + 1 相当于将 B 串的最后字符删除 ;
替换操作:dp[i - 1][j - 1] +(A[i - 1] != B[j - 1])相当于通过将 B 串的最后一个字符替换为 A 串的最后一个字符。
(4)所以dp方程式为:
1<=i<=len(A), 1<=j<=len(B)
dp[i][j] = dp[i-1][j-1], A[i-1] == B[j-1]
dp[i][j] = min(dp[i-1][j-1]+1, dp[i][j-1]+1, dp[i-1][j]+1), A[i-1] != B[j-1]
Python实现(时间复杂度:O(mn),空间复杂度:O(mn)):
class Solution:
def minDistance(self, word1, word2):
"""
:type word1: str
:type word2: str
:rtype: int
"""
m, n = len(word1), len(word2)
if m == 0:return n
if n == 0:return m
dp = [[0]*(n+1) for _ in range(m+1)] # 初始化dp和边界
for i in range(1, m+1): dp[i][0] = i
for j in range(1, n+1): dp[0][j] = j
for i in range(1, m+1): # 计算dp
for j in range(1, n+1):
if word1[i - 1] == word2[j - 1]:
dp[i][j] = dp[i - 1][j - 1]
else:
dp[i][j] = min(dp[i - 1][j - 1] + 1, dp[i][j - 1] + 1, dp[i - 1][j] + 1)
return dp[m][n]
if __name__ == '__main__':
solu = Solution()
word1, word2 = 'horse', 'ros'
print(solu.minDistance(word1, word2))优化dp空间:
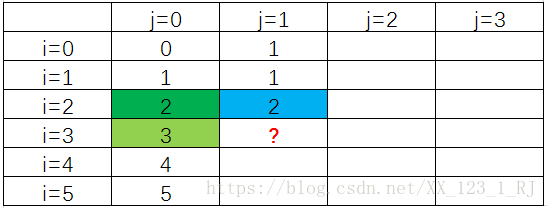
很多两维的dp空间是可以压缩成一维的,用一个例子说明,word1, word2 = 'horse', 'ros',所以得到的dp空间为:
现在要求i=3,j=1的值?必须知道这个方格的左边、左上角、上边,三个方格的值,那么思路来了,我们一列一列的计算,用一个cur[i]数据保存当前列数值,且,再开辟两个变量,pre、temp,用来保存当前方格的左上角、和左边方格的值,cur[i]每更新一次对应的pre、temp也向下滑动一次,就这样只保留一列的信息,依次向右计算直至结束。所以现在可以把空间复杂度降到O(m) 或者O(n),时间复杂度不变。
Python优化实现(时间复杂度:O(mn),空间复杂度:O(m) or O(n)):
# @Time :2018/6/18
# @Author :LiuYinxing
class Solution:
def minDistance(self, word1, word2):
m, n = len(word1), len(word2)
if m == 0: return n
if n == 0: return m
cur = [0] * (m + 1) # 初始化cur和边界
for i in range(1, m+1): cur[i] = i
for j in range(1, n+1): # 计算cur
pre, cur[0] = cur[0], j # 初始化当前列的第一个值
for i in range(1, m+1):
temp = cur[i] # 取出当前方格的左边的值
if word1[i - 1] == word2[j - 1]:
cur[i] = pre
else:
cur[i] = min(pre + 1, cur[i] + 1, cur[i - 1] + 1)
pre = temp
return cur[m]
if __name__ == '__main__':
solu = Solution()
word1, word2 = 'horse', 'ros'
print(solu.minDistance(word1, word2))