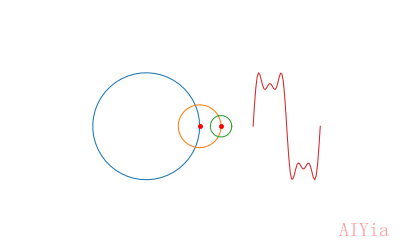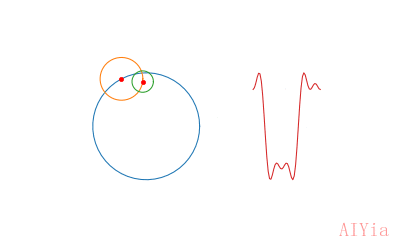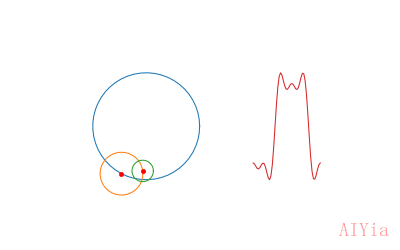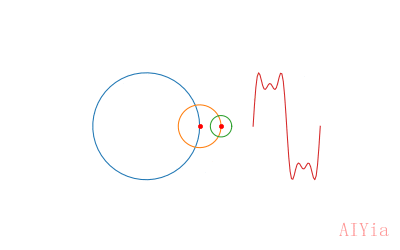
用python动态生成波形曲线

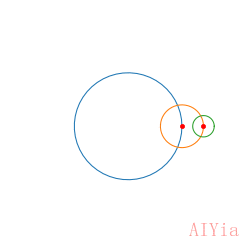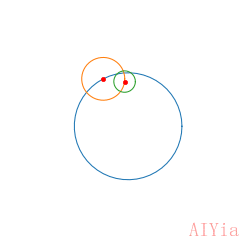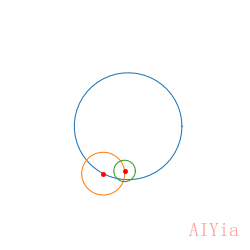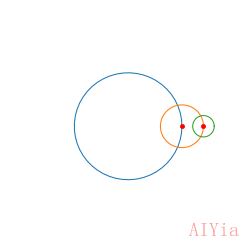
  效果是这个样子的：

用到的模块:
* matplotlib.pyplot
* matplotlib.animation.FuncAnimation
* numpy
三个圆的半径分别为：5， 2， 1。
三个点旋转的角频率分别为：1， 3， 5。

生成固定的圆——基础圆

xdata = np.linspace(0, 2 * np.pi, 50)
fig, ax = plt.subplots(1, 1, figsize=(8, 5))
b_cir = ax.plot(5 * np.cos(xdata), 5 * np.sin(xdata))

# 配置下画布
ax.spines['bottom'].set_visible(False)    # 清除下脊
ax.spines['top'].set_visible(False)       # 清除上脊
ax.spines['left'].set_visible(False)      # 清除左脊
ax.spines['right'].set_visible(False)     # 清除右脊
# 取消刻度和数字标签
ax.tick_params(bottom='off', left='off', labelbottom='off', labelleft='off')

生成第1个移动点

  根据圆上点的坐标公式，更新点的位置：
x = r * cos(w * t) + a
y = r * sin(w * t) + b

def update(frame):
    movX1 = 5 * np.cos(frame * 1)
    movY1 = 5 * np.sin(frame * 1)
    movp1.set_data(movX1, movY1)    # 更新移动点数据
    return movp1,     # 还是得有','
ani = FuncAnimation(fig, update, frames=xdata, blit=True)

生成第1个移动圆

  根据坐标系中任意位置上圆的公式，计算移动的圆。

c_sub1, = ax.plot([], [], animated=True)
# 修改 update 函数生成在基础圆上移动的圆
def update(frame):
    # 计算移动点
    # 计算移动圆
    c_sub1X = 2 * np.cos(xdata) + movX1
    c_sub1Y = 2 * np.sin(xdata) + movY1
    # 更新移动点数据
    c_sub1.set_data(c_sub1X, c_sub1Y)
    return movp1, c_sub1,

生成第2个移动点和移动圆

   生成的方式和前面的类似

movp2, = ax.plot([], [], 'ro', animated=True)
c_sub2, = ax.plot([], [], animated=True)
def update(frame):
# 计算第1个移动点和圆
# 计算第2个移动点和圆
movX2 = movX1 + 2 * np.cos(frame * 3)
movY2 = movY1 + 2 * np.sin(frame * 3)
c_sub2X = 1 * np.cos(xdata) + movX2
c_sub2Y = 1 * np.sin(xdata) + movY2

# 更新第1个移动点和圆
# 更新第2个移动点和圆
movp2.set_data(movX2, movY2)
c_sub2.set_data(c_sub2X, c_sub2Y)
return movp1, c_sub1, movp2, c_sub2,

生成波形曲线

  生成的波形曲线，其实就是3个圆生成的正弦曲线的叠加值:
sineTotal = sine1 + sine2 + sine3

sine, = ax.plot(xdata + 10, np.zeros(50))
def update(frame):
# 计算第1个移动点和圆
# 计算第2个移动点和圆
# 计算波形曲线的 y 值
s = 5 * np.sin((xdata+frame) * 1) + \
    2 * np.sin((xdata+frame) * 3) + \
    1 * np.sin((xdata+frame) * 5)

# 更新第1个移动点和圆
# 更新第2个移动点和圆
# 更新波形曲线
sine.set_ydata(s)
return movp1, c_sub1, movp2, c_sub2, sine,

加条直线指示下

  直线就是，第3个移动圆上的移动点与波形末端的连线。

movp3, = ax.plot([], [], 'ro', animated=True)  # 添加第3个圆上的移动点
ln, = ax.plot([], [], animated=True)
def update(frame):
# 计算第1个移动点和圆
# 计算第2个移动点和圆
# 计算波形曲线的 y 值
# 计算第3个移动点
movX3 = movX2 + 1 * np.cos(frame * 5)
movY3 = movY2 + 1 * np.sin(frame * 5)

# 更新第1个移动点和圆
# 更新第2个移动点和圆
# 更新波形曲线
ln.set_data([movX3, 10 + 2 * np.pi], [movY3, movY3])
return movp1, c_sub1, movp2, c_sub2, sine, movp3, ln

保存 gif 动图

ani.save("multiSin.gif", writer='imagemagick', fps=200, dpi=50)

  这里用到“imagemagick”来进行动图的保存。但在使用前需要配置些内容：
1. 安装 imagemagick，下载地址是：http://www.imagemagick.org/script/download.php；
2. 修改matplotlibrc文件进行配置，可通过下面语句查看文件存放路径：

import matplotlib
matplotlib.matplotlib_fname()

  在文件末尾取消“animation.convert_path”的注释；
3. 修改__init__.py文件，打开文件后查找rcParams()，在下一行添加：

rcParams['animation.convert_path'] = '[imagemagick的安装路径]\\ImageMagick-7.0.8-Q16\\magick.exe'

  在以前的imagemagick版本，有个文件是convert.exe，新版本这个文件取消了，功能整合到“magick.exe”中了。

修改完成后就可以使用上面的语句生成gif动图了。