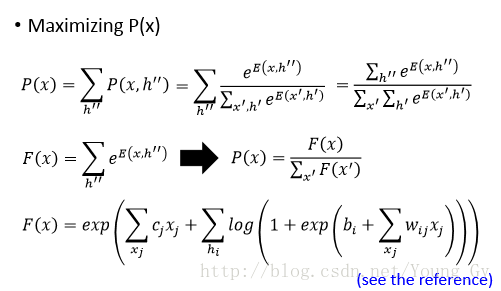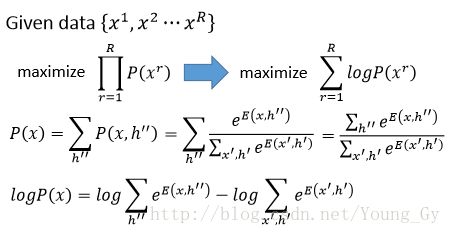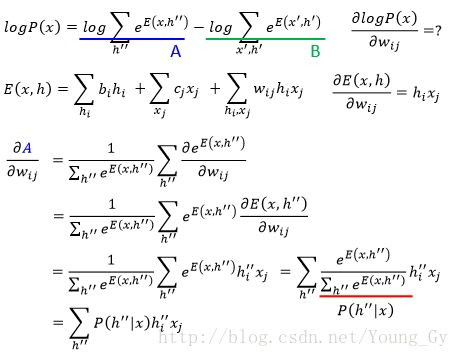无监督学习之RBM和AutoEncoder
- 几种学习方式
- 半监督学习
- Transfer Learning
- Self-talk Learning
- RBM
- RBM的类别
- Boltzmann Machine
- Restricted Boltzmann Machine
- Evaluation
- Inference
- Training
- 网络结构
- 训练过程
- 概率分布计算与Gibbs Sampling
- 对比散度Contrastive Divergence
- 泛化
- 实例
- AutoEncoder
- 特点
- 实例
有标签的数据固然好,可是一方面打标签的代价太高,另一方面大部分数据是无标签的。这样就涉及到无监督、半监督、Self-taught学习的问题。本文将介绍两种适用于无标签数据的学习方法,可以找到数据中的隐含模式,包括RBM和AutoEncoder。
几种学习方式
以识别猫狗图像为例,区分以下几种学习方式。
- 监督学习:有标签的猫狗数据。
- 无监督学习:无标签的猫狗数据。
- 半监督学习:部分有标签的猫狗数据。
- Transfer Learning:有标签的猫狗数据、有标签的大象老虎的数据。
- Self-taught Learning:有标签的猫狗数据、无标签的大象老虎美女的数据。
半监督学习
有时候,考虑无标签的数据分布,我们可能可以把分类器做得更好。
首先,可以先用有标签的数据训练得到分类器 C0 ,然后用 C0 去预测无标签的数据并打上标签。最后使用全部的数据训练得到分类器 C1 。
Transfer Learning
Transfer Learning,本质上是希望通过与目标对象不那么相关的数据(例如利用大象老虎的图片去分类猫狗的图片)发现潜在的共性特征,利用潜在的共性特征去分类识别。
在图像识别中,经常使用Transfer Learning的方法。其思路是:先利用CNN训练一大堆数据,CNN的隐含层相当于特征提取层。用于新的数据时,保持原来的网络结构的前面部分不变,相当于构建了隐含特征,通过调整后面部分的网络参数实现对新数据的识别。
在日常生活中,也有Transfer Learning的例子。有本叫《爆漫王》的漫画,讲的是一位少年努力成为漫画家的故事。其实漫画家和研究生蛮像的,责编-导师、画分镜-跑实验、投稿jump-投稿期刊。不过,人家的漫画家比咱研究生努力多了,生病住院的时候还在画分镜,研究生很少有住院拿键盘code的吧。
Self-talk Learning
Self-talk Learning与Transfer Learning很像,都有除了猫狗以外的大象老虎的数据。不同之处是:Transfer Learning的大象老虎数据是有标签的,Self-talk Learning的大象老虎数据是无标签的。
Self-talk Learning的例子如下:
- 识别数字0-9,有a-z的无标签的字符数据
- 新闻文本分类,有网络上爬的各种文本
- 汉语识别,有网络上英语、西班牙语的语料数据
乍看之下,Self-talk Learning很难,从不相关的无标签数据中可以获得什么呢?仔细思考下,以图像为例,像素空间的向量分布是很稀疏的,实际空间的维度并不需要这么高。不论是0-9还是a-z都是由不同的笔触组成的,如果可以通过无监督的a-z学习到笔触的表现形式,那么对于0-9的数据,先转化成笔触再进行识别便有可能取得较高的识别精度。
RBM
RBM的类别
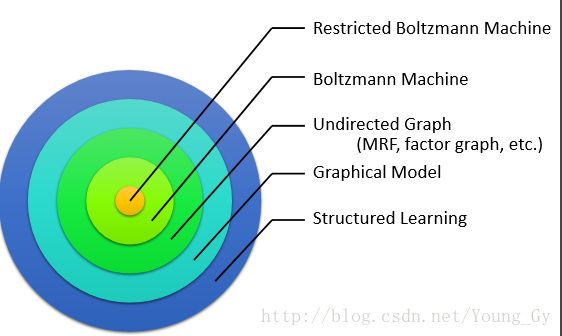
RBM属于图模型的一种,具体来说,有:
Boltzmann Machine
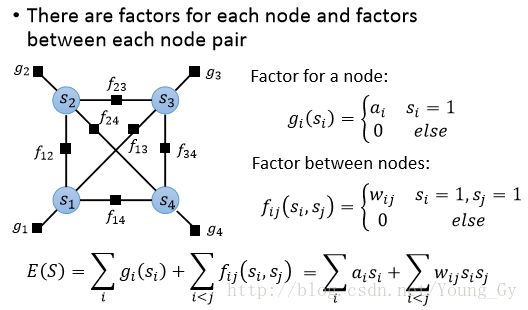
Boltzmann Machine,评判了一组集合可能情况的分数,设集合 S={s1,...sK} , si∈{0,1} ,定义评估函数如下:
将评估函数转化成概率的话,公式如下:
从图模型的角度理解,Boltzmann Machine相当于factor graph。对于每个节点 si ,以及每个节点对 (si,sj) ,都有一个factor与之对应。
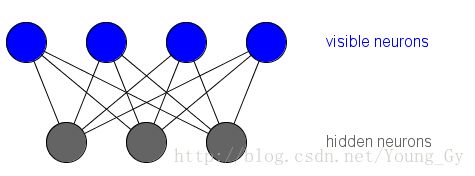
Restricted Boltzmann Machine
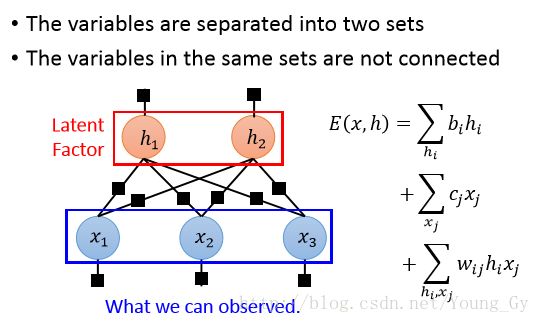
受限玻尔兹曼机,在原玻尔兹曼机的集合 S={s1,...sK} 基础上,增加了新的隐含集合 H={h1,...hK} 。其本质也是factor graph,factor存在于所有的node上,同时原来玻尔兹曼机中两两相连的node对 {si,sj} 取消了,换成了node对 {si,hj} 。其图模型的具体表示为:
RBM或者Restricted RBM主要由三部分组成:
- Evaluation:如何评估当前的状态好坏,对应 E(x,h) 或 P(x,h)
- Inference:给定 x ,计算 P(hj=1|x)
- Training:如何训练得到模型的参数 w,b,c
Evaluation
对于RBM:
对于Restricted RBM:
Inference
Restricted RBM本质是无向图,根据图论有:
- 给定x,所有的h独立
- 给定h,所有的x独立
那么, P(hi=1|x) 的计算公式为:
这个公式中,相当于x是输入层,h是隐含层,输入层与隐含层之间全连接。激活函数是sigmoid函数。需要注意的是,Restricted RBM本质是无向图,而不是神经网络那样的有向图,只不过做inference的时候计算方法与神经网络的forward部分相近。
同样的,也可以类比计算 P(x|h) (这个在训练过程中的gibbs采样中会用到)。
Training
前面叙述了Restricted RBM的Evaluation和Inference,下面就剩下如何去Training了。Restricted RBM的训练采用了最大似然法,最大似然已知数据出现的概率。已知数据的概率 P(x) 通过 P(x,h) 做margin得到。有了最大似然的目标函数,然后采用梯度上升法求解即可。
目标为:
网络结构
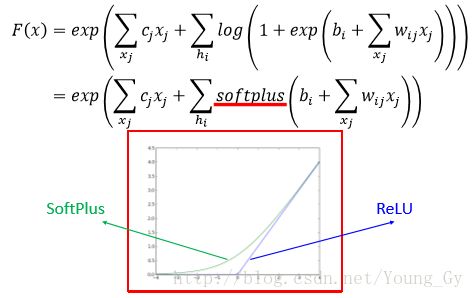
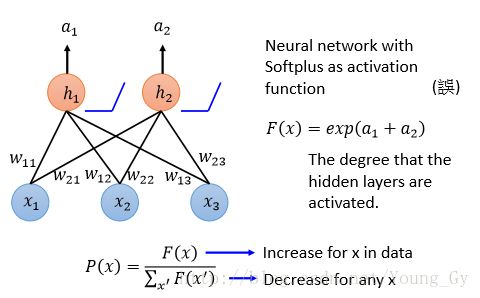
训练的优化目标是最大 P(x) ,通过转化等效对于带有softplus激活函数的网络,增加已知数据的激活度 F(x) ,减少任意数据的激活度 F(x) 。
训练过程
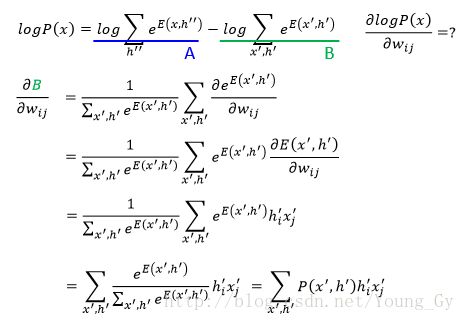
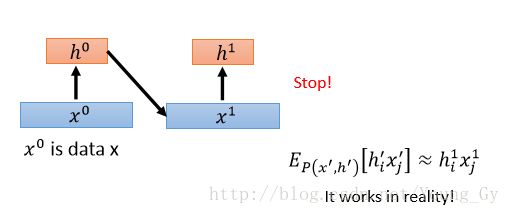
目标函数是最大似然函数 max∏Rr=1P(xr) ,训练的时候求目标函数对参数的梯度即可,相关数学公式如下:
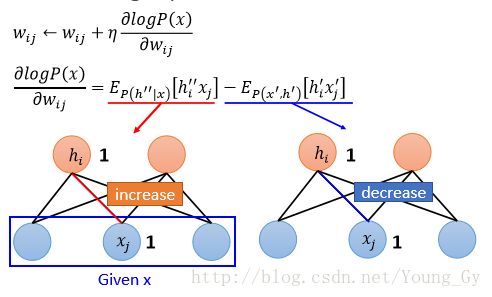
最后通过训练,得到的概率公式如下,其物理含义是增加看到数据的激活强度,减少未看到数据的激活强度。
概率分布计算与Gibbs Sampling
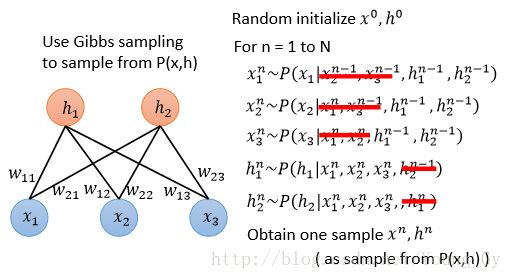
在训练的梯度更新式中,需要计算 P(h|x) 与 P(h,x) ,这两个概率分布可以通过Gibbs Sampling得到。
Gibbs Sampling中,外循环遍历样本数,内循环遍历特征数,对于每个特征,根据该特征的条件概率分布进行采样。
因为受限玻尔兹曼机 x 和 h 的条件独立性,可以在采样的时候做适当简化,最后等效于类似神经网络计算的采样。
对比散度Contrastive Divergence
gibbs采样的目的是获得概率分布,进而获得梯度上升中的更新梯度。那么,在做梯度上升的过程中,每次更新梯度都得计算概率分布也都得进行gibbs采样,这样会导致计算量非常大。
通常情况下,计算一次吉布斯采样即可,并用第一次采样的概率分布当做之后的概率分布。
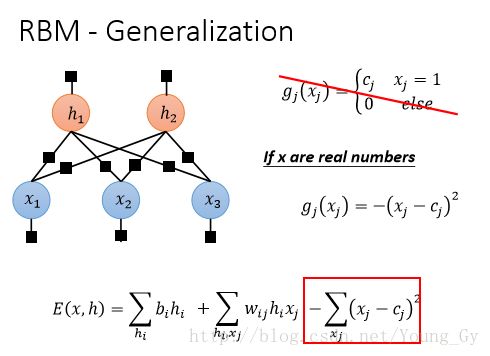
泛化
上文讲的RBM是针对 x,h 都是01值的,如果x不是01值,只需要改相应factor的计算公式即可。
实例
- 针对手写字体识别,可以做RBM的无监督学习,最后将每个隐含层对应的权重转化成图片,可以发现,每个隐含层相当于识别特定的笔触模式,可以视为特征提取器。
- RBM的隐含层不一定得一层,可以做多层的RBM得到更为抽象的特征。
- RBM可以用来预训练神经网络,训练的时候除了输出层与前一个隐含层不做RBM其他都做RBM。这个在10年之前用的比较多,10年之后大家用relu之后便不用RBM了。
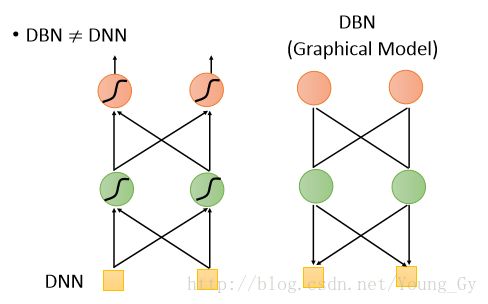
- DBN和DNN是不一样的。
AutoEncoder
特点
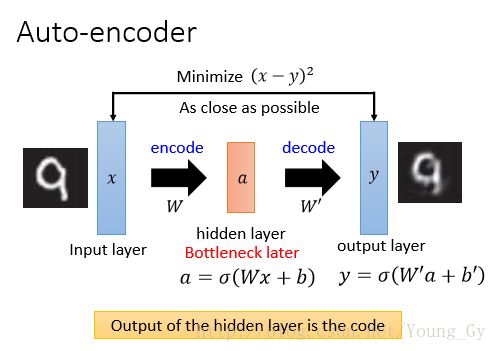
- 自编码器相当于通过网络重构数据。
- 自编码器如果隐含层是1层,激活函数是线性,输入数据做了均值化,那么等效于PCA。
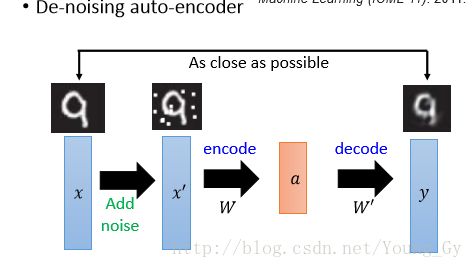
- 自编码器为了增加泛化能力,一般会增加噪声构成de-noising自编码器。同时也可以增加一些正则项提高泛化能力。
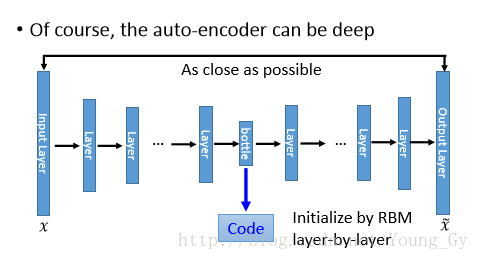
- 自编码器可以提高网络层数获得更深更抽象的表征能力。
实例
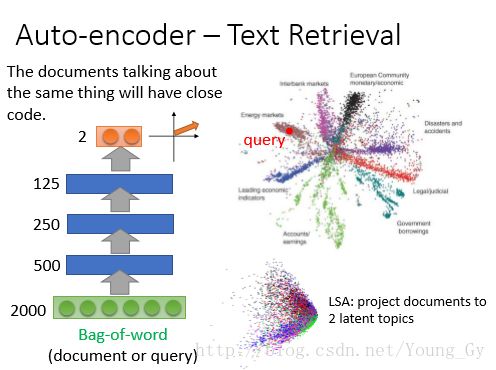
- 通过自编码器做text retrival(bag of wards会遇到同义词认为不一样的问题)。
- 通过自编码器做picture retrival。
- 通自编码器预训练神经网络。