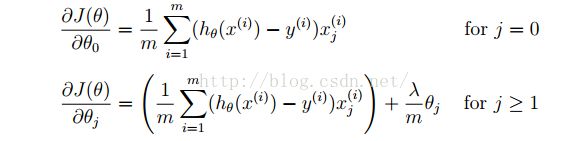Regularized logistic regression
声明：本博客内容参考了网上的代码，若有处理的不当的地方请指正！
Problem:
In this part of the exercise, you will implement regularized logistic regression to predict whether microchips from a fabrication plant passes quality assurance (QA). During QA, each microchip goes through various tests to ensure it is functioning correctly.
Suppose you are the product manager of the factory and you have the test results for some microchips on two different tests. From these two tests,you would like to determine whether the microchips should be accepted or rejected. To help you make the decision, you have a dataset of test results on past microchips, from which you can build a logistic regression model.
1.Feature mapping
One way to fit the data better is to create more features from each data point. In the provided function mapFeature.m, we will map the features into all polynomial terms of x1 and x2 up to the sixth power.
As a result of this mapping, our vector of two features (the scores on two QA tests) has been transformed into a 28-dimensional vector. A logistic regression classifier trained on this higher-dimension feature vector will have a more complex decision boundary and will appear nonlinear when drawn in our 2-dimensional plot.
While the feature mapping allows us to build a more expressive classifier,it also more susceptible to overfitting. In the next parts of the exercise, you will implement regularized logistic regression to fit the data and also see for yourself how regularization can help combat the overfitting problem.
mapFeature.m代码如下：
function out = mapFeature(X1, X2)
% MAPFEATURE Feature mapping function to polynomial features
%
% MAPFEATURE(X1, X2) maps the two input features
% to quadratic features used in the regularization exercise.
%
% Returns a new feature array with more features, comprising of
% X1, X2, X1.^2, X2.^2, X1*X2, X1*X2.^2, etc..
%
% Inputs X1, X2 must be the same size
%
degree = 6;
out = ones(size(X1(:,1)));
for i = 1:degree
for j = 0:i
out(:, end+1) = (X1.^(i-j)).*(X2.^j);
end
end
end2.Cost function and gradient
Recall that the regularized cost function in logistic regression is:
Note that you should not regularize the parameterθ0. In Matlab, recall that indexing starts from 1, hence, you should not be regularizing the theta(1) parameter (which corresponds toθ0) in the code. The gradient of the cost function is a vector where the jth element is defined as follows:
MATLAB代码如下：
function [J, grad] = costFunctionReg(theta, X, y, lambda)
%COSTFUNCTIONREG Compute cost and gradient for logistic regression with regularization
% J = COSTFUNCTIONREG(theta, X, y, lambda) computes the cost of using
% theta as the parameter for regularized logistic regression and the
% gradient of the cost w.r.t. to the parameters.
% Initialize some useful values
m = length(y); % number of training examples
% You need to return the following variables correctly
J = 0;
grad = zeros(size(theta));
% ====================== YOUR CODE HERE ======================
% Instructions: Compute the cost of a particular choice of theta.
% You should set J to the cost.
% Compute the partial derivatives and set grad to the partial
% derivatives of the cost w.r.t. each parameter in theta
theta_1=theta(2:end);
J= -1 * sum( y .* log( sigmoid(X*theta) ) + (1 - y ) .* log( (1 - sigmoid(X*theta)) ) ) / m + lambda/(2*m) * theta_1' * theta_1 ;%theta(1)拿掉，不参与正则化
grad = ( X' * (sigmoid(X*theta) - y ) )/ m + lambda/m * [0;theta_1] ;%theta_1的第一个为0
% =============================================================
end
后面的均与logistic regression一样的
完整代码参见：http://download.csdn.net/detail/zhe123zhe123zhe123/9543042