2019.08.22 日常总结

洛谷：

题意：

我国的离婚率连续7年上升，今年的头两季，平均每天有近5000对夫妇离婚，大城市的离婚率上升最快，有研究婚姻问题的专家认为，是与简化离婚手续有关。

25岁的姗姗和男友谈恋爱半年就结婚，结婚不到两个月就离婚，是典型的“闪婚闪离”例子，而离婚的导火线是两个人争玩电脑游戏，丈夫一气之下，把电脑炸烂。

有社会工作者就表示，80后求助个案越来越多，有些是与父母过多干预有关。而根据民政部的统计，中国离婚五大城市首位是北京，其次是上海、深圳，广州和厦门，那么到底是什么原因导致我国成为离婚大国呢?有专家分析说，中国经济急速发展，加上女性越来越来越独立，另外，近年来简化离婚手续是其中一大原因。

——以上内容摘自第一视频门户

现代生活给人们施加的压力越来越大，离婚率的不断升高已成为现代社会的一大问题。而其中有许许多多的个案是由婚姻中的“不安定因素”引起的。妻子与丈夫吵架后，心如绞痛，于是寻求前男友的安慰，进而夫妻矛盾激化，最终以离婚收场，类似上述的案例数不胜数。

我们已知n对夫妻的婚姻状况，称第i对夫妻的男方为Bi，女方为Gi。若某男Bi与某女Gj曾经交往过（无论是大学，高中，亦或是幼儿园阶段，i≠j），则当某方与其配偶（即Bi与Gi或Bj与Gj）感情出现问题时，他们有私奔的可能性。不妨设Bi和其配偶Gi感情不和，于是Bi和Gj旧情复燃，进而Bj因被戴绿帽而感到不爽，联系上了他的初恋情人Gk……一串串的离婚事件像多米诺骨牌一般接踵而至。若在Bi和Gi离婚的前提下，这2n个人最终依然能够结合成n对情侣，那么我们称婚姻i为不安全的，否则婚姻i就是安全的。

给定所需信息，你的任务是判断每对婚姻是否安全。

思路：我们做个约定，夫妻从妻子向丈夫连一条边，初恋则从男方连一条边到女方。连边结束后，我们构建出来了一张图，对图进行缩点，若某夫妻所在的强联通分量不一样则输出，一样则输出

代码：

#include 
using namespace std;
const int N=25000;
const int M=8100;
struct node{
	int next,to;
}e[N];int h[M],tot;
inline void add_edge_in_e(int a,int b){
	e[++tot]=(node){h[a],b};h[a]=tot;
}
//建图，注意是有向图
int dfn[N],low[N],dfscnt;
int Stack[N],stack_top;
int belong[N],dfscol;
void tarjan(int u){
	low[u]=dfn[u]=++dfscnt;
    //给每个节点一个dfs序
	Stack[++stack_top]=u;
	for(int i=h[u];i;i=e[i].next){
		register int v=e[i].to;
		if (!dfn[v]){
			tarjan(v);
			low[u]=min(low[u],low[v]);
		}
		else if (!belong[v])
		low[u]=min(low[u],dfn[v]);
	}
    //别把u和v写反了啊！
	if (low[u]==dfn[u]){
		belong[u]=++dfscol;
		while (Stack[stack_top]!=u){
			int v=Stack[stack_top];
			belong[v]=dfscol;--stack_top;
		}
		--stack_top;//注意这一句哦！
	}
}
//Tarjan缩点的模板，最好理解，不行就背！
map a;
string boy,gril;
int n,m,i;
int main(){
	cin>>n;
	for(i=1;i<=n;i++){
		cin>>gril>>boy;
		a[gril]=i;a[boy]=i+n;
        //利用map对字符串进行编号（c++ STL 真好！）
		add_edge_in_e(i,i+n);
	}
	cin>>m;
	for(i=1;i<=m;i++){
		cin>>gril>>boy;
		add_edge_in_e(a[boy],a[gril]);
        //别连反了啊
	}
	for(i=1;i<=n*2;i++)
	if (!dfn[i]) tarjan(i);
	for(i=1;i<=n;i++){
		if (belong[i]!=belong[i+n])
		printf("Safe\n");
		else printf("Unsafe\n");
	}
	return 0;
}

洛谷P2704：

题意：

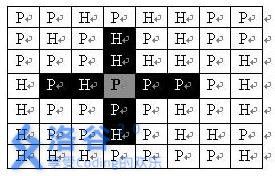
司令部的将军们打算在N*M的网格地图上部署他们的炮兵部队。一个N*M的地图由N行M列组成，地图的每一格可能是山地（用“H” 表示），也可能是平原（用“P”表示），如下图。在每一格平原地形上最多可以布置一支炮兵部队（山地上不能够部署炮兵部队）；一支炮兵部队在地图上的攻击范围如图中黑色区域所示：

如果在地图中的灰色所标识的平原上部署一支炮兵部队，则图中的黑色的网格表示它能够攻击到的区域：沿横向左右各两格，沿纵向上下各两格。图上其它白色网格均攻击不到。从图上可见炮兵的攻击范围不受地形的影响。 现在，将军们规划如何部署炮兵部队，在防止误伤的前提下（保证任何两支炮兵部队之间不能互相攻击，即任何一支炮兵部队都不在其他支炮兵部队的攻击范围内），在整个地图区域内最多能够摆放多少我军的炮兵部队？

思路：看到m这么小（），所以肯定是状压dp。首先计算出每行所有的可能情况（就是m取到最大值，这一行的所有格子都是平地，状态数也才不到70个！设f[i][j][k]表示处理第i行，第i行状态为j，第i-1行状态为k，转移如代码（太长了，不想写！）

代码：

#include 
using namespace std;
const int N=80;
struct node{
	int val[N],a[N],num;
}st[110];
int f[110][N][N],t,n,m;
inline void get_state(int v,int t){
	for(int i=0;i<(1<>1)||i&(i>>2)) continue;
		//啊，要自己人打自己人了，赶紧删除状态
		register int x=0,j;
		for(j=1;j<=m;j++)
		if (i&(1<>n>>m;ans=-100;
	for(i=1;i<=n;i++){
		t=0;
		for(j=1;j<=m;j++){
			cin>>ch;
			if (ch=='P') t*=2;
			else t=t*2+1;
		}
		get_state(i,t);
	}
	for(j=1;j<=st[1].num;j++)
	f[1][j][0]=st[1].val[j];
	for(i=1;i<=st[1].num;i++)
	for(k=1;k<=st[2].num;k++)
	if (pd(1,i,2,k))
	f[2][k][i]=st[1].val[i]+st[2].val[k];
	//边界
	for(i=3;i<=n;i++)
	for(j=1;j<=st[i].num;j++)
	for(k=1;k<=st[i-1].num;k++)
	for(l=1;l<=st[i-2].num;l++)
	if (pd(i,j,i-1,k)&&pd(i,j,i-2,l)&&pd(i-1,k,i-2,l))
	f[i][j][k]=max(f[i][j][k],f[i-1][k][l]+st[i].val[j]);
	//转移
	for(i=1;i<=st[n-1].num;i++)
	for(l=1;l<=st[n].num;l++)
	if (pd(n-1,i,n,l))
	ans=max(ans,f[n][l][i]);
	//求解
	if (n==1){
		for(l=1;l<=st[1].num;l++)
		ans=max(ans,f[n][l][0]);
	}
	//特判
	cout<