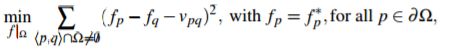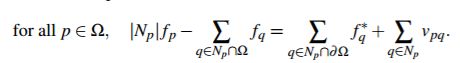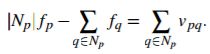泊松图像编辑(poisson Image Editing)
reference : 《poisson Image Editing》
概述
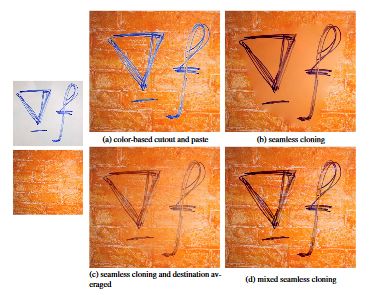
使用基于求解泊松方程的通用插值方法,我们可以引入多种无缝编辑图像区域的新工具。第一套工具可以将透明或者不透明的原图某一区域无缝拼接到目标区域上,第二套工具基于相似的数学原理,它支持用户无缝地修改指定区域内的图像的外观。这些变化可以在一定范围内的影响纹理、光照、特定区域颜色,或者让一个矩形区域重复平铺成更大的矩形区域。
介绍
图像编辑任务不仅要考虑全局的变化(颜色/强度矫正,滤波,变形),还要考虑某些选区的局部变化。在这里我们关注的是手动选择区域的局部变化。改变的内容涵盖了从轻微的扭曲到完全被新的东西替换。对于细微的变化而言,完成这一任务的经典工具包括了特定选区的图像滤波器;而对于完全替换的变化而言,有可交互式的复制粘贴克隆工具。使用这些经典的工具,只能隐藏部分选区内的缝隙,在选区边缘还有比较明显的痕迹。
我们在此提出了一种不同工具进行无缝编辑和选区复制的通用技术,这一方法的核心数学思想是具有Dirichlet边界条件的Poisson偏微分方程,它指定了感兴趣区域的未知函数的拉普拉斯算子,同时给出了函数域边界上的未知函数值。它的动机包含两部分。
首先,对大多数心理学家而言,他们认为拉普拉斯算子抑制下梯度变化较慢的强度可以叠加到图像不明显的地方。而与之相反的,拉普拉斯算子提取出的二阶变化才是最为重要的感知。
其次,有界区域上的标量函数是由它边界上的值和内部的拉普拉斯算子唯一确定的。Poisson方程因此有了唯一解,这也引出了一个完备的算法。
因此,给定构造某些域上未知函数的拉普拉斯算子,和它的边界条件的方法,Poisson方程就能解决无缝填充域的问题。对彩色图像来说这个过程可以在不同通道内分别重复。我们也可以把求解泊松方程理解为一个最小化问题:它对于给定边界条件的指定向量场如引导向量,计算在L2-范式下梯度最接近的函数。通过这样的方法,重建的函数向内插值边界条件,并保证引导域地空间变化尽可能接近。第二部分详细地介绍了这种引导插值(guided interpolation)
我们将会验证引导域下一系列可能的选择。需要特别指出的是,这些插值机制同时在易用性和性能方面改进了经典的克隆工具,克隆的结果允许用户无缝地添加或者移除物体。通过合理地混合原图像和目标图像的梯度,它也能够添加一些透明的对象。此外,有着复杂轮廓,包括洞的对象也能够自动地添加,而不需要人为的裁剪。这些不同的克隆功能将会在第三部分介绍。
在第四部分,我们使用同样的方法在特定区域修改图像的外观,并且避免边界的可见不连续部分。特别地,物体的颜色、纹理或者光照修改起来很方便,不需要边界部分精细的划分。同样,一个矩形图像区域能够无缝地平铺展开。
Poisson
在这一章节,我们将会详细介绍使用引导向量域进行图像插值的方法。我们可以对每个颜色分量独立的进行插值求解,因此我们可以仅仅考虑一个标量的颜色函数。图1解释了一些符号的含义:设图像定义域S为R^2上封闭子集合,![]() 是S的一个封闭子集,它的边界为
是S的一个封闭子集,它的边界为![]() 。令f*为定义在S上一个已知的标量函数,代表S减去
。令f*为定义在S上一个已知的标量函数,代表S减去![]() 的范围,令f为定义在
的范围,令f为定义在![]() 上一个未知的标量函数。最终,令v为定义在
上一个未知的标量函数。最终,令v为定义在![]() 上的向量域。
上的向量域。
定义在![]() 上f*的最简单的插值函数f:最小化问题的插值
上f*的最简单的插值函数f:最小化问题的插值
其中
其中![]() 是拉普拉斯算子。等式(2)是Dirichlet边界条件下的拉普拉斯方程。对于图像编辑应用而言,这一简单的方法可能有不尽人意的结果,模糊的插值效果,但可以有很多方法来克服。一种是使用更加复杂的偏微分方程([Bertalmio et al. 2000]中的修补技术)。在这里我们给出的建议是引入更多引导域上的约束来修改这一问题。
是拉普拉斯算子。等式(2)是Dirichlet边界条件下的拉普拉斯方程。对于图像编辑应用而言,这一简单的方法可能有不尽人意的结果,模糊的插值效果,但可以有很多方法来克服。一种是使用更加复杂的偏微分方程([Bertalmio et al. 2000]中的修补技术)。在这里我们给出的建议是引入更多引导域上的约束来修改这一问题。
一个引导域是最小化问题(1)的扩展版本中使用的向量域v:
它的解是Dirichlet边界条件下泊松方程的唯一解:
其中![]() 是v= (u,v)的散度。泊松图像编辑的基本机制是:在选中的颜色空间中,三个颜色通道各自对应一个如(4)中的泊松方程。这篇论文中的所有结果都是包含RGB颜色空间的。
是v= (u,v)的散度。泊松图像编辑的基本机制是:在选中的颜色空间中,三个颜色通道各自对应一个如(4)中的泊松方程。这篇论文中的所有结果都是包含RGB颜色空间的。
当引导域v是保守场时,比如,某些函数g的梯度,一个有用的替代方案是理解泊松插值所做的是定义![]() 上修正的
上修正的![]() 函数,以保证
函数,以保证![]() 。
。
泊松方程(4)随之成为了以下有边界条件的拉普拉斯方程:
因此,在![]() 内,我们添加的修正
内,我们添加的修正![]() 是就是边界
是就是边界![]() 上源和目标错误匹配(f*-g)的一个插值(membrance interpolant)。这一引导插值的特例被用于第三部分的无缝克隆。
上源和目标错误匹配(f*-g)的一个插值(membrance interpolant)。这一引导插值的特例被用于第三部分的无缝克隆。
离散泊松求解
变分问题(3)和相关的Dirichlet边界条件(4)下的泊松方程,可以有多种方法来求解。
对于离散图像而言,我们可以很自然地使用底层离散的像素网格。不失一般性,在离散对象中我们可以和连续物体相同的符号,S和![]() 现在代表的是定义无限离散网格上 的有限的点集合。注意到S可以包括一张图像的所有像素,或者只包含它的一个子集。对于S中的每个像素p,令
现在代表的是定义无限离散网格上 的有限的点集合。注意到S可以包括一张图像的所有像素,或者只包含它的一个子集。对于S中的每个像素p,令![]() 为S中的四邻域像素点的集合,定义像素对为(p,q),其中q为
为S中的四邻域像素点的集合,定义像素对为(p,q),其中q为![]() 中一个元素。现在
中一个元素。现在![]() 的边界为
的边界为![]() 令
令![]() 为f在像素p处的值。我们的任务是计算出强度的集合
为f在像素p处的值。我们的任务是计算出强度的集合![]()
对于定义在任意形状上的Dirichlet边界条件,最好直接求解变分问题(3),而不是计算泊松方程(4)。(3)的有限差分离散化后产生如下离散、二次优化的问题:
其中![]() 是
是![]() 在边[p,q]方向的投影。
在边[p,q]方向的投影。![]() 。它的解满足以下线性方程组:
。它的解满足以下线性方程组:
在![]() 扩展到网格边界时,
扩展到网格边界时,![]() 包含了S边界的像素,这些像素点的邻域是不完整的,它们的|
包含了S边界的像素,这些像素点的邻域是不完整的,它们的|![]() |<4。注意到像素p是
|<4。注意到像素p是![]() 内部的,也就是说,
内部的,也就是说,![]() 。也就是(7)的右方并没有边界,写作:
。也就是(7)的右方并没有边界,写作:
方程(7)形成了一个经典,稀疏(带状),对称的正定系统。因为边界的形状是任意的,我们必须采取交互式方案。
无缝克隆
引入梯度
引导域v的基本选择是原图像的梯度域。设原图像为g,那么引导域下的插值形式如下:
![]() (9)
(9)
现在方程(4)写作:
![]() (10)
(10)
而对于数值形式而言,(9)可以表达为:
![]() (11)
(11)
它可以被附加到(7)上。
无缝克隆工具因此确保了原图像和目标图像边界的一致性。它可以用于隐藏图像中不希望的部分,或者是插入新的元素。相比传统的技术更加灵活,也更加易用。
通过无缝引入背景/完整物体/部分物体的片段,一些不希望的特征能很容易就隐藏。
从用户输入的角度来考虑,大多数任务只需要比较模糊的套索选择,如下图。
但是,当原图像需要很好地匹配目标图像的特征的话,源和目标的特征需要更加精确。
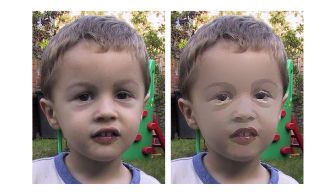
最后,在无缝克隆牵涉到大量纹理片段时,如图2中的脸部以及图4中的纹理交换,使用更广泛的画笔描边是更好的方法。
插值过程引起全局的变化后,原图像全部内容得以保存。在一些情况下,我们只希望保留原图像部分内容。这个问题最常见的现象是转移原图像的强度模式,而不是颜色。一个简单的解决方法是提前把原图像变成单色图像,如图5.
梯度混合
依据前一章节中描述的工具,![]() 中没有维护图像f*的信息。但是,在有些情况下我们需要结合f*和g的性质。例如,有时候我们会添加一个有洞的对象,或者在纹理或杂乱的背景上部分透明的物体。
中没有维护图像f*的信息。但是,在有些情况下我们需要结合f*和g的性质。例如,有时候我们会添加一个有洞的对象,或者在纹理或杂乱的背景上部分透明的物体。
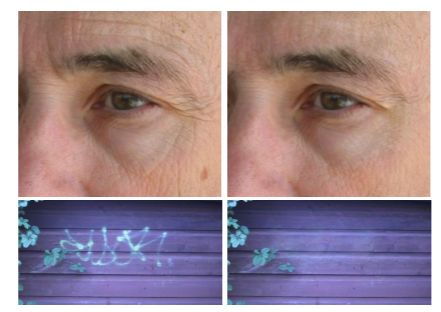
图6展示了一个例子,我们要把原图中的文本层剥离,添加到新的图像中去,而不需要复杂的选择操作。一个可能的途径是定义一个原图像和目标图像的线性结合的引导域,但是这会把原图中的纹理变得模糊。
不过,poisson方法支持使用非保守域,这就可能做出更好的效果。在![]() 中的每个点,我们根据如下引导域,保留了f*或g中更大的变量。
中的每个点,我们根据如下引导域,保留了f*或g中更大的变量。
选择编辑
在前两个章节中,引导域部分或完全地取决于原图像g的梯度。另外,直接对图像进行变换可以使用完全基于原图像的引导域。基于这个想法,这一张主要讲述纹理平滑、空间选择性改变光照,背景或前景颜色的修改。
纹理平滑
图像梯度![]() 通过一个只保留最显著特征的稀疏滤波:
通过一个只保留最显著特征的稀疏滤波:
![]() (14)
(14)
其中M是一个感兴趣区域上的二值矩阵。
M的一个比较好的选择是边缘探测器,(14)中的离散式子,带入(7)中,得到:
对于所有(p,q),如图9中所示,选区![]() 的内容更加平滑,小的细节被冲刷掉了,而基本的纹理被保留了。这一结果的效果取决于矩阵的稀疏程度。边界的选区越准确,边缘越稀疏。
的内容更加平滑,小的细节被冲刷掉了,而基本的纹理被保留了。这一结果的效果取决于矩阵的稀疏程度。边界的选区越准确,边缘越稀疏。
这个Poisson编辑的实例是强连通的,不同的是,我们通过稀疏引导(14)近似的估计边缘的梯度向量,这一系统依赖于每个边缘像素两边特定的颜色值。
局部光照变化
正如作者所说,[Fattal et al. 2002]中的方法不仅仅局限于HDR的图像,也能应用到普通的图像上,进行动态范围平滑。首先,对图像梯度域进行对数转换以降低高梯度并提升小梯度。然后我们使用变换向量域v,在整个图像域诺伊曼边界条件下,求解泊松方程![]() ,来重建图像的对数f。
,来重建图像的对数f。
一个很自然的拓展是使用![]() 上合适的Dirichlet条件,限制选区
上合适的Dirichlet条件,限制选区![]() 的校正。使用Fattal et al.的简化版,变换后的[Fattal et al. 2002],引导域可以定义在对数域上:
的校正。使用Fattal et al.的简化版,变换后的[Fattal et al. 2002],引导域可以定义在对数域上:
![]() (16)
(16)
其中,选区![]() 上f*的平均梯度下,
上f*的平均梯度下,![]()
![]()
正如图10所示,这一工具可以用于校正曝光不足的区域,或者将少镜面反射。
局部颜色改变
泊松编辑也是改变颜色的一个有力工具。给定一张原始颜色的图像和选中的区域![]() ,这个图像的两种颜色的版本可以无缝地混合:一个版本提供了
,这个图像的两种颜色的版本可以无缝地混合:一个版本提供了![]() 区域外地目标函数f*,另外一个提供了原函数g,可以根据(10)在
区域外地目标函数f*,另外一个提供了原函数g,可以根据(10)在![]() 内进行修改。
内进行修改。
例如,为了把图像中除了感兴趣物体外的区域都变成单色,传统的做法事精确地选择物体的边界(抠图),然后其余部分填充为单色。相反地,泊松编辑使人们从枯燥地选出精确的边界区域工作中解放出来:给定原来的彩色图像g,(a) 目标图像f*是图像g的亮度通道 (b)用户选择一个包含物体的区域![]() ,这个区域通常会比实际的物体大一些,(c)在每个颜色通道求解泊松方程(10)。
,这个区域通常会比实际的物体大一些,(c)在每个颜色通道求解泊松方程(10)。
图11给出了一个例子。注意到,虽然结果看起来精确地分割了对象,但实际上并不是。目标图像的对象之外仍然有一些残留的部分。
相反地,泊松图像编辑可以用于修改大致框选的物体的颜色。在求解泊松方程(10)之前,原图被复制到目的图像f*上,而修改了颜色的版本又复制到了源图像上,如图11。
无缝拼接
当区域是矩形时,我们可以通过求解泊松方程,得到周期边界条件,拼接它的内容。源图像g是原始图像,边界条件由g的边界值得到,所以除矩形区域外的部分对应着相同的Dirichlet条件。在图12中,我们同样也对对东边和西边的边界选定
![]()
结论
使用一般的引导插值框架,我们引入了不少无缝编辑和自动图片内容编辑的工具。可能的变化包括图像区域的替换,混合、原始图像特定区域属性的改变,例如纹理,光照或者颜色。这些工具的一个重要的通用特性是:我们不需要像传统的方法那样,对物体进行精确的划分。这是一个很有用的特性,无论在对图像做小的修改还是对复杂照片的拼接。
虽然文章中没有明确指出,但显而易见的是,章节3中描述的克隆技术和章节4中描述的编辑技术可以结合起来。例如,我们可以在图像中插入一个对象,并平滑它的纹理,使得它能和纹理不显著的目标匹配。
最终,值得注意的是,这篇文章同一框架下编辑工具的范围可以扩展。例如表面的改变也能用于感兴趣物体区域的锐利度修改,从而允许用户让焦点发生显著变化。