深入浅出Python机器学习7——支持向量机SVM
| 支持向量机SVM的基本概念 |
- 支持向量机SVM的基本原理
当数据线性不可分时,增加数据的维度,将其投射至高维空间,从而引出了SVM。
在SVM中用的最普遍的两种把数据投射到高维空间的方法是多项式内核(Ploynomial)和径向基内核(Radial basis function kernel,RBF)。其中多项是内核比较容易理解,它是通过把原始特征进行乘方来把数据投射到高维空间,比如特征1乘2次方、特征2乘三次方,特征3乘5次方等。而 RBF 内核也被称为高斯内核(Gaussian kernel),下面主要介绍的也是RBF。
- 支持向量机SVM的核函数
在SVM算法中,训练模型的过程实际上时对每个数据点对于数据分类决定边界的重要性进行判断。也就是说,在训练数据集中,只有一部分数据对于边界的确定是有帮助的,而这些数据点就是正好位于决定边界上的点。这些数据被称为“支持向量(support vectors)”,这也就是 “ 支持向量机 ” 名字的由来。
如下例中图所示。
可以看到,在分类器两侧分别有两条虚线,那些正好压在虚线上的数据点,就是我们刚刚提到的支持向量。而本例使用的这种方法称为 “ 最大边界隔离超平面(Maximum Margin Separating Hyperplane)”。指的是说中间这条实线(在高维数据中的一个超平面),和所有支持向量之间的距离,都是最大的。
将 SVM 的内核换成 RBF,看看如下结果。
发现分类器的样子变得完全不一样了,这是因为当我们使用RBF内核的时候,数据点之间的距离是用如下公式来计算的:
k r b f ( x 1 , x 2 ) = e x p ( γ ∣ ∣ x 1 − x 2 ∣ ∣ 2 ) k_{rbf}(x_1, x_2)=exp(\gamma||x_1-x_2||^2) krbf(x1,x2)=exp(γ∣∣x1−x2∣∣2)
公式中的 x 1 x_1 x1和 x 2 x_2 x2代表两个不同的数据点,而 ∣ ∣ x 1 − x 2 ∣ ∣ ||x_1-x_2|| ∣∣x1−x2∣∣ 代表两个点之间的欧氏距离, γ \gamma γ是用来控制RBF内核宽度的参数,也就是图中实线距离两条虚线的距离。
| SVM的核函数与参数选择 |
- 不同核函数的SVM对比
之前提到过一个 linearSVM 的算法,实际上 linearSVM 就是一种使用了线性内核的SVM算法。不过 linearSVM 不支持对核函数进行修改,因为它默认只能使用线性内核。
下面我们看看用不同内核的 SVM 算法在分类中的表现。


从图中我们可以看到,线性内核的 SVC 与 linearSVC 的到的结果十分相似,仍然有一点差别。其中一个原因是 linearSVC 对 L2 范数进行最小化,而线性内核的 SVC 是对 L1范数进行最小化。不论如何,linearSVC 和线性内核的 SVC 生成的决定边界都是线性的,在更高维数据集中将会是相交的平面。而 RBF 内核的 SVC 和 polynomial 内核的 SVC 分类器的决定边界完全不是线性的,它们更加有弹性。而决定了它们决定边界的形状的就是它们的参数。在 polynomial 内核的 SVC 中,起决定性作用的参数就是 degree 和正则化参数 C,在此例中 degree = 3 ,也就是说对原始数据集的特征进行乘3次方操作。而在 RBF 内核的 SVC 中,起决定性作用的是正则化参数 C 和 gamma。
- 支持向量机的gamma参数调节
下面我们来看看 RBF 内核 SVC 的 gamma 参数调节。

从图中我们发现,当 gamma 越小,RBF 内核的直径越大,这样就会有更多的点被模型圈进决定边界中,所以决定边界也就越平滑,这是模型也就越简单;而随着参数的增加,模型则更倾向于把每一个点都放到相应的决定边界中,这时模型的复杂度也就相应提高了。所以 gamma 值越小,模型倾向于欠拟合,而 gamma 值越大,模型更倾向于过拟合。
由第四篇我们知道,正则化参数 C 越小,模型就越受限, 也就是说单个数据点对模型的影响越小,模型就越简单;而 C 值越大,每个数据点对模型的影响就越大,模型也会更加复杂。
- SVM算法的优势和不足
SVM 可以说时在 ML 领域非常强大的算法,对各种不同类型的数据集都有不错的表现。它可以在数据特征很少的情况下生成非常复杂的决定边界,当然特征数量很多的情况下表现也不错,换句话说,SVM 应对高维数据集和低维数据集都还算时得心应手。但是,前提条件时数据集的规模不太大。如果数据集中的样本数量在 1 万以内, SVM 都能驾驭得了,但是如果样本数量超过 10 万的话,SVM 就会非常耗费时间和内存。
SVM 还有一个短板,就是对数据预处理和参数调节要求非常高。所以现在很多场景下大家都会更乐意用我们之前提到的随机森林算法或者梯度上升决策树(GBDT)算法。因为他们不需要对数据进行预处理,也不用费心去调参。而且对非专业人士来说,随机森林和梯度上升决策树要比SVM更容易理解,毕竟 SVM 算法的建模过程是比较难以呈现的。
不管怎么说,SVM 还是有价值的。假设数据集中样本特征的测度都比较接近,例如在图像识别领域,还有样本特征数和样本数比较接近的时候,SVM 都游刃有余。
在 SVM 算法中有 3 个参数是比较重要的:第一个是核函数的选择;第二个是核函数的参数,例如 RBF 的 gamma 值;第三个是正则化参数 C。RBF 内核的 gamma 值是用来调节内核宽度的,gamma 值和 C 值一起控制模型的复杂度,数值越大模型越复杂, 而数值越小模型越简单。实际应用中,gamma 值和 C 值往往要一起调节,才能达到最好的效果。
| SVM实例——波士顿房价回归分析 |
- 初步了解数据集
首先看一下数据集的大致情况,

波士顿房价数据集包含四个键,分别是数据、目标、特征名称和短描述。
相比于酒的数据集,波士顿房价数据集少了一个目标名称(target_names)键,看看数据描述。
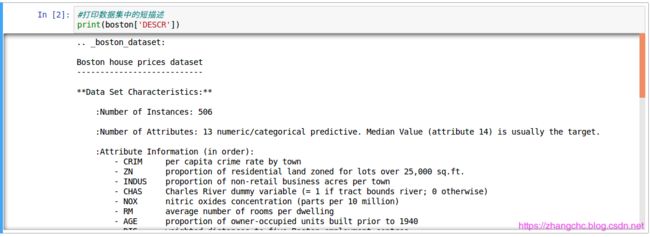
我们可以看出,数据集中有 506 个样本,每个样本有 13 个特征变量。而后面还有个叫作中位数的第 14 个变量,这个变量就是该数据集中的 target。如果继续往下看会发现,原来这个变量是业主自住房屋的价格的中位数,以千美元为单位。难怪将其作为target。接下来任务就是通过 SVR 算法,建立一个房价预测模型。
- 使用 SVR 进行建模
对于SVM算法,我们首先导入 sklearn.svm 中的 SVR 模块。SVR() 就是 SVM 算法来做回归用的方法(即输入标签是连续值的时候要用的方法)。
首先制作训练数据集和测试数据集,

已拆好训练数据集和测试数据集,然后我们选择 SVM 的核函数:“ Linear ” 和 “ rbf ” ,不过不知道哪个效果会更好,所以分别试一试。

从结果中我们发现,两种核函数的模型得分都不令人满意。
相比之下 “ rbf ” 的结果让人害怕,这会不会是数据集的各个特征之间量级相差的比较远引起的?在前面提到过,SVM 算法对于数据预处理的要求是比较高的,如果数据特征量级差异较大,我们就需要对数据进行预处理。所以我们先用图形看看数据集中各个特征的数量级的情况。

从结果看出,各个特征的数量级差异还是比较大的,第一个特征 “ 城市犯罪率 ” 最小值的在 1 0 − 2 10^{-2} 10−2, 而最大值达到了 1 0 2 10^{2} 102(这很可能是一个错误的数据点,犯罪率应该不会如此之高)。而第十个特征 “ 税收 ”的最小值和最大值都在 10 到 1 0 2 10^{2} 102之间。
为了让 SVM 更好的对数据进行拟合,我们必须对数据集进行预处理。如下所示:
可以看出,经过预处理之后,训练集和测试集基本上所有特征最大值都不会超过 10,最小值也都趋于 0,以至于在图中看不到它们了。
用经过预处理的数据来训练模型,看看有何变化:

经过预处理后 “ linear ” 得分变化不大,而 “ rbf ” 得分有了显著的提升,而且非常接近 “ linear ” 的效果。
进一步调整 “ linear ” 内核的 SVR 模型的参数 gamma 和 C。

当 C = 100 ,gamma = 0.1 时,我们发现 “ rbf ” 内核的 SVR 模型在训练集上的得分达到了 0.966,而在测试数据集上的得分也达到了 0.894,模型的表现时可接受的。
通过对数据进行预处理和对参数的调节,使得 “ rbf ” 内核的 SVR 模型在测试集中的得分从 0.001 升到了 0.894,通过这个案例,可以清晰的了解到 SVM 算法对于数据预处理和调参的要求都是非常高的。


