深入浅出Python机器学习9——数据预处理、降维、特征提取及聚类
| 数据预处理 |
- 使用 StandScaler 进行数据预处理
首先手工生成一些数据:
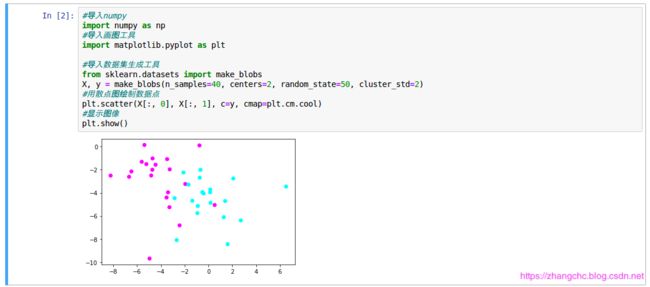
用make_blobs 函数时,指定了样本数量 n_samples 为 40,分类 centers 为 2,随机状态 random_state 为 50,标准差 cluster_std 为 2.从图中可以看出数据集中样本有 2 个特征,分别对应 x 轴和 y 轴,特征 1 的数值大约在 -8 ~ 7之间,特征 2 的数值大约在 -10 ~ 10 之间。
用 StandardScaler 对数据预处理:
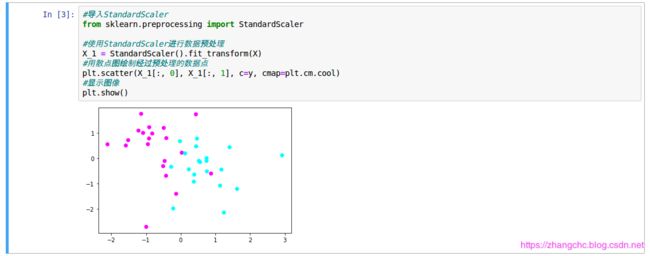
从图中可以看出,数据点分布没变化,但是数值进行了缩放。这是因为, StandardScaler 的原理时,将所有数据的特征值转换为均值为 0,而方差为 1 的状态,这样可以确保数据的 “ 大小 ” 都是一致的,这样更有利于模型的训练。
- 使用 MinMaxScaler 进行数据预处理
直接进入示例:

从图中发现,特征值都被转换到了 0 ~ 1 之间。这也有利于模型训练的速度更快且准确率提高。
- 使用 RobustScaler 进行数据预处理
RobustScaler 和 StandardScaler 比较相似,但是它并不是用均值和方差来进行转换,而是使用中位数和四分位数。这种方法会直接把一些异常值踢出去,例如将最高分和最低分剔除。
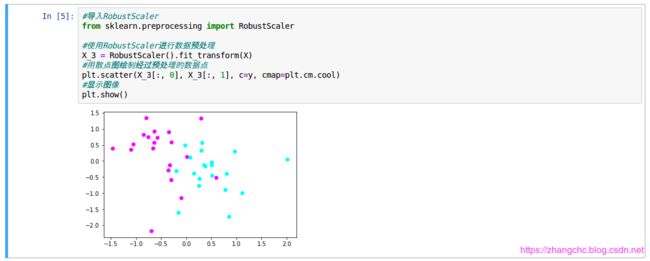
从图中发现,特征值的范围得到控制。和 StandardScaler 非常相似,但原理不同从而结果也有所不同。
- 使用 Normalizer 进行数据预处理
Normalizer 将所有样本的特征向量转化为欧几里得距离为 1。也就是说,它把数据的分布变成一个半径为 1 的圆,或者是一个球。这种方法通常我们是只想保留数据特征向量的方向,而忽略其数值的时候使用。
在图像来展示 Normalizer 的工作方式:

可以看出,数据点分布在了一个圆上。
- 通过数据预处理提高模型准确率
为了说明数据预处理的意义,我们用酒的数据集测试一下:

结果表明,训练集有 133 个样本,测试集有 45 个样本,而且均有 13 个特征。
用数据集来训练一个 MLP 神经网络,

可以看到没有进行预处理的情况下,模型得分只有 0.93。接着对数据预处理:

可以看到,得分显著提升到了 1.0,也就是说预处理后的 MLP 神经网络在测试数据集中进行了完美的分类。
注意:预处理在拟合前进行预处理才有意义,拟合后再处理就失去了数据转换的意义。
| 数据降维 |
- PCA 主成分分析原理
主成分分析法(Principlal Compontent,PCA)是提取主要特征,将一些无关紧要的特征剔除,让数据从高维变为低维。
-
对数据降维以便于进行可视化
导入数据并打印数据信息:

从图中可以看到,样本数量为 178,特征数量是 13,接下来用 PCA 处理数据:

注意:因为 PCA 主成分分析法属于无监督学习算法,所以这里只对 X_scaled 进行了拟合,而没有涉及分类标签 y。
可以看出,样本数量是 178 没变,但是特征数量变为了 2。
进一步对 PCA 降维的数据可视化:


为了可视化砍掉了其余 11 个特征,不科学。但是用 PCA 将数据集的特征向量降至二维,从而轻松进行可视化处理,同时又不会丢失太多的信息。 -
原始特征与 PCA 主成分之间的关系
想要知道原来 13 个特征和经过 PCA 处理的得到的 2 个特征之间的关系,从数学的角度,大家要继续了解内积和投影。这里通过画图,我们来理解一下。
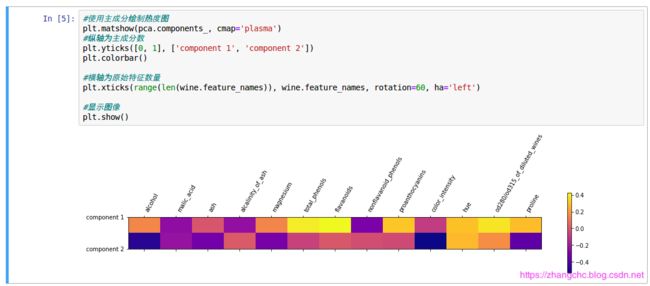
在图中,颜色有深入浅代表一个从 -0.5 ~ 0.4 的数值。而在两个主成分中,分别涉及了所有的 13 个特征。如果某个特征对应的数字是正数,说明它和主成分是正相关的关系,如果是负数则相反。
在 scikit-learn 中,PCA 的 n_components 不仅可以代表成分的个数,还可以设置为降维之后保留信息的百分比,例如我们希望降维之后保留原特征 90% 的信息,那么就设置 n_components 为 0.9。
| 特征提取 |
有时候我们对数据集原来的特征进行转换,生成新的 “ 特征 ” 或者说成分,会比直接使用原始的特征效果更好。这里我们引进一个新的名词,称为 “ 数据表达 ”(data representation)。
在数据集极为复杂的情况下,比如图像识别,数据表达就显得十分重要。因为图像是有成千上万个像素组成,每个像素上又有不同的 RGB 色彩值,所以我们要用到一个新的数据处理方法,称为 “ 特征提取 ”(feature extraction)。
- PCA 主成分分析法用于特征提取
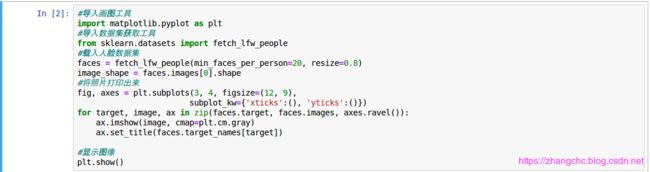
本次用到的 LFW 人脸识别数据集包含了若干张 JPEG 图片,是从网上搜集的一些名人的照片。每张照片都是一个人的脸部。而创建这个数据集的目的,是训练机器学习算法,看给出两个照片,算法是否能判断出这两个人是否是同一个人。后来又有新的要求:给出一张照片,判断这个人的名字。
首先看一下数据集:

接着我们再数据集未处理的情况下,训练神经网络:
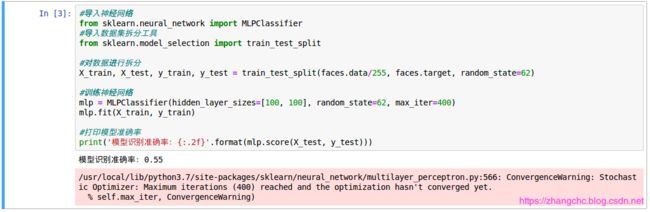
可以看出得分只有 0.55,也就是有将近一般的错误。
为了提升模型,接下来要用到的就是 PCA 主成分分析法中的数据白化功能(data whiten)。
所谓的白化功能,在这个例子中,虽然每个的面部特征有很大差异,但如果你从像素级别观察,差距其实就没有那么大了。而且相邻的像素之间有很大的相关性,这样一来,样本特征的输入就是冗余的了,白化的目的就是为了要降低冗余性。所以白化的过程会让样本特征之间的相关度降低,且所有特征具有相同的方差。
下面用 PCA 的白化功能处理一下 LWF 人脸数据集:

这里保留了原始特征中的 90% 的信息,所以参数 n_components 设置为 0.9。从图中可以看出经过 PCA 白化处理的数据成分为 105 个,远远小于原始数据的特征数量 87 x 65 = 5655 个。
接着看看白化后的神经网络识别的准确率如何:

可以看出,模型的准确率有了略微的提高 0.57,这就说明了 PCA 数据白化功能对于提高神经网络模型的准确率是有了一定帮助的。
- 非负矩阵分解用于特征提取
在 scikit-learn 还封装了非负矩阵分解(Non-Negative Matrix Factorization,NMF),NMF 也是一个无监督学习算法,同样可以用于数据的特征提取。
所谓矩阵分解就是把一个矩阵拆解为 n 个矩阵的乘积。而非负矩阵分解,就是原始的矩阵中所有的数值必须大于或等于 0,当然分解之后的矩阵中的数也是大于或等于 0 的。
与 PCA 不同的是,如果我们降低 NMF 的成分数量,它会重新生成新的成分,而新的成分和原来的成分是完全不一样的。另外,NMF 中成分是没有顺序的,这点和 PCA 也有所不同。下面用 NMF 对 LFW 人脸数据集进行特征提取,再重新训练神经网络。

注意:和 PCA 不同,NMF 的 n_components 参数不支持使用浮点数,只能设置为正的整型数。

从图中可以看出,NMF 处理后的数据训练的神经网络模型准确率和 PCA 处理后的模型准确率基本持平,略微低一点。
| 聚类算法 |
有监督学习主要用于分类和回归,而无监督学习的一个非常重要的用途就是对数据进行聚类。而聚类和分类有一定的相似之处,分类是算法基于已有标签的数据进行学习并对数据进行分类,而聚类则是在完全没有标签的情况下,有算法 “ 猜测 ” 哪些数据像是应该 “ 堆 ” 在一起的,并且让算法给不同的 “ 堆 ” 里的数据贴上一个数字标签。
- K均值聚类算法
K 均值聚类算法算是聚类中最简单的了,但是也是用的最多的算法。它的工作原理是这样的:假设我们的数据集中的样本因为特征不同,像小沙堆一样散布在地上,K 均值算法会在小沙堆插上旗子。而第一遍插的旗子并不能很完美地代表沙堆地分布,所以 K 均值还要继续, 让每个旗子能够插到每个沙堆最佳地位置上,也就是数据点的均值上,这也是 K 均值算法的名字的由来。接下来会一直重复上述的动作,直到找不出更好的位置。
下面用手工生成的数据集来展示一下 K 均值聚类算法原理:
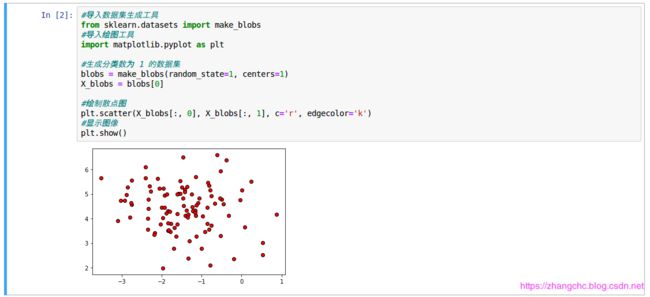
从图中可以看出,由于我们指定了 make_blobs 的center 参数为 1,因此所有的数据都属于 1 类,并无差别。
继续用 K 均值来帮助这些数据进行聚类:
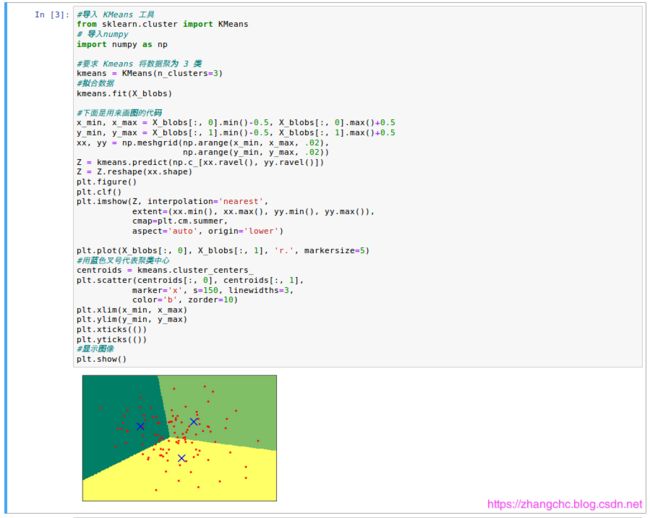
图中代码,设定 K 均值的 n_clusters 参数是 3,所以 K 均值将数据点聚为 3 类,图中的 3 个蓝色的 X 号,就代表了 K 均值堆数据进行聚类的 3 个中心。
接下来看看 K 均值怎么表示这些聚类:

可以看出,K 均值对数据进行的聚类和分类有些相似,是用 0、1、2 三个数字来代表数据的类,并且存储在.labels_属性中。
这反映了,K 均值算法十分简单而且容易理解,但是它也有很明显的局限性。例如,它认为每个数据点到聚类中心的方向都是同等重要的。这样的话,对于 “ 形状 ” 复杂的数据集来说,K 均值算法就不能很好的工作。
- 凝聚聚类算法上插旗子
实际上,凝聚聚类算法是一揽子算法的集合,而着一揽子算法的共同之处就是,它们首先将每个数据点看成一个聚类,然后把相似的聚类进行合并,直到达到停止的标准。如 scikit-learn 中,停止的标准就是聚类的数量。
用 K 聚类的数据集演示,如下图所示:

可以看出,凝聚聚类算法是自下而上,不断地合并相似地聚类中心,以便让类别越来越少,同时每个聚类中心地距离也就原来越远。这种逐渐生成地聚类方法称为 Hierarchy clustering。
和 K 均值聚类算法比较相似,凝聚聚类算法也无法对 “ 形状复杂 ” 的数据进行正确的分类。
- DBSCAN 算法
算法的全称是 “ 基于密度的有噪声应用空间聚类 ” (Density-based spacial clustering of applicantions with noise)。DBSCAN 是通过对特征空间内的密度进行检测,密度大的地方就会认为是一个类,而密度小的地方它会认为是一个分界线。也正是由于这样的工作机制,使得 DBSCAN 算法不需要像 K 均值或者是凝聚聚类算法那样在一开始就指定聚类的数量 n_clusters。
下面展示一下其运行机制:
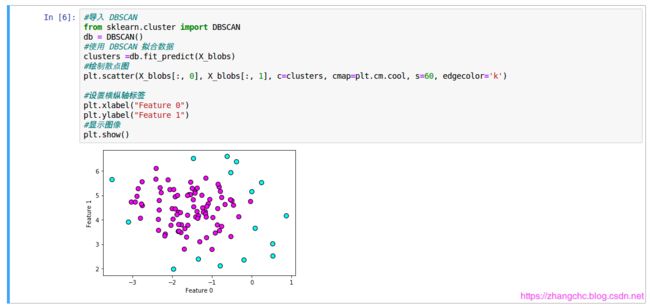
看出来,经过 DBSCAN 的聚类,数据点被标成了不同的深度。

相比之前的算法,聚类标签中出现了 ‘ -1 ’,这是由于在 DBSCAN 算法中 ‘ -1 ’ 代表的是噪声。 在前面分类图中可以发现深色的数据点密度相对较大,因此 DBSACN 将它们归为一类,而外围的浅色的数据点, DBSCAN 认为不属于任何一类,所以放到了噪声这一类。
DBSCAN 有两个非常重要的参数:一是 eps;一是 min_samples。 eps 指定的是考虑划入同一类的样本距离有多远,eps 越大,则聚类所覆盖的数据点越多,反之则越少。默认情况 eps=0.5。当 eps=2 时如下所示:
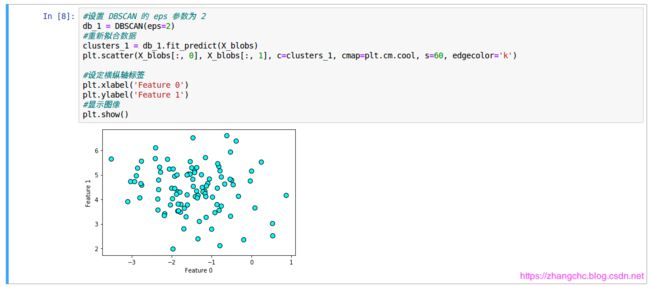
结果分析可以看出所有数据点都变成浅色了,这并不是所有的都为噪声,而是看出了同一类,因为增加了 eps 的取值后,让 DBSCAN 把距离更远的数据点也拉到了这个聚类中。
而 min_samples 参数指定的时在某个数据点周围,被看成聚类核心点的个数,min_samples 值越大,则核心数据点越少,噪声也就越多;反之 min_samples 值越小,噪声也就越少。默认的 min_samples 值是 2。如下所示:
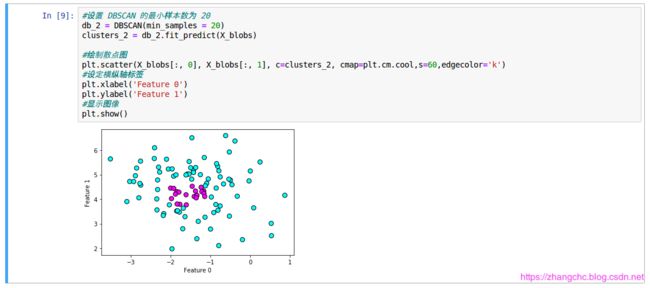
发现图中的浅色数据点变多了,也就是噪声变多了。而深色数据点变少了。
从上面分析看来,虽然 DBSCAN 不需要我们在开始训练算法的时候就指定 clusters 的 数量,但是通过对 eps 和 min_samples 参数赋值,相当于间接地指定了 cluters 的数量。尤其是 eps 参数尤为重要,因为它规定了这一坨数据的范围大小。而在实际应用中,如果将数据先用 MinMaxScaler 或者 StandardScaler 进行预处理,那么 DBSCAN 算法的表现会更好(因为这两种预处理方法把数据的范围控制得比较集中)。
对机器学习来说,能够合理有效地对数据进行表达至关重要。因此数据预处理、降维、特征提取在对数据进行准备工作地过程中起着非常关键的作用。而对于没有分类的标签数据来说,无监督学习的聚类算法可以帮助我们更好地理解数据集,并且为进一步训练模型打好基础。
小编机器学习学的一般,只是日常做做比记加深一下印象,望读者不吝赐教,谢谢!