深入浅出Python机器学习8——神经网络

神经网络的前世今生

       这一部分时对先驱们的致敬，若是不想看可以直接跳过。
       在1943年，美国神经解剖学家沃伦麦克洛奇（Warren McCulloch）神经网络和数学家沃尔特皮茨（Walter Pitts）就提出了一个脑神经元的抽象模型，被称为M-P 模型（McCulloch-Pitts neuron，MCP）。
       1958 年，著名的计算机科学家弗兰克罗森布拉特（Frank Rossenblatt）基于 M-P 模型提出了第一个感知机学习法则。
       1969 年，计算机领域的大牛马文明斯基（Marvin Minsky）出版preceptron的一书中，阐述了感知机的弱点，让神经网络的研究进入了低谷。
       又过了将近十年的时间，杰弗瑞欣顿（Geoffery Hinton）等人提出了反向传播算法（Back propagation，BP），解决了两层神经网络所需的复杂计算问题，重新带动业界的热潮。而他本人也被大家称为 “ 神经网络之父 ”。
       20世纪90年代中期，SVM 算法的出现显露出强悍的能力，例如不需要调参、效率更高等，它的出现有一次将神经网络击败，称为了当时的主流算法。从此神经网络又进入低谷时期。
       好在杰弗瑞欣顿并没有放弃，在神经网络摒弃的时间里，他和其他几个学者还坚持在研究，而且给多层神经网络算法起了一个新的名字——深度学习。
       再后来，深度学习占据了统治地位，不管是图像识别、语言识别、自然语言处理、无人驾驶等领域，都有非常广泛的应用。而本篇重点介绍的是神经网络当中的多层感知器（Multilayer Preceptron，MLP）。

神经网络的原理及使用

• 神经网络的原理

       MLP 也被称为前馈神经网络，或者被泛称为神经网络。回顾一下线性模型的一般公式：

$$\hat{y}=w[0]\cdot x[0]+w[1]\cdot x[1]+\cdots +w[p]\cdot x[p]+b$$
       这相当于一个单层感知机模型，而在 MLP 模型中，算法在过程中添加了隐藏层（Hidden Layers）,然后在隐藏层中继续加权求和计算，最后把隐藏层所计算的结果用来生成最终的结果。
       这样一来，模型要学习的特征系数，或者说权重，就会多很多。在每一个输入的特征和隐藏单元（hidden unit）之间，都有一个系数，这是为了生成这些隐藏单元。而每个隐藏单元到最终结果之间，也有一个系数。而计算一系列的加权求和和计算单一的加权求和。

• 神经网络中的非线性矫正

       从数学的角度来看，如果每个隐藏层只是进行加权求和，得到的结果和普通的线性模型不会有什么不同。所以为了让模型能够比普通线性模型更强大一些，在生成隐藏层之后，要对结果进行非线性矫正（rectifying nonlinearity），简称为 relu（rectified linear unit）或者是进行双曲正切矫正（tangens hyperbolicus），简称为 tanh。通过这两种方式处理后的结果用来计算最终结果 y。如下例：

       可以看出，tanh 函数是把特征 x 的值压缩进 -1~1 之间。relu 函数是把小于 0 的 x 值全部去掉，用 0 来代替。
       这样一来，经过 tanh 处理后原来的隐藏层式子就变成了：

$$h[0]=tanh(w[0]\cdot x[0]+w[1]\cdot x[1]+\cdots +w[p]\cdot x[p]+b)$$

$$\cdots$$

$$\hat{y}=v[0]\cdot h[0]+v[1]\cdot h[1]+\cdots +v[n]\cdot h[n]$$

       在权重系数 w 之外，又多了一个 v，用来通过隐藏层计算 y-hat 的结果。在模型中 w 和 v 都是通过对数据的学习所得出的。而用户所要设置的参数，就是隐藏层中节点的数量。一般来讲，对于小规模数据集或者简单数据集，节点数量设置为 10 就够了，但是对于大规模数据集或者复杂数据集来说，有两种方式可供选择：一是增加隐藏层中的节点数，比如增加到1万个；或者添加更多的隐藏层。
       在大型网络当中，往往有很多这样的隐藏层，这也是 “ 深度学习 ” 中 “ 深度 ” 二字的来源。

• 神经网络的参数设置

       以 MLP 分类器为例，首先导入酒的数据集：

       参数说明：
       activation 是将隐藏单元进行非线性化的方法，一共有4种：“ identity ” “ logistic ” “ tanh ” 和 “ relu ” ，在默认情况下，参数是 “ relu ” 。“ identity ” 对样本不做处理，返回$f(x)=x$。“ logistic ” 返回结果是$f(x)=1/[1+exp(-x)]$，这结果和 tanh 类似，在处理之后特征值会在 0~1 之间。
       alpha 值和线性模型的 alpha 值是一样的，是一个 L2 惩罚项，用来控制正则化的程度，默认的数值是 0.0001。
       hidden_layers_sizes 在默认下的值是 100，这意味模型中只有一个隐藏层，而隐藏层中的节点数是 100。如果我们给 hidden_layers_sizes 定义为[10, 10]，那就意味着有两个隐藏层，每个有 10 个节点。
       实例说明：

       将隐藏层节点减少至 10 ，

       我们发现，节点数为 10 的时候，决定边界丢失了很多细节。可以这样理解，在每个隐藏层中，节点数酒代表了决定边界中最大的直线数，这个值越大，则决定边界看起来越平滑。当然，除了增加单个隐藏层中的节点数之外，还有两种方法可以让决定边界更加细腻：一个是增加隐藏层的数量；另一个是把 activation 参数改为 tanh。
       如下例，MLP 增加到 2 层，每层 10 个节点。

       可以看出，边界更加细腻了，接着使用 activation = ‘ tanh ’ 测试。

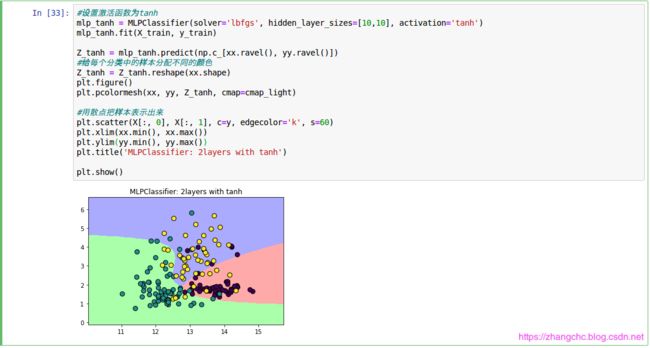
       可以看出，决定边界完全变成平滑的曲线，这就是对样本特征进行双曲线正切化后的结果。
       进一步，我们可以改变 alpha 值（默认是0.0001），

       可以看出，增加 alpha 参数的数值，会加大模型正则化的程度，也就是说模型会变得更简单。
       注意：由于神经网络算法中，样本特征的权重是在模型开始学习之前，就已经随机生成了，而随机生成的权重会导致模型的形态也完全不一样。所以我们不能指定 random_state 的话，即便模型所有参数都是相同的，生成的决定边界也不一样。所以如果重新运行前面的代码，也会的到不同的结果。不过只要模型的复杂度不变，其预测结果的准确率不会受到什么影响。

神经网络实例——手写识别

• 使用MMIST数据集

       MNIST数据集是一个专门用来训练各种图像处理系统的庞大数据集，它包含了 70000 个手写数字图像，其中 60000 个是训练数据， 另外 10000 个是测试数据。 而在机器学习领域，该数据集也被广泛用于模型的训练和测试。MNIST数据集实际上是NIST原始数据集中提取的，其训练集和测试集有一半是来自NIST数据集的训练集，而另一半是来自NIST的测试集。目前有大量的学术论文都在试图把模型对MNIST数据集的识别错误率不断降低，目前识别错误率最低的一篇论文使用的是卷积神经网络，成功地把错误率降低到了 0.23%。而最早创造这个数据集的学者，在他们最早的论文中使用了支持向量机算法，使模型识别的错误率达到 0.8%。
       下例使用了scikit-learn 的 fetch-mldata 来获取 MNIST数据集，

       从结果中看出，MNIST数据集包含两个部分：一个是数据的分类标签（label）；另一个是数据本身（data）。Data的类型是无符号的 8 位整型 np 数组，而 target 是从 0~9 的整形数组。
       看看数据集中的样本数量和样本特征数量。

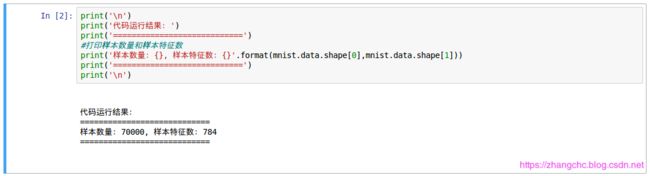
       可以看出，样本数量为 70000，每个样本有 784 个特征。这是因为数据集存储的样本是28x28像素的手写数字图片的像素信息，因此特征数量为 28x28=784个。
       在开始训练 MPL 神经网络之前，我们还需要将数据进行一些预处理，由于样本特征是从 0~255 的灰度值，为了让特征的数值更利于建模，我们把特征向量的值全部除以 255，这样全部数值就会在 0 ~ 1 之间，再用 train_test_split 函数将数据集拆分为训练集和测试集。
       进一步，为了控制神经网络的训练时长，我们只选 5000 个样本作为训练数据集，选取 1000 个数据作为测试数据集。同时为了每次选取的数据保持一致，我们指定 random_state 为 62。

• 训练 MLP 神经网络

       建立好数据集后，开始训练神经网络：

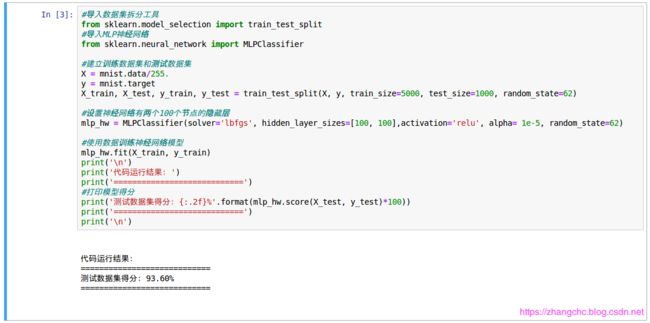
       从图中我们可以看到，模型在测试集中的识别准确率达到了93.6%，是一个不错的分数。

• 使用模型进行数字识别

       用下图进行测试，

       注意：图像为 28 x 28 像素.

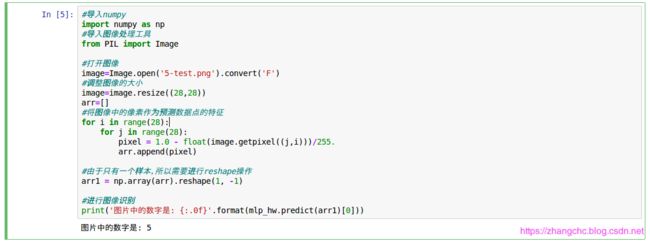
       注意调用了 python 内置的图像处理库 PIL, 为了让识别效果能达到最优，我们先用 Image.convert 功能将图片转化为 32 位浮点灰度图像，也就是说它的每个像素用 32 个 bit 来表示，0 代表黑，255 代表白。然后将每个像素的数值都进行除以 255 的处理，以保持数据集一致 。
注意：由于 MNIST 数据集是用 0 代表白色，1 代表黑色，因此我们还要用 1 减去像素的灰度值，以保持和数据集一致。
       此外由于只有一个样本，我们还要对其进行 reshape（1，-1）的操作，便可得到上图结果。

       后面可以进一步学习python里面的其它深度学习库，例如keras、theano 和 TensorFlow，其中keras可以使用 tensor-flow 和 theano作为后端（backend）。这些深度学习库都支持使用 CPU 加速，而 scikit-learn 并不支持。所以在处理超大数据集的时候，上面提到的几个深度学习库要比 scikit-learn 效率更高。待深度学习篇在继续介绍。
       小编机器学习学的一般，只是日常做做比记加深一下印象，望读者不吝赐教，谢谢！