Kaggle项目Digit Recognizer实现（二）：caffe by python

上篇文章使用cs231n提供的python代码，实现了一个三层卷积神经网络，用于kaggle项目Digit Recognizer。由于实现更复杂的神经网络完全手写代码较为繁琐，所以这里采用caffe重新实现，希望能提高识别准确率。
本文中caffe使用python借口调用，并在ipython notebook中运行，其中，代码编写参考了http://caffe.berkeleyvision.org/中的notebook example: Image Classification and Filter Visualization和Learning LeNet

csv文件写入LMDB

由于该项目中数据文件保存在csv文件中，而caffe中data层常用数据格式为LMDB（当然也有其他方式，这里仅给出LMDB），所以第一步先将csv文件写入LMDB。
与前一篇文章相同，将训练数据按9:1分为train和val部分，其中，csv文件读取与上篇文章相同，不过需将readCSVFile函数改为

def readCSVFile(file):
    rawData = []
    csvfile = open(file, 'rb')
    reader = csv.reader(csvfile)
    for line in reader:
        rawData.append(line)
    rawData.pop(0)#remove file header
    intData = np.array(rawData).astype(np.uint8)#此处数据类型修改，与下面LMDB写入统一
    csvfile.close() 
    return intData

数据读取后依次写入LMDB

from pylab import *
%matplotlib inline
caffe_root = '你的caffe路径' 
import sys
sys.path.insert(0, caffe_root + 'python')
import caffe
from readCSV import csv_data
import numpy as np
import lmdb

#读入csv数据，其中，训练数据分为两部分，train和val，后者为1000个
data = csv_data.get_mnist_data()
X_train = data['X_train']
y_train = data['y_train']
X_val = data['X_val']
y_val = data['y_val']
X_test = data['X_test']

#生成train_lmdb文件
N = size(X_train,axis = 0)
map_size = X_train.nbytes * 10
env = lmdb.open('train_lmdb', map_size=map_size)

with env.begin(write=True) as txn:
    # txn is a Transaction object
    for i in range(N):
        datum = caffe.proto.caffe_pb2.Datum()
        datum.channels = X_train.shape[1]
        datum.height = X_train.shape[2]
        datum.width = X_train.shape[3]
        datum.data = X_train[i].tobytes()  # or .tostring() if numpy < 1.9
        datum.label = int(y_train[i])
        str_id = '{:08}'.format(i)

        # The encode is only essential in Python 3
        txn.put(str_id.encode('ascii'), datum.SerializeToString())

#生成val_lmdb文件
N = size(X_val,axis = 0)
map_size = X_val.nbytes * 10

env = lmdb.open('val_lmdb', map_size=map_size)

with env.begin(write=True) as txn:
    # txn is a Transaction object
    for i in range(N):
        datum = caffe.proto.caffe_pb2.Datum()
        datum.channels = X_val.shape[1]
        datum.height = X_val.shape[2]
        datum.width = X_val.shape[3]
        datum.data = X_val[i].tobytes()  # or .tostring() if numpy < 1.9
        datum.label = int(y_val[i])
        str_id = '{:08}'.format(i)

        # The encode is only essential in Python 3
        txn.put(str_id.encode('ascii'), datum.SerializeToString())

生成train.prototxt,test.prototxt配置文件

lenet()用于生成网络，并将参数存入prototxt文件

#生成net
from caffe import layers as L, params as P
def lenet(lmdb, batch_size):
    # our version of LeNet: a series of linear and simple nonlinear transformations
    n = caffe.NetSpec()

    n.data, n.label = L.Data(batch_size=batch_size, backend=P.Data.LMDB, source=lmdb,
                             transform_param=dict(scale=1./255), ntop=2)

    n.conv1 = L.Convolution(n.data, kernel_size=5, num_output=20, weight_filler=dict(type='xavier'))
    n.pool1 = L.Pooling(n.conv1, kernel_size=2, stride=2, pool=P.Pooling.MAX)
    n.conv2 = L.Convolution(n.pool1, kernel_size=5, num_output=50, weight_filler=dict(type='xavier'))
    n.pool2 = L.Pooling(n.conv2, kernel_size=2, stride=2, pool=P.Pooling.MAX)
    n.fc1 =   L.InnerProduct(n.pool2, num_output=500, weight_filler=dict(type='xavier'))
    n.relu1 = L.ReLU(n.fc1, in_place=True)
    n.fc2 =   L.InnerProduct(n.relu1, num_output=500, weight_filler=dict(type='xavier'))
    n.relu2 = L.ReLU(n.fc2, in_place=True)
    n.score = L.InnerProduct(n.relu2, num_output=10, weight_filler=dict(type='xavier'))
    n.loss =  L.SoftmaxWithLoss(n.score, n.label)

    return n.to_proto()

with open('train.prototxt', 'w') as f:
    f.write(str(lenet('train_lmdb', 64)))
with open('test.prototxt', 'w') as f:
    f.write(str(lenet('val_lmdb', 100)))

生成solver文件

solver文件中保存训练过程中的参数

### define solver
from caffe.proto import caffe_pb2
s = caffe_pb2.SolverParameter()

# Set a seed for reproducible experiments:
# this controls for randomization in training.
#s.random_seed = 0xCAFFE

# Specify locations of the train and (maybe) test networks.
s.train_net = 'train.prototxt'
s.test_net.append('test.prototxt')
s.test_interval = 640  # 41000/64 = 640次训练,即一个epoch后测试一次
s.test_iter.append(10) # Test on 100 batches each time we test.

s.max_iter = 204800     # 最大训练次数,320epoch

# EDIT HERE to try different solvers
# solver types include "SGD", "Adam", and "Nesterov" among others.
s.type = "Adam"

# Set the initial learning rate for SGD.
s.base_lr = 0.0001  # EDIT HERE to try different learning rates
# Set momentum to accelerate learning by
# taking weighted average of current and previous updates.
s.momentum = 0.9
# Set weight decay to regularize and prevent overfitting
s.weight_decay = 5e-4

# Set `lr_policy` to define how the learning rate changes during training.
# This is the same policy as our default LeNet.
s.lr_policy = 'inv'
s.gamma = 0.0001
s.power = 0.75
# EDIT HERE to try the fixed rate (and compare with adaptive solvers)
# `fixed` is the simplest policy that keeps the learning rate constant.
# s.lr_policy = 'fixed'

# Display the current training loss and accuracy every 1000 iterations.
s.display = 100

# Snapshots are files used to store networks we've trained.
# We'll snapshot every 5K iterations -- twice during training.
s.snapshot = 100000
s.snapshot_prefix = 'custom_net'

# Train on the GPU
s.solver_mode = caffe_pb2.SolverParameter.GPU

# Write the solver to a temporary file and return its filename.
with open('solver.prototxt', 'w') as f:
    f.write(str(s))

训练网络

caffe的python接口提供solve函数，可以自动完成训练并保存模型和训练过程。

### load the solver and create train and test nets
caffe.set_device(0)
caffe.set_mode_gpu()
solver = None  
solver = caffe.get_solver('solver.prototxt')
solver.solve()

也可以利用step函数进行单步训练，这种方法的好处是便于根据自己的需要，在训练过程中进行其他处理。例如此处保存loss和val数据集的测试准确率，并画出曲线。

caffe.set_device(0)
caffe.set_mode_gpu()
solver = None  # ignore this workaround for lmdb data (can't instantiate two solvers on the same data)
solver = caffe.get_solver('solver.prototxt')
### solve
niter = 204800  # EDIT HERE increase to train for longer
test_interval = 640
# losses will also be stored in the log
train_loss = zeros(niter)
test_acc = zeros(int(np.ceil(niter / test_interval)))

# the main solver loop
for it in range(niter):
    solver.step(1)  # SGD by Caffe

    # store the train loss
    train_loss[it] = solver.net.blobs['loss'].data

    if it % 100 == 0:
        print 'Iteration', it, 'loss = ', train_loss[it]
    # run a full test every so often
    # (Caffe can also do this for us and write to a log, but we show here
    #  how to do it directly in Python, where more complicated things are easier.)
    if it % test_interval == 0:

        correct = 0
        for test_it in range(10):
            solver.test_nets[0].forward()
            correct += sum(solver.test_nets[0].blobs['score'].data.argmax(1)
                           == solver.test_nets[0].blobs['label'].data)
        test_acc[it // test_interval] = correct / 1e3
        print 'Iteration', it, 'testing... test_acc = ', test_acc[it // test_interval]

solver.net.save('mymodel_204800.caffemodel')#保存模型
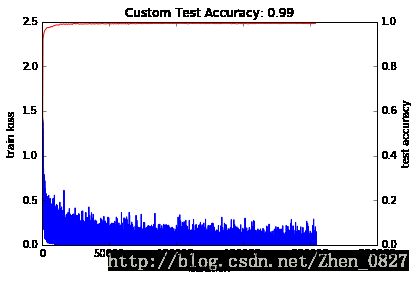
_, ax1 = subplots()
ax2 = ax1.twinx()
ax1.plot(arange(niter), train_loss)
ax2.plot(test_interval * arange(len(test_acc)), test_acc, 'r')
ax1.set_xlabel('iteration')
ax1.set_ylabel('train loss')
ax2.set_ylabel('test accuracy')
ax2.set_title('Custom Test Accuracy: {:.2f}'.format(test_acc[-1]))

绘制曲线如下

生成测试结果

生成deploy文件

利用caffemodel模型进行预测，需要先生成deploy.prototxt文件。该文件与train.prototxt类似，需要修改的地方为输入层（无label），以及最后的输出（softmax)

#生成deploy
def create_deploy():
    # our version of LeNet: a series of linear and simple nonlinear transformations
    n = caffe.NetSpec()
    n.data = L.Input()#需手动修改deploy文件input_layer输入维数

    n.conv1 = L.Convolution(n.data, kernel_size=5, num_output=20, weight_filler=dict(type='xavier'))
    n.relu1 = L.ReLU(n.conv1, in_place=True)
    n.pool1 = L.Pooling(n.relu1, kernel_size=2, stride=2, pool=P.Pooling.MAX)

    n.conv2 = L.Convolution(n.pool1, kernel_size=5, num_output=50, weight_filler=dict(type='xavier'))
    n.relu2 = L.ReLU(n.conv2, in_place=True)
    n.pool2 = L.Pooling(n.relu2, kernel_size=2, stride=2, pool=P.Pooling.MAX)

    n.conv3 = L.Convolution(n.pool2, kernel_size=4, num_output=120, weight_filler=dict(type='xavier'))
    n.dropout3 = L.Dropout(n.conv3, dropout_ratio = 0.5)
    n.relu3 = L.ReLU(n.dropout3, in_place=True)

    n.fc4 =   L.InnerProduct(n.relu3, num_output=84, weight_filler=dict(type='xavier'))
    n.dropout4 = L.Dropout(n.fc4, dropout_ratio = 0.5)
    n.relu4 = L.ReLU(n.dropout4, in_place=True)

    n.score = L.InnerProduct(n.relu4, num_output=10, weight_filler=dict(type='xavier'))
    n.prob = L.Softmax(n.score)
    return n.to_proto()

with open('deploy.prototxt', 'w') as f:
    f.write(str(create_deploy()))

生成deploy.prototxt文件后，打开该文件，再输入层加入输入数据维数信息（暂时没搞清楚如何在input层定义时写入该参数，只好麻烦一下手写了○|￣|_）

layer {
  name: "data"
  type: "Input"
  top: "data"
  input_param { shape: { dim: 1 dim: 1 dim: 28 dim: 28 } }
}

对前十个手写数字进行识别

model_def = 'deploy.prototxt'
model_weights = 'mymodel_204800.caffemodel'

net = caffe.Net(model_def,      # defines the structure of the model
                model_weights,  # contains the trained weights
                caffe.TEST)     # use test mode (e.g., don't perform dropout)
#设置输入大小，如果只需1幅图也可以不设置
net.blobs['data'].reshape(10,        # batch size
                          1,         # 1-channel images
                          28, 28)  # image size is 28x28
image = X_test[:10,:]/255.0
# copy the image data into the memory allocated for the net
net.blobs['data'].data[...] = image
### perform classification
output = net.forward()

output_prob = output['prob'][:10,:]  # the output probability vector for the first image in the batch

print 'predicted class is:', output_prob.argmax(axis=1)
plt.imshow(image[:,0,:,:].transpose(1,0,2).reshape(28,28*10), cmap='gray')

预测输出为

predicted class is: [2 0 9 9 3 7 0 3 0 3]

可以看到，第四个数字’0’被识别为了0，模型还需要进一步优化（模型结构或训练次数及参数）

生成预测结果csv文件

与上篇文章类似，每次预测100幅图片，并将结果写入csv文件，提交到kaggle后，测试准确率为0.99114。比上次的三层网络有一定提高，但准确率仍不太理想。