Scikit-Learn 集成方法（Ensemble method） 学习

集成算法的目标是：组合几个基学习器的预测，以此来提高单个模型的泛化性和健壮性

集成方法常分为两类：

1. averging methods：平均法的原则是： 独立的构建几个学习器，然后平均他们的预测。通常，组合的学习器要比任何一个单个的学习器要好，因为它降低了方差。   其中的代表：bagging 方法，随即森林
2. boosting methods：学习器依次构建，试图降低组合的学习器的偏差。                                                                                                                                           其中的代表：AdaBoost，Gradient Tree Boosting

1、 Bagging

在集成算法中，bagging方法在原始数据集的基础之上利用黑盒的方式构建几个学习器，然后将它们独立的预测进行聚集，作为最后的预测。

通过在基学习器构建的过程中引入随机方法，并最后通过集成。利用这种方式来降低单个学习器的方差。

若是希望通过一种方式来降低overfitting：

1. baggnig方法，在模型strong、complex的时候效果好
2. boosting方法，在模型weak的时候效果好

Bagging方法有很多形式，不同的是随机选择训练数据的方式

1. 随机选择数据子集--->Pasting
2. 可以重复抽样--->Bagging
3. 样本在随机选择的属性中抽样-- Random Subspaces
4. 构建基学习器的时候样本和属性都是子集时---> Random Patches

2、随机森林

在Scikit-Learn的ensemble模块中有两个平均的方法基于决策树：随机森林（RandomForest）和极限树（Extra-Trees）。

一个小例子：

from sklearn.ensemble import RandomForestClassifier    
X = [[0, 0], [1, 1]]    
Y = [0, 1]    
clf = RandomForestClassifier(n_estimators=10)    
clf = clf.fit(X, Y) 

2.1 随机森林

在随机森林（包括随机森林分类和随机森林回归），每一棵树都是通过又放回的抽样的方式获得的。并且每棵树的节点在分裂时选择特征子集（随机特征子集）中最好的特征进行分裂节点。

依靠这种方式随机森林的偏差可能会增加，但是方差会降低。

2.2 Extremely Randomized Trees 极限树

在极限随机树种（包括极限树分类和极限树回归），在分裂节点时，随机的更彻底一些。跟随机森林算法一样，极限树算法会随ijide选择特征子集，不同的是：会在每个特征中随机的选择阈值来划分特征，而不是寻找最佳的划分阈值。然后在这里边选择最好的作为划分特征和划分特征的阈值。

由于随机的更加彻底，方差会进一步降低，凡是偏差会增大。

一个小例子：

from sklearn.model_selection import cross_val_score
from sklearn.datasets import make_blobs
from sklearn.ensemble import RandomForestClassifier
from sklearn.ensemble import ExtraTreesClassifier
from sklearn.tree import DecisionTreeClassifier

X, y = make_blobs(n_samples=10000, n_features=10, centers=100,random_state=0)

clf = DecisionTreeClassifier(max_depth=None, min_samples_split=2,random_state=0)
scores = cross_val_score(clf, X, y)
scores.mean()                           

clf = RandomForestClassifier(n_estimators=10, max_depth=None,min_samples_split=2, random_state=0)
scores = cross_val_score(clf,X,y)
scores.mean()                             

clf = ExtraTreesClassifier(n_estimators=10, max_depth=None,min_samples_split=2, random_state=0)
scores = cross_val_score(clf,X,y)
scores.mean() > 0.999

2.3 参数

最主要的参数有两个n_estimators、 max_features

n_estimators: 代表森林中树的数量。越多越好，但是越多代表着训练时间越长。

max_features ： 当划分一个节点时可以考虑的特征子集的大小。 越小越能降低方差，但是越会增加偏差

2.4 特征重要性评估

可以利用feature_importances_ 获得特征的重要性

3、 AdaBoost

AdaBoost的关键：通过顺序的学习一些弱分类器（这些 弱分类器仅比随机好一点），然后通过加权投票得到最后的预测。

 每一次迭代样本的权重都回更新，初始时wi=1/n

一个小例子：

from sklearn.model_selection
import cross_val_scorefrom sklearn.datasets import load_iris
from sklearn.ensemble import AdaBoostClassifier

iris = load_iris()
clf = AdaBoostClassifier(n_estimators=100)
scores = cross_val_score(clf, iris.data, iris.target)
scores.mean()   

 4、Gradient Tree Boosting

GBRT的优点：

1. 可以处理异类特征(特征的类型不一样)
2. 准确的预测能力
3. 对异常点具有鲁棒性

缺点：

1. 由于它是顺序依次构建每一棵树，所以很难并行

4.1 分类

GradientBoostingClassifier能够支持二分类和多分类。

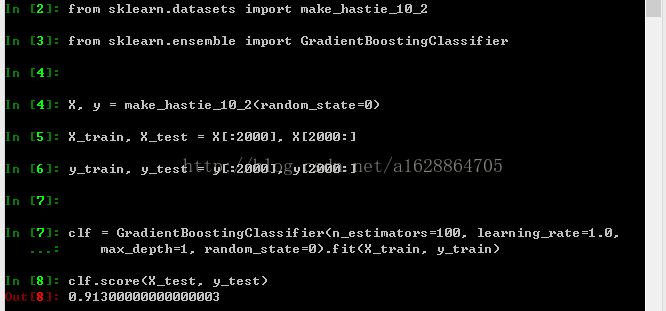
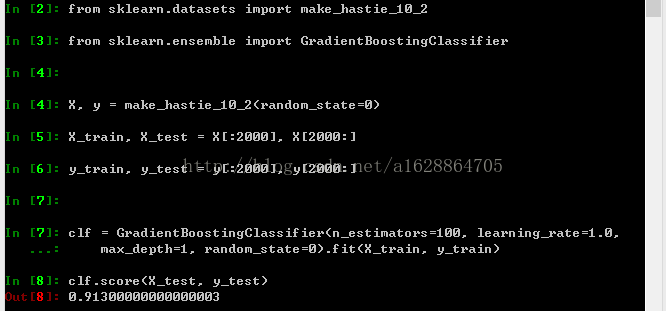
一个小例子：

from sklearn.datasets import make_hastie_10_2
from sklearn.ensemble import GradientBoostingClassifier

X, y = make_hastie_10_2(random_state=0)
X_train, X_test = X[:2000], X[2000:]
y_train, y_test = y[:2000], y[2000:]

clf = GradientBoostingClassifier(n_estimators=100, learning_rate=1.0,
    max_depth=1, random_state=0).fit(X_train, y_train)
clf.score(X_test, y_test)

4.2回归

GradientBoostingRegressor 支持不同的loss function，可以通过loss 关键字来进行修改，默认的loss function 是least squares（‘ls’）.

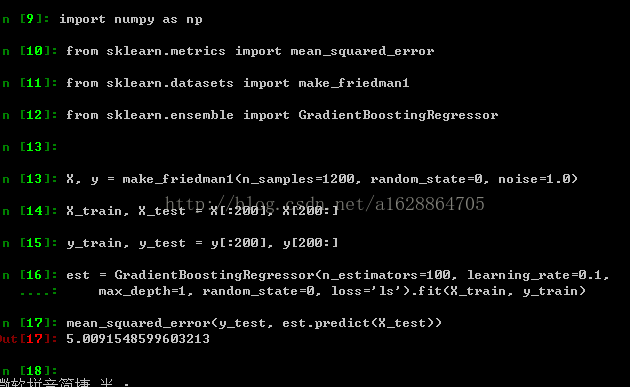
一个小例子：

import numpy as np
from sklearn.metrics import mean_squared_error
from sklearn.datasets import make_friedman1
from sklearn.ensemble import GradientBoostingRegressor

X, y = make_friedman1(n_samples=1200, random_state=0, noise=1.0)
X_train, X_test = X[:200], X[200:]
y_train, y_test = y[:200], y[200:]
est = GradientBoostingRegressor(n_estimators=100, learning_rate=0.1,
    max_depth=1, random_state=0, loss='ls').fit(X_train, y_train)
mean_squared_error(y_test, est.predict(X_test))

4.5 loss functions

可以通过loss参数来修改损失函数：

对于回归来说：

1. ls 
2. lad
3. huber
4. quantile

对于分类来说：

1. deviance
2. expoential

4.6 Regularizatoin  正则

4.6.1  Shrinkage

通过参数v来控制每个弱学习贡献，参数v也就做学习率因为它能够控制梯度下降过程每一步的大小。可以通过learning_rate参数来调节大小。

4.6.2 subsampling

在每一次迭代中，每一个基学习器通过训练数据集的二次抽样来构建，注意：抽样不是又放回的，一般设置为0.5 （样本数的一半）

4.7 解释

单棵决策树通过可视化可以非常容易的解释，但是在Gradient boosting 模型中，有上百棵树，将几百棵树通过可视化的方式进行解释比较困难。但是有其他的一下方法可以用来summarize 和interpret Gradient boosting模型。

4.7.1 Feature importance

不同的特征在预测一个结果是其发挥的作用是不一样的，在多数情况下，很多特征是没有用的。

可以通过feature_importances_ 属性可以得到Gradient Boosting 模型中属性的重要程度

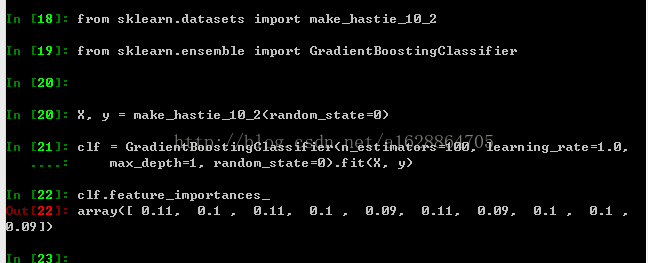
一个小例子：

from sklearn.datasets import make_hastie_10_2
from sklearn.ensemble import GradientBoostingClassifier

X, y = make_hastie_10_2(random_state=0)
clf = GradientBoostingClassifier(n_estimators=100, learning_rate=1.0,
    max_depth=1, random_state=0).fit(X, y)
clf.feature_importances_

4.7.2 Partial dependence

Partial dependence  可以表现目标和一个特征自己的依赖关系（忽略其他特征的取值）。直观上来说，我们可以解释Partial dependence ：目标是特征的的函数

5、VotingClassifier

votingClassifier的基本思想是：组合不同的机器学习模型，通过投票或者是平均的方式预测最后的标签。

5.1 Majority Class Labels (Majority/Hard Voting)

多数投票，一个预测样本的标签有每个分类器预测标签的大多数决定。

例如：

给定一个样本，有三个分类器

- classifier 1 -> class 1

- classifier 2 -> class 1

- classifier 3 -> class 2

这个样本就会被预测为class1

若是出现平局的情况：

- classifier 1 -> class 2

- classifier 2 -> class 1

VotingClassifier 会把预测标签升序排列，在本例中样本就会被预测为class1

一个小例子：

>>> from sklearn import datasets
>>> from sklearn.model_selection import cross_val_score
>>> from sklearn.linear_model import LogisticRegression
>>> from sklearn.naive_bayes import GaussianNB
>>> from sklearn.ensemble import RandomForestClassifier
>>> from sklearn.ensemble import VotingClassifier

>>> iris = datasets.load_iris()
>>> X, y = iris.data[:, 1:3], iris.target

>>> clf1 = LogisticRegression(random_state=1)
>>> clf2 = RandomForestClassifier(random_state=1)
>>> clf3 = GaussianNB()

>>> eclf = VotingClassifier(estimators=[('lr', clf1), ('rf', clf2), ('gnb', clf3)], voting='hard')

>>> for clf, label in zip([clf1, clf2, clf3, eclf], ['Logistic Regression', 'Random Forest', 'naive Bayes', 'Ensemble']):
...     scores = cross_val_score(clf, X, y, cv=5, scoring='accuracy')
...     print("Accuracy: %0.2f (+/- %0.2f) [%s]" % (scores.mean(), scores.std(), label))
Accuracy: 0.90 (+/- 0.05) [Logistic Regression]
Accuracy: 0.93 (+/- 0.05) [Random Forest]
Accuracy: 0.91 (+/- 0.04) [naive Bayes]
Accuracy: 0.95 (+/- 0.05) [Ensemble]

5.2 Weighted Average Probabilities (Soft Voting)概率加权平均

硬投票的反面

例子： 设有3个类，3个分类器，每个分类器的权重为  w1=1, w2=1, w3=1.

classifier	class 1	class 2	class 3
classifier 1	w1 * 0.2	w1 * 0.5	w1 * 0.3
classifier 2	w2 * 0.6	w2 * 0.3	w2 * 0.1
classifier 3	w3 * 0.3	w3 * 0.4	w3 * 0.3
weighted average	0.37	0.4	0.23

最后会选择calss2 作为最后的预测结果