朴素贝叶斯分类器——机器学习算法（二）

自从 AlphaGo 掀人工智能的巨大热潮之后，我便对人工智能产生了极大的兴趣。在人工智能各种算法面前，我有一种深深的无力感，一边在网络上了解TensorFlow、Caffe等大公司开源的框架，一边重新翻阅温习高数、概率的知识，一边死磕入门书籍中如决策树、神经网络、深度学习等等概念，就是为了有朝一日能踏上人工智能的大船，向着未来杨帆。

我记得老师说过：“在八、九十年代，有很多科学家都在研究人工智能，希望能实现图灵测试，让计算机能拥有人的智慧。但是多年的发展，人工智能从符号机器学习到统计机器学习，从数学的角度看，从离散变为连续、从代数和逻辑到概率和统计，机器也只是在计算方面变得更强，并没有成为真正的人工智能。” 如今，大数据似乎带来了机遇，通过数理统计的方式也许会让计算机有了思考的能力。

在机器学习的各种算法中，对于我来说，除了决策树之外，并在现有数学掌握程度来看，朴素贝叶斯分类器应该最容易理解的算法之一了。所以我是根据自己的理解来写这篇文章。本文分三个部分，一、回顾贝叶斯公式；二、朴素贝叶斯分类器原理；三、朴素贝叶斯分类器的应用。这三个部分都为理论部分，在下一篇文章，我会解释怎么用代码来实现朴素贝叶斯分类器。

一、回顾贝叶斯公式

如果不知道贝叶斯公式是什么的，可以参考我上一篇文章：http://blog.csdn.net/a727911438/article/details/55847696。

在这里我再简单提一下贝叶斯公式的计算方法，作为下文的铺垫。

假设小明自己开发了一个简单的电商网站，用来卖书的。这个网站很奇怪，只有一个搜索栏和下拉选项，用户只能在搜索栏输入关键字和下拉选择某项（只有编程、传记、经营三项）然后搜索店面是否有对于关键字的书籍。在本文中，这个店面有什么书您甭管，仅举例而已。

从上面的假设来看，用户的搜索有两个维度（特征），一个是关键字，一个是类型。

今天店主小明做了如下统计，统计用户提交的搜索：

问：假设今天有一个新用户，他搜索关键字为软件工程，那么选择经营类的可能性有多少？

解：

以上仅简单回顾，以下正式进入主题。

二、朴素贝叶斯分类器原理

假设店主小明无聊没事做，自己折腾通过搜索量统计出来关键字的受欢迎程度，并加入到统计表中：

从表中来看，统计了搜索的两个维度（特征）+ 一个分类（热门、冷门）。

这个时候，问：关键字=软件工程、类型=编程 的书籍是否热门？

计算方式为：根据贝叶斯公式，得：

再问：关键字=软件工程、类型=编程 的书籍冷门的概率？

计算方式为：根据贝叶斯公式，得：

计算结果很明显，{冷门}=1，{热门}=0。经过比较，{冷门} > {热门}，所以关键字=软件工程、类型=编程的书籍肯定是冷门的。

上面又简单讲了一遍普通的贝叶斯公式，那么，朴素贝叶斯究竟跟普通贝叶斯有什么不一样？？？答：朴素贝叶斯，关键在于朴素两个字，顾名思义，简朴、简单。意思就是：普通贝叶斯的精简版。

为了更好地理解朴素贝叶斯，我们先来看看上面式子的分子。

红圈圈住的部分 P（软件工程×编程 | 冷门） 这个式子特别难算，照着表来算还好，但是万一表格的数据特别特别多，那就计算到头都要爆炸了。

所以，需要将式子简化一下，让程序更容易编写和加快计算机的计算速度。于是，假设所有特征都彼此独立（即关键字、类型两个特征的概率相互独立，至于相互独立是什么概念，请自行学习概率论），那么分子部分可变为：

------------------------------------------------------------------------------------------------------------------------

如果多个特征之间并非相互独立，即关键字、类型这两个特征非独立，那么以上式子结果为 ≈约等于。不过有数学家证明过，误差不大。所以，尽情地把特征当成相互独立的吧！

难道朴素贝叶斯就只是假设所有特征都彼此独立，然后改一下分子吗？ 并非这么简单！

先来回顾以下，判断 关键字=软件工程、类型=编程 的书籍是否热门，最终要将两条式子求得的结果{冷门} 和 {热门} 对比一下，哪个值更大，哪个就是所求结果。敏感的少年可能又要问了，为什么要对比一下？ 在上面例子的类别中，只有冷门、热门两种受欢迎程度，非常直观，直觉上哪个大于二分之一答案就是哪个。可是，如果将类别扩充一下，有“大热门”、“热门”、“一般”、“冷门”、“大冷门” 这五种受欢迎程度时，有可能在已知特征的情况下，五个类别的最终概率都差不多，这个时候就要通过比较，选择最大值的那个。比如：猜猜 关键字=Linux、类别为编程 的书籍的热门程度，假设求得的结果为 {大热门}=0.19、{热门}=0.21、{一般}=0.25、{冷门}=0.20、{大冷门}=0.15，因为 {一般} 的值最大，所以可知热门程度为一般。

这个时候回归到小学数学题，两个分数比较，分母相同，分子越大的数越大。根据这一原理，再来观察上面两个式子，就会发现，两个式子的分母是相同的，而最终结果是通过比较两个式子的大小求得，所以更进一步，朴素贝叶斯连分母都可以不要了。于是就有（分子已做改变）：

上图两个式子就是精简后的贝叶斯公式，常称朴素贝叶斯。那么在机器学习领域中为什么称之为朴素贝叶斯分类器？ 根据例子，通过已知关键字、类型来求受欢迎程度，实际上就是，已知多个特征求类别。特征可以有很多很多个，如除了“关键字”、“类型”，还可以有“建议读者年龄”、“书籍价格区间”等等；类别也可以多个，受欢迎程度如上述的“大热门”、“热门”、“一般”、“冷门”、“大冷门”等等。那么朴素贝叶斯分类器的意思是根据特征来分类。（加粗这句是我自己的理解，如果有误请欢迎反馈）

以上就是我所理解的朴素贝叶斯分类器的原理。我自认所讲述的比其他文章和教材更加通俗易懂，但是不够深度。所以，要完全理解什么是朴素贝叶斯分类器，单单本篇文章是不够的，还需要掌握严谨的数学表示方式等，请自行某度更多文章配合理解。

三、怎么应用朴素贝叶斯分类器

说实话，朴素贝叶斯分类器的应用我还在学习中，所以我准备将在下一篇文章实现朴素贝叶斯分类器的代码。在那之前，我在网上找了一些思路，朴素贝叶斯分类器的应用大概分为3步：

1、收集、整理数据：

这一步主要是收集并整理大量数据，轻量级的有通过调查问卷收集信息，重量级的有从数据库中拷贝所需的数据。不管是轻量级还是重量级，最终的数据都要生成一个利于程序编写遍历的格式。

2、训练数据：

将上一步所得的数据进行统计，计算已知各类别的条件下各特征的概率，并作记录保存。这一步称为训练。

3、投入使用：

将上一步训练完成所得的大量概率用于产品中，根据用户所需来动态计算出结果。

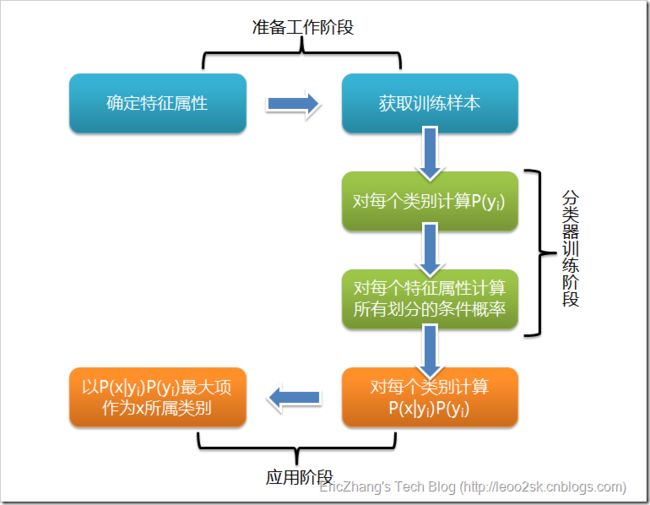
以上三步可用下面这张图概括：

为什么贝叶斯这么简单的公式能用于人工智能？是因为当数据量越来越大，用贝叶斯求出的概率就越准确，意味着计算机就越聪明。其实人类的思考方式跟贝叶斯公式差不多，当某个人经验积累足够时，对事物的判断就更加贴近本质，就像一个经验丰富的医生，通过症状就能快速的诊断疾病。当计算机把人类产生的所有数据都学习了一遍，那么计算机就比所有人都聪明了。

基于贝叶斯公式的算法还有很多，除了朴素贝叶斯分类器，还有半朴素分类器、贝叶斯网、EM算法等等（参考于周志华《机器学习》）。所以，要学习的还很多很多。如果志同道合的你看完了这篇文章，希望对本文错谬之处多多指点，不胜感谢，也希望我们一起学习、一起进步。