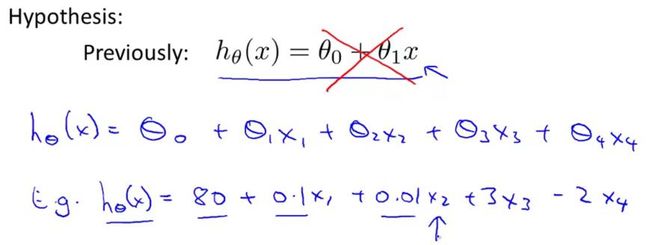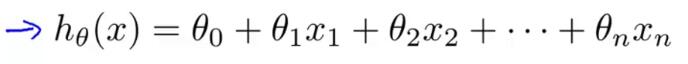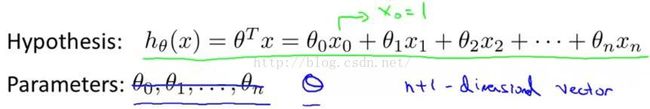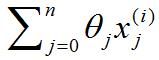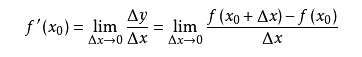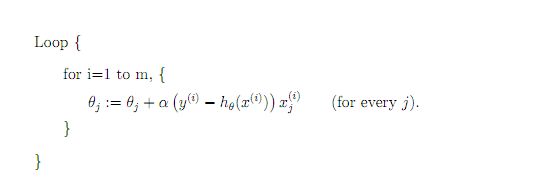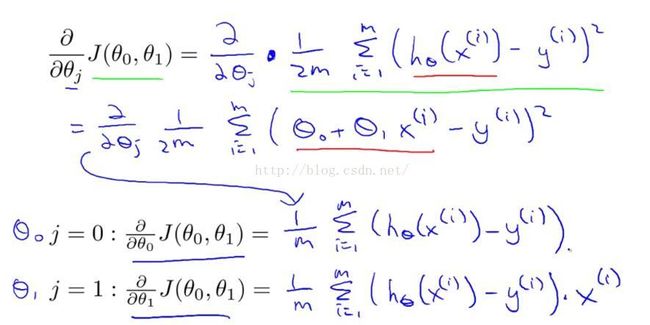Machine Learning(Stanford)| 斯坦福大学机(吴恩达)器学习笔记【汇总】
from:https://blog.csdn.net/m399498400/article/details/52556168
定义本课程常用符号
训练数据:机器用来学习的数据
测试数据:用来考察机器学习效果的数据,相当于考试。
m = 训练样本的数量(训练集的个数)
x = 输入的特征(例如房屋面积)
y = 输出结果(例如房屋售价)
(x(i),y(i)) = 表示训练集中第i个训练样本
一.Cost Function(代价函数)
一,什么是代价函数
我在网上找了很长时间代价函数的定义,但是准确定义并没有,我理解的代价函数就是用于找到最优解的目的函数,这也是代价函数的作用。
二,代价函数作用原理
对于回归问题,我们需要求出代价函数来求解最优解,常用的是平方误差代价函数。
里面有θ0和θ1两个参数,参数的改变将会导致假设函数的变化,比如: 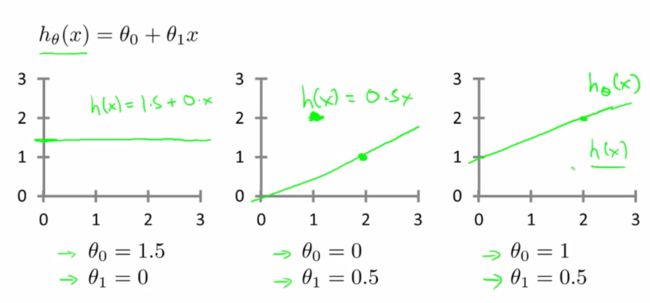
现实的例子中,数据会以很多点的形式给我们,我们想要解决回归问题,就需要将这些点拟合成一条直线,找到最优的θ0和θ1来使这条直线更能代表所有数据。 
而如何找到最优解呢,这就需要使用代价函数来求解了,以平方误差代价函数为例。
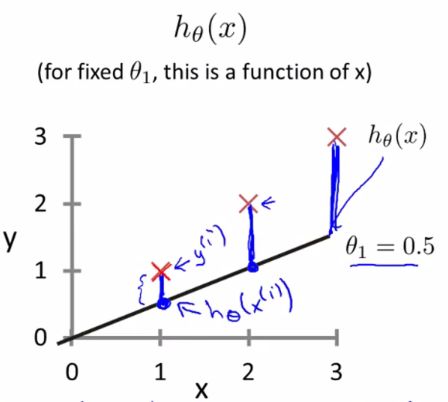
从最简单的单一参数来看,假设函数为: 
平方误差代价函数的主要思想就是将实际数据给出的值(x(i),y(i))与我们拟合出的线的对应值做差,这样就能求出我们拟合出的直线与实际的差距了。
为了使这个值不受个别极端数据影响而产生巨大波动,采用类似方差再取二分之一的方式来减小个别数据的影响。这样,就产生了代价函数:
【平均数: ![]() (n表示这组数据个数,x1、x2、x3……xn表示这组数据具体数值)
(n表示这组数据个数,x1、x2、x3……xn表示这组数据具体数值)
【拟合出的线的对应值—实际数据给出的值(x(i),y(i))】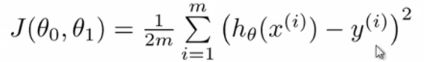
而最优解即为代价函数的最小值,根据以上公式多次计算可得到
代价函数的图像: 
可以看到该代价函数的确有最小值,这里恰好是横坐标为1的时候。
如果更多参数的话,就会更为复杂,两个参数的时候就已经是三维图像了: 
高度即为代价函数的值,可以看到它仍然有着最小值的,而到达更多的参数的时候就无法像这样可视化了,但是原理都是相似的。
因此,对于回归问题,我们就可以归结为得到代价函数的最小值: 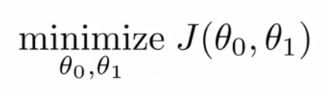
二.Multivariate Linear regression(多元线性回归)
现在起将开始介绍一种新的更为有效的线性回归形式。这种形式适用于多个变量或者多特征量的情况。
在之前学习过的线性回归中,都是只有一个单一的特征量--房屋面积 x,如图1-1所示,
图1-1
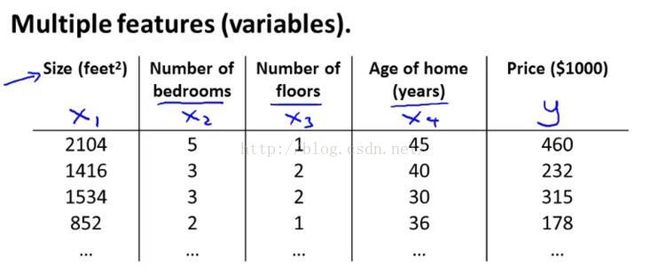
我们希望用房屋面积这个特征量来预测房子的价格。但是想象一下如果我们不仅有房屋面积作为预测房屋价格的特征量,我们还知道卧室的数量,楼层的数量以及房子的使用年限,如图1-2所示,
图1-2
这样就给了我们更多可以用来预测房屋价格的信息了。接着我们先简单介绍一下符号记法,一开始的时候就提到过我要用x1,x2,x3,x4来表示种情况下的四个特征量,然后仍然用 y来表示我们所想要预测的输出变量 。除此之外,我们来看看更多的表示方式,如图1-3
[第i个训练样本;第i个训练样本中第j个参数值]
图1-3
首先介绍的是特征数量n,这里用小写n来表示特征量的数目。因此在这个例子中,我们的n等于4(之前我们是用的“m”来表示样本的数量,现在开始我们用n来表示特征量的数目)。
接着介绍的是第i个训练样本的输入特征值x(i)(这里一定要看清是上标,不要搞混了)。举个具体的例子来说x(2)就是表示第二个训练样本的特征向量,如图1-4中用红色框圈起来的位置,
图1-4
红色框圈起来的这四个数字对应了我用来预测第二个房屋价格的四个特征量,因此在这种记法中,这个上标2就是训练集的一个索引,而不是x的2次方,这个2就对应着你所看到的表格中的第二行,即我的第二个训练样本,同时也是一个四维向量。事实上更普遍
地来说这是n维的向量。
最后介绍的是第i个训练样本的第j个特征量,用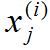 来表示。举个具体的例子来说:
来表示。举个具体的例子来说:
我们最初使用的假设函数只有一个唯一的特征量,如图1-5黑色字体,
图1-5
但现在我们有了多个特征量,我们就不能再使用这种简单的表示方式了。取而代之的我们将把线性回归的假设改成图1-5中蓝色字体那样。如果我们有n个特征量,那么我们要将所有的n个特征量相加,而不仅仅是四个特征量,如图1-6所示。
图1-6
接下来,要做的是简化这个等式的表示方式,为了表示方便我要将x0的(看清楚这里是下标)值设为1。具体而言,这意味着对于第i个样本,都有一个![]() 等于1。一开始的时候有n个特征量,由于另外定义了额外的第0个特征向量,并且它的取值总是1,所以我现在的特征向量x是一个从0开始标记的n+1维的向量。同时,我也把我的参数θ也都看做一个n+1维的向量。如图1-7所示
等于1。一开始的时候有n个特征量,由于另外定义了额外的第0个特征向量,并且它的取值总是1,所以我现在的特征向量x是一个从0开始标记的n+1维的向量。同时,我也把我的参数θ也都看做一个n+1维的向量。如图1-7所示
图1-7
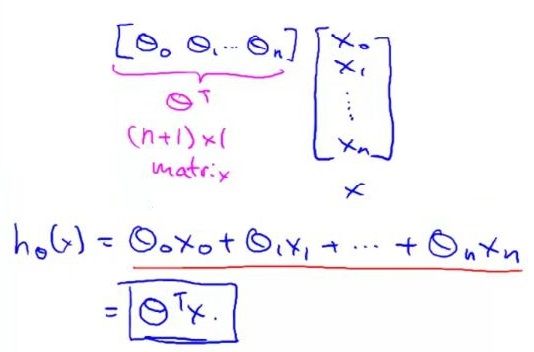
正是向量的引入,这里我们的假设函数可以换一种更加高效的方式来写,如图1-8,
图1-8
这里我把假设函数等式写成 θ转置乘以X,这其实就是向量内积。这就为我们提供了一个表示假设函数更加便利的形式,即用参数向量θ以及特征向量X的内积。这样的表示习惯就让我们可以以这种紧凑的形式写出假设。
以上就是多特征量情况下的假设形式,另一个名字就是多元线性回归。
二.Gradient Descent for Multiple Variables(多元线性回归的梯度下降)
在之前我们谈到的线性回归的假设形式,是一种有多特征或者是多变量的形式。在这部分我们将会谈到如何找到满足这一假设的参数θ,尤其是如何使用梯度下降法来解决多特征的线性回归问题。
现假设有多元线性回归,并约定x0=1,该模型的参数是从θ0到θn,如图2-1所示,
图2-1
这里不要认为这是n+1个单独的参数,我们要把这n+1个θ参数想象成一个n+1维的向量θ。
我们一开始的代价函数如图2-2黑色字体所示,
图2-2
但同样地我们不要把函数J想成是一个关于n+1个自变量的函数,而是看成带有一个n+1维向量的函数。
-----------------------------------------------------------------------------
关于图2-2的这个公式要深入理解下,见图2-3的练习
图2-3
一开始选了2和4,提交后得知应该选择1和2。分析如下:
选项1.其实这里的x(i)拆开后是![]() ,然后和θ的转置相乘,结果与
,然后和θ的转置相乘,结果与![]() 是一样的。
是一样的。
选项3.从1开始错误,我们规定了要从0开始。
选项4.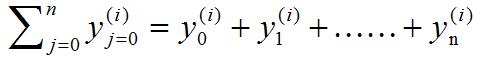 ,因为我们的y不像x有x0,x1,x2等等,y是没有下标只有上标的,所以选项4错误。
,因为我们的y不像x有x0,x1,x2等等,y是没有下标只有上标的,所以选项4错误。
-----------------------------------------------------------------------------
-----------------------------------------------------------------------------------------------------------------------------
https://www.cnblogs.com/ooon/p/4947688.html
1 问题的引出
对于上篇中讲到的线性回归,先化一个为一个特征θ1,θ0为偏置项,最后列出的误差函数如下图所示:
手动求解
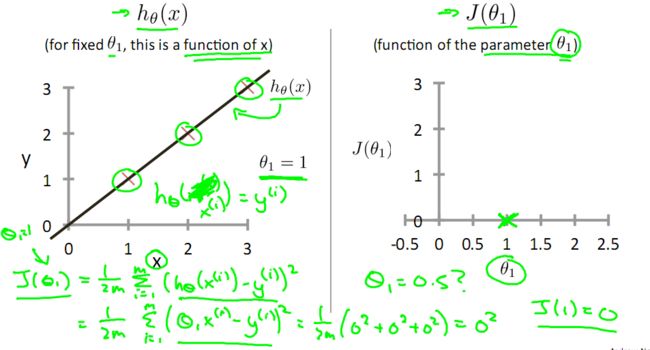
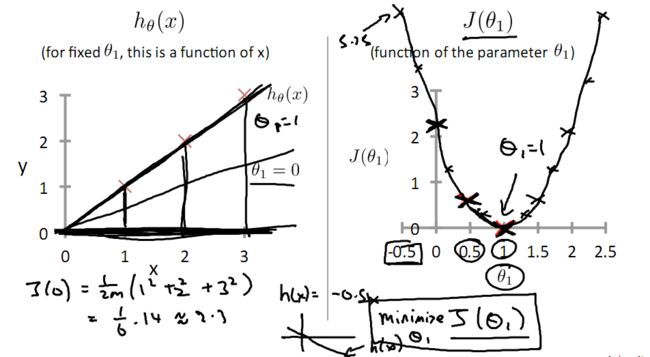
目标是优化J(θ1),得到其最小化,下图中的×为y(i),下面给出TrainSet,{(1,1),(2,2),(3,3)}通过手动寻找来找到最优解,由图可见当θ1取1时,![]() 与y(i)完全重合,J(θ1) = 0
与y(i)完全重合,J(θ1) = 0
下面是θ1的取值与对应的J(θ1)变化情况
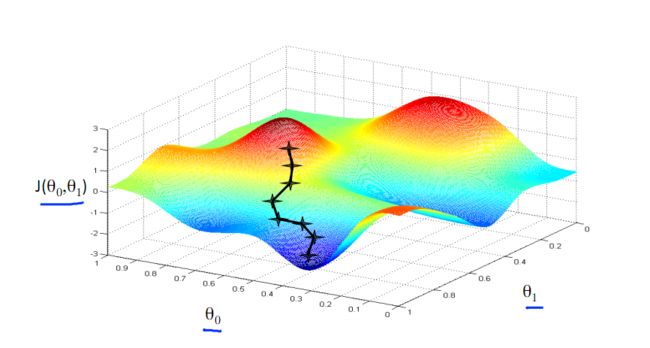
由此可见,最优解即为0,现在来看通过梯度下降法来自动找到最优解,对于上述待优化问题,下图给出其三维图像,可见要找到最优解,就要不断向下探索,使得J(θ)最小即可。
2 梯度下降的几何形式
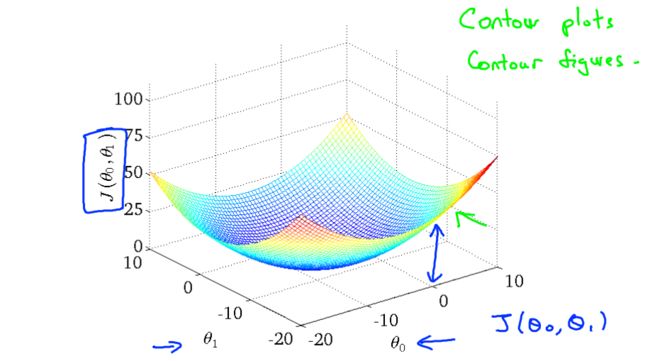
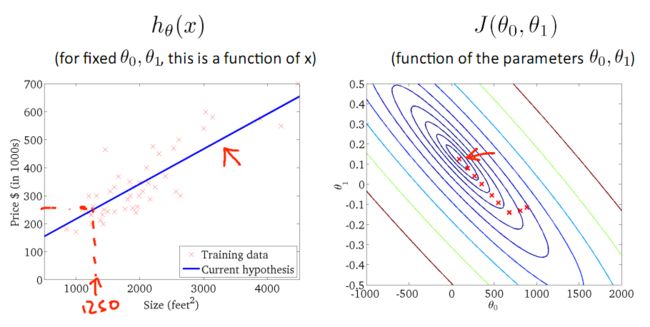
下图为梯度下降的目的,找到J(θ)的最小值。
其实,J(θ)的真正图形是类似下面这样的,因为其是一个凸函数,只有一个全局最优解,所以不必担心像上图一样找到局部最优解
直到了要找到图形中的最小值之后,下面介绍自动求解最小值的办法,这就是梯度下降法
对参数向量θ中的每个分量θj,迭代减去速率因子a* (dJ(θ)/dθj)即可,后边一项为J(θ)关于θj的偏导数
3 梯度下降的原理
导数的概念
由公式可见,对点x0的导数反映了函数在点x0处的瞬时变化速率,或者叫在点x0处的斜度。推广到多维函数中,就有了梯度的概念,梯度是一个向量组合,反映了多维图形中变化速率最快的方向。
下图展示了对单个特征θ1的直观图形,起始时导数为正,θ1减小后并以新的θ1为基点重新求导,一直迭代就会找到最小的θ1,若导数为负时,θ1的就会不断增到,直到找到使损失函数最小的值。
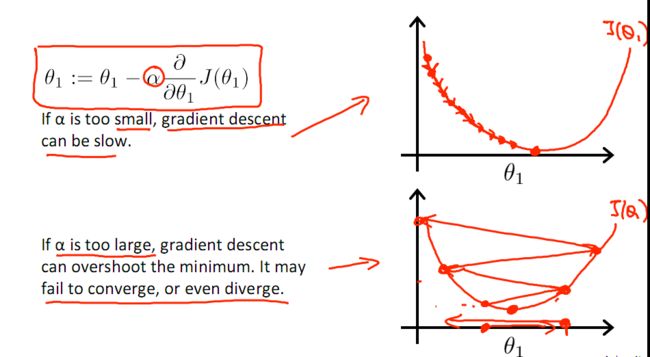
有一点需要注意的是步长a的大小,如果a太小,则会迭代很多次才找到最优解,若a太大,可能跳过最优,从而找不到最优解。
另外,在不断迭代的过程中,梯度值会不断变小,所以θ1的变化速度也会越来越慢,所以不需要使速率a的值越来越小
下图就是寻找过程
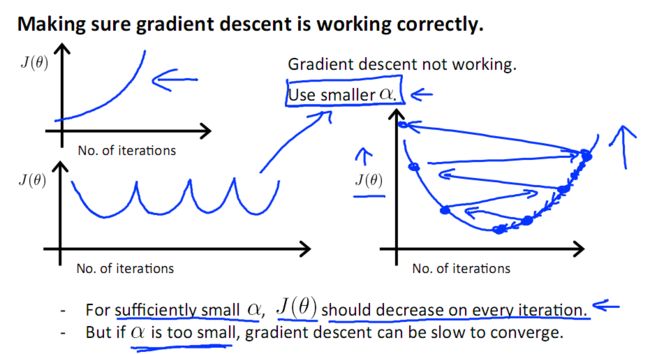
当梯度下降到一定数值后,每次迭代的变化很小,这时可以设定一个阈值,只要变化小鱼该阈值,就停止迭代,而得到的结果也近似于最优解。
若损失函数的值不断变大,则有可能是步长速率a太大,导致算法不收敛,这时可适当调整a值
为了选择参数a,就需要不断测试,因为a太大太小都不太好。
如果想跳过的a与算法复杂的迭代,可以选择 Normal Equation。
4 随机梯度下降
对于样本数量额非常之多的情况,Batch Gradient Descent算法会非常耗时,因为每次迭代都要便利所有样本,可选用Stochastic Gradient Descent 算法,需要注意外层循环Loop,因为只遍历一次样本,不见得会收敛。
随机梯度算法就可以用作在线学习了,但是注意随机梯度的结果并非完全收敛,而是在收敛结果处波动的,可能由非线性可分的样本引起来的:
可以有如下解决办法:(来自MLIA)
1. 动态更改学习速率a的大小,可以增大或者减小
2. 随机选样本进行学习
-----------------------------------------------------------------------------------------------------------------------------
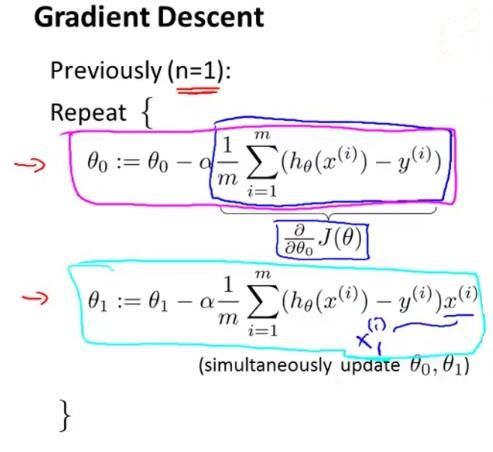
讲完代价函数,讲梯度下降,如图2-4所示,
图2-4
同理这里把函数J想成是带有一个n+1维向量的函数。当我们实现梯度下降法后,我们可以仔细观察一下它的偏导数项,图2-5是我们当特征个数n=1时梯度下降的情况。我们有两条针对参数θ0和θ1不同的更新规则,
图2-5
图2-5的两个式子不同点在于对参数θ1我们有另一个更新规则,即在最后多了一项
X(i)。(http://blog.csdn.net/m399498400/article/details/52528722图1-2中讲解了这一项的推导过程)。
----------------------------推导过程------------------结合复合函数的求导(对什么参数求导,其他的参数就当做常数)--------
-----------------------------------------------------------------------------------------------------------------------------
以上是特征数量只有1个的情况下的梯度下降法的实现。当特征数量大于等于1个的时候,我们的梯度下降更新规则,变成了如图2-6的形式。
图2-6
其实图2-5和图2-6这两种新旧算法实际上是一回事儿。考虑这样一个情况,假设我们有3个特征数量,我们就会有对θ1、θ2、θ3的三条更新规则。如图2-7所示,
图2-7
仔细观察θ0的更新规则,就会发现这跟之前图2-5中n=1的情况是相同的。它们之所以是等价的是因为在我们的标记约定里有![]() =1。
=1。
如果再仔细观察θ1的更新规则,会发现这里的这一项是和图2-5对参数θ1的更新项是等价的。在图2-7中我们只是用了新的符号![]() 来表示我们的第一个特征。其实当n=1的时候,
来表示我们的第一个特征。其实当n=1的时候,![]() 和
和![]() 是一样的。因为图2-7的新算法应用更普遍,更广泛,所以以后不管是单特征变量还是多特征变量我们都用图2-7的算法来做梯度下降。
是一样的。因为图2-7的新算法应用更普遍,更广泛,所以以后不管是单特征变量还是多特征变量我们都用图2-7的算法来做梯度下降。