优达学城-深度学习笔记(一)
优达学城-深度学习笔记(一)
标签: 机器学习
- 优达学城-深度学习笔记一
-
- 一 神经网络简介
- 最大似然概率
- 交叉熵Cross entropy
- 1交叉熵代码实现
- 2多类别交叉熵
- 对数几率回归的误差函数cost function
- 梯度下降代码
- 神经网络
- 2 反向传播
- 二梯度下降的神经网络
- 梯度下降代码实现
- 反向传播示例
- 反向传播代码实现
- 三训练神经网络
- 正则化
- dropout
- Keras 中的其他激活函数
- Keras 中的随机梯度下降
- 随机重新开始
- 动量解决局部最优解
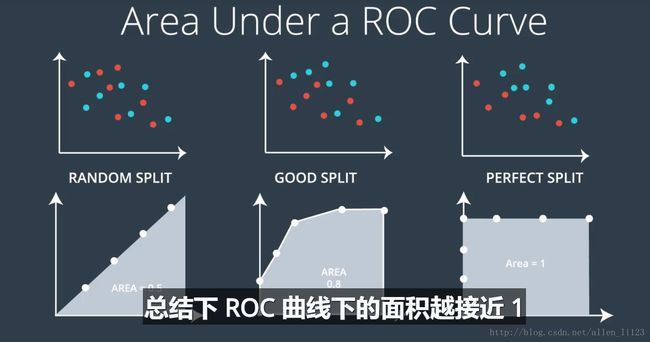
- ROC 曲线
- 一 神经网络简介
-
一. 神经网络简介
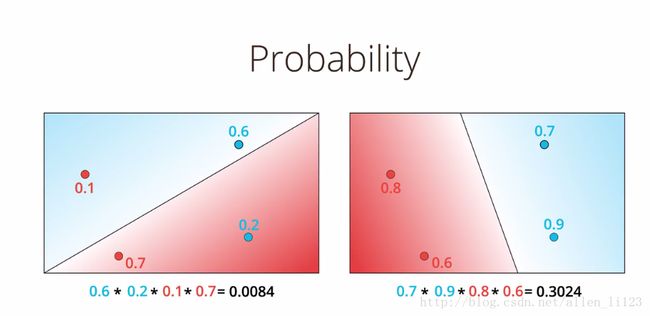
1.最大似然概率
将可能分类正确的概率相乘,将全部分类正确的概率做比较,最大的即为最优的
2.交叉熵(Cross entropy)
由于很多数相乘值会非常小,于是采用-ln进行相加,更小的交叉熵更优

2.1交叉熵代码实现
def cross_entropy(Y, P):
Y=np.float_(Y)
P=np.float_(P)
ans=-np.sum(Y*np.log(P)+(1-Y)*np.log(1-P))
return ans2.2多类别交叉熵
3.对数几率回归的误差函数(cost function)
goal:最小化误差函数
4.梯度下降代码
随机初始化一个权重
w1...,wn,b对于每一个分类点( x1,...xn )
2.1 For i=1…n
2.1.1. 更新 wi=wi−α(y−y′)xi
2.1.2 更新 b=b−α(y−y′)- 重复步骤2直到误差最小
# Implement the following functions
# Activation (sigmoid) function
def sigmoid(x):
return 1/(1+np.exp(-x))
# Output (prediction) formula
def output_formula(features, weights, bias):
return sigmoid(np.dot(features, weights) + bias)
# Error (log-loss) formula
def error_formula(y, output):
return - y*np.log(output) - (1 - y) * np.log(1-output)
# Gradient descent step
def update_weights(x, y, weights, bias, learnrate):
output = output_formula(x, weights, bias)
d_error = -(y - output)
weights -= learnrate * d_error * x
bias -= learnrate * d_error
return weights, bias5.神经网络
当存在非线性数据时,例如需要用曲线进行划分,则用神经网络
5.1 前向传播
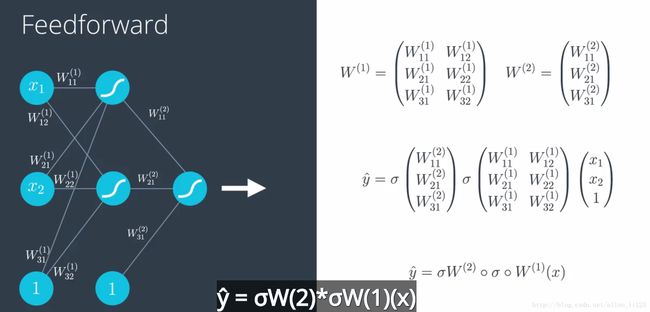
5.2 反向传播
反向传播包括:
2.1 进行前向反馈运算。
2.2 将模型的输出与期望的输出进行比较。
2.3 计算误差。
2.4 向后运行前向反馈运算(反向传播),将误差分散到每个权重上。
2.5 更新权重,并获得更好的模型。
2.6 继续此流程,直到获得很好的模型。
二.梯度下降的神经网络
1.梯度下降代码实现
# Defining the sigmoid function for activations
# 定义 sigmoid 激活函数
def sigmoid(x):
return 1/(1+np.exp(-x))
# Derivative of the sigmoid function
# 激活函数的导数
def sigmoid_prime(x):
return sigmoid(x) * (1 - sigmoid(x))
# Input data
# 输入数据
x = np.array([0.1, 0.3])
# Target
# 目标
y = 0.2
# Input to output weights
# 输入到输出的权重
weights = np.array([-0.8, 0.5])
# The learning rate, eta in the weight step equation
# 权重更新的学习率
learnrate = 0.5
# the linear combination performed by the node (h in f(h) and f'(h))
# 输入和权重的线性组合
h = x[0]*weights[0] + x[1]*weights[1]
# or h = np.dot(x, weights)
# The neural network output (y-hat)
# 神经网络输出
nn_output = sigmoid(h)
# output error (y - y-hat)
# 输出误差
error = y - nn_output
# output gradient (f'(h))
# 输出梯度
output_grad = sigmoid_prime(h)
# error term (lowercase delta)
error_term = error * output_grad
# Gradient descent step
# 梯度下降一步
del_w = [ learnrate * error_term * x[0],
learnrate * error_term * x[1]]
# or del_w = learnrate * error_term * x2.反向传播示例
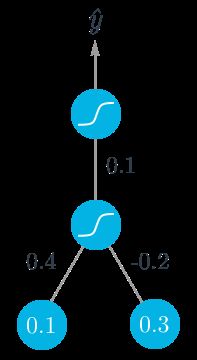
先使用正向传播计算输入层到隐藏层节点:
h=∑iwixi=0.1∗0.4−0.2∗0.3=−0.02计算隐藏节点的输出
a=f(h)=sigmoid(−0.02)=0.495将其作为输出节点的输入,该神经网络的输出可表示为
y^=f(W∗a)=sigmoid(0.1∗0.495)=0.512根据神经网络的输出,用反向传播更新各层的权重,sigmoid函数的倒数为 f′(W∗a)=f(W∗a)(1−f(W∗a)) ,输出节点的误差项可表示为
δo=(y−y^)f′(W∗a)=(1−0.512)∗0.512∗(1−0.512)=0.122计算隐藏节点的误差项
δhj=∑kWjkδokf′(hj)
因为只有一个隐藏节点
δh=Wδof′(h)=0.1∗0.122∗0.495∗(1−0.495)=0.003计算梯度下降步长了。隐藏层-输出层权重更新步长是学习速率乘以输出节点误差再乘以隐藏节点激活值。
ΔW=αδoa=0.5∗0.122∗0.495=0.0302输入-隐藏层权重 wi 是学习速率乘以隐藏节点误差再乘以输入值。
Δwi=αδhxi=(0.5∗0.003∗0.1,0.5∗0.003∗0.3)=(0.00015,0.00045)
3.反向传播代码实现
import numpy as np
from data_prep import features, targets, features_test, targets_test
np.random.seed(21)
def sigmoid(x):
"""
Calculate sigmoid
"""
return 1 / (1 + np.exp(-x))
# Hyperparameters
n_hidden = 2 # number of hidden units
epochs = 900
learnrate = 0.005
n_records, n_features = features.shape
last_loss = None
# Initialize weights
weights_input_hidden = np.random.normal(scale=1 / n_features ** .5,
size=(n_features, n_hidden))
weights_hidden_output = np.random.normal(scale=1 / n_features ** .5,
size=n_hidden)
for e in range(epochs):
del_w_input_hidden = np.zeros(weights_input_hidden.shape)
del_w_hidden_output = np.zeros(weights_hidden_output.shape)
for x, y in zip(features.values, targets):
## Forward pass ##
# TODO: Calculate the output
hidden_input = np.dot(x, weights_input_hidden)
hidden_output = sigmoid(hidden_input)
output = sigmoid(np.dot(hidden_output,
weights_hidden_output))
## Backward pass ##
# TODO: Calculate the network's prediction error
error = y - output
# TODO: Calculate error term for the output unit
output_error_term = error * output * (1 - output)
## propagate errors to hidden layer
# TODO: Calculate the hidden layer's contribution to the error
hidden_error = np.dot(output_error_term, weights_hidden_output)
# TODO: Calculate the error term for the hidden layer
hidden_error_term = hidden_error * hidden_output * (1 - hidden_output)
# TODO: Update the change in weights
del_w_hidden_output += output_error_term * hidden_output
del_w_input_hidden += hidden_error_term * x[:, None]
# TODO: Update weights
weights_input_hidden += learnrate * del_w_input_hidden / n_records
weights_hidden_output += learnrate * del_w_hidden_output / n_records
# Printing out the mean square error on the training set
if e % (epochs / 10) == 0:
hidden_output = sigmoid(np.dot(x, weights_input_hidden))
out = sigmoid(np.dot(hidden_output,
weights_hidden_output))
loss = np.mean((out - targets) ** 2)
if last_loss and last_loss < loss:
print("Train loss: ", loss, " WARNING - Loss Increasing")
else:
print("Train loss: ", loss)
last_loss = loss
# Calculate accuracy on test data
hidden = sigmoid(np.dot(features_test, weights_input_hidden))
out = sigmoid(np.dot(hidden, weights_hidden_output))
predictions = out > 0.5
accuracy = np.mean(predictions == targets_test)
print("Prediction accuracy: {:.3f}".format(accuracy))
三.训练神经网络
1.正则化
1.倾向于获得稀疏向量
2.倾向于获得低权重向量
2.dropout
在训练神经网络时为了确保每一个节点都能被很好的训练,会随机关闭一些节点,关闭概率可以设置为20%
3.Keras 中的其他激活函数
更改激活函数很简单。到目前为止,我们一直在使用 s 型函数(如果有多个类别,则使用 softmax,例如我们对输出进行一位热码编码时),并按以下方式添加到层级中:
model.add(Activation('sigmoid'))
或
model.add(Activation('softmax'))
如果我们要使用 relu或 tanh,则直接将层级名称指定为 relu 或 tanh:
model.add(Activation('relu'))
model.add(Activation('tanh'))
4.Keras 中的随机梯度下降
在 Keras 中很容易实现随机梯度下降。我们只需按以下命令在训练流程中指定批次大小:
model.fit(X_train, y_train, epochs=1000, batch_size=100, verbose=0)
这里,我们将数据分成 100 批。
5.随机重新开始
为了防止进入局部最优解,多次随机重新找起始点以解决局部最优问题
6.动量解决局部最优解
同样局部最优的问题,可以用动量的方法来改变学习速率
这样就可能会越过局部最优解