深入理解L0，L1和L2正则化

正则化技术是机器学习中常用的技术，一般是用来解决过拟合问题的。为什么范数可以作为机器学习的正则化项？为什么L1正则化可以用来进行特征选择的工作？为什么正则化可以解决过拟合问题？本篇博客从机器学习中为什么需要范数讲起，引出$L_0$，$L_1$ 和 $L_2$的定义，然后回答上述的问题。

一、损失函数与目标函数

机器学习的目标，实际上就是找到一个足够好的函数$F^{\ast }$用以预测真实规律。因此，首先我们要定义什么叫做「好」。

对于样本$(x,y)$ 来说，在机器学习模型 $F$ 的作用下，有预测值 $\hat{y}=F(x)$。我们可以定义损失函数 $l(y,\hat{y})$，来描述预测值 $\hat{y}$与 真值$y$ 之间的差距:
$$l(y,\hat{y})=l(y,F(x))$$

一般来说，损失函数$l$是一个有下确界的函数。当预测值$\hat{y}$与上帝真相$y$相差不多时，则损失函数的值能接近这个下确界；反之，当预测值 $\hat{y}$与上帝真相 $y$ 差距甚远时，损失函数的值会显著地高于下确界。

因此，在整个训练集上，我们可以把机器学习任务转化为一个最优化问题。我们的目标是在泛函空间内，找到能使得全局损失 $L(F)$ 最小的模型$F$，作为最终模型$F^{\ast }$:
$$F^{\ast }={\text{arg min}}_F{E}_{y,x}\left[l\right(y,F(x)\left)\right]={\text{arg min}}_{F}L(F)$$

这样的最优化问题解决了机器学习的大半任务，但是它只考虑了对数据的拟合，而忽视了模型本身的复杂度。因此，它留下了一个显而易见的问题：如何防止模型本身的复杂度过高，导致过拟合？为此，我们需要引入正则项（regularizer)$\gamma \Omega (F),\gamma >0$，用来描述模型本身的复杂度。于是我们的最优化目标变为
$$F^{\ast }={\text{arg min}}_F\text{Obj}(F)={\text{arg min}}_{F}L(F)+\gamma \Omega (F)$$

二、范数与正则项

2.1 定义

所谓范数，就是某种抽象的长度。范数满足通常意义上长度的三个基本性质：

• 非负性：$\Vert x\Vert ⩾0$；
• 齐次性：$\Vert c\cdot x\Vert =|c|\cdot \Vert x\Vert$；
• 三角不等式：$\Vert x+y\Vert ⩽\Vert x\Vert +\Vert y\Vert$。

在这里，我们需要关注的最主要是范数的「非负性」。我们刚才讲，损失函数通常是一个有下确界的函数。而这个性质保证了我们可以对损失函数做最优化求解。如果我们要保证目标函数依然可以做最优化求解，那么我们就必须让正则项也有一个下界。非负性无疑提供了这样的下界，而且它是一个下确界——由齐次性保证（当 $c=0$ 时）。

因此，我们说，范数的性质使得它天然地适合作为机器学习的正则项。而范数需要的向量，则是机器学习的学习目标——参数向量。

机器学习中有几个常用的范数，分别是

• $L_0$-范数：$\Vert x{\Vert }_0=\#(i)$，$i$不等于0；
• $L_1$-范数：$\Vert x{\Vert }_1={\sum }_{i=1}^d|x_i|$；
• $L_2$-范数：$\Vert x{\Vert }_2=({\sum }_{i=1}^d{x}_i^2{)}^{1/2}$；
• $L_p$-范数：$\Vert x{\Vert }_p=({\sum }_{i=1}^d{x}_i^p{)}^{1/p}$；
• $L_{\infty }$-范数：$\Vert x{\Vert }_{\infty }={\lim }_{p\to +\infty }({\sum }_{i=1}^d{x}_i^p{)}^{1/p}$。

在机器学习中，如果使用了$\Vert w{\Vert }_p$ 作为正则项；则我们说，该机器学习任务引入了$L_p$-正则项。

我们通常引入的正则项是$L_1$和$L_2$。为什么不引入$L_0$呢？从定义我们就可以看出来，$L_0$范数非连续，不可求导。

2.2 L1和L2 范数的对比

2.2.1 鲁棒性： L1＞L2

鲁棒性定义为对数据集中异常值的容忍力。

$L_1$范数比$L_2$范数更鲁棒，原因相当明显：从定义中可以看到，$L_2$范数取平方值，因此它以指数方式增加异常值的影响；$L_1$范数只取绝对值，因此它会线性地考虑它们。

2.2.2 计算困难：L1＞L2

从定义中可以看到，$L_2$范数是连续的，因此，它有一个闭式解。但$L_1$范数涉及到绝对值，它是一个不可微的分段函数。由于这个原因，$L_1$在计算上代价更高，因为我们无法用矩阵数学来解决它。

2.2.3 解的数量：L1多个，L2一个

从下图中我们就可以清晰的看出来，求解2个点的距离时，$L_2$只有1个绿色的解，而$L_1$却有多个解。这也是由于定义造成的。

2.2.4 稀疏性：L1＞L2

我们都知道，因为$L_1$天然的输出稀疏性，把不重要的特征都置为 0，所以它也是一个天然的特征选择器。那么为什么$L_1$可以产生更稀疏的解呢。这里用个直观的例子来讲解。

我们已经知道$L_1$和$L_2$的定义如下：

• $L_1$-范数：$\Vert w{\Vert }_1={\sum }_{i=1}^d|w_i|$；
• $L_2$-范数：$\Vert w{\Vert }_2=({\sum }_{i=1}^d{w}_i^2{)}^{1/2}$；

在数学中，如何求一个方程的最小值，三部曲是：“求导，置零，解方程” 。当然，对于我们的机器学习的目标函数时，第一步也是求导。于是分别先对 $L_1$和$L_2$来进行求导，可得：
$$\frac{d{L}_1(w)}{dw}=sign(w)，\frac{d{L}_2(w)}{dw}=w$$

之后将 $L_1$和$L_2$ 和它们的导数画在图上

于是会发现，在梯度更新时，不管 $L_1$的大小是多少（只要不是0）梯度都是1或者-1，所以每次更新时，它都是稳步向0前进。

而看$L_2$的话，就会发现它的梯度会越靠近0，就变得越小。

也就是说加了 $L_1$正则的话基本上经过一定步数后很可能变为0，而 $L_2$几乎不可能，因为在值小的时候其梯度也会变小。于是也就造成了 L1 输出稀疏的特性。

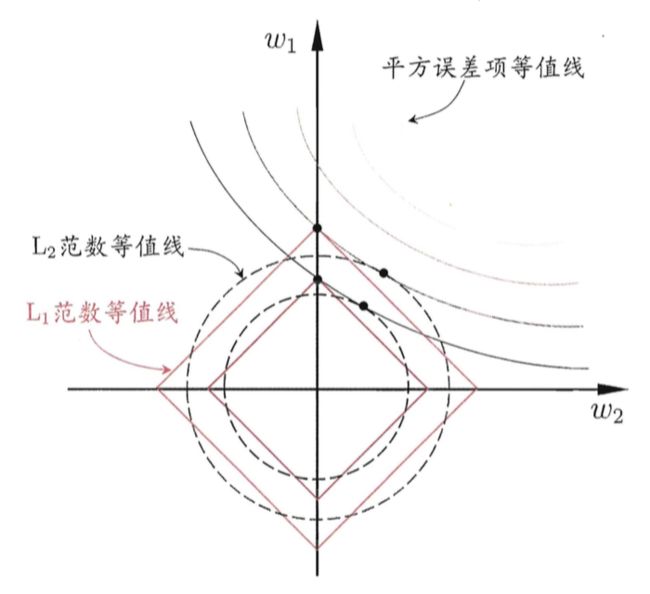
关于$L_1$范数为什么会稀疏，周志华老师的著作《机器学习》里也有一张插图，尝试解释这个问题。

为了简便起见，我们只考虑模型有两个参数 $w_1$ 与 $w_2$ 的情形。

在图中，我们有三组「等值线」。位于同一条等值线上的$w_1$ 与 $w_2$，具有相同的值（平方误差、$L_1$范数或$L_2$范数）。并且，对于三组等值线来说，当 $(w_1,w_2)$ 沿着等值线法线方向，像外扩张，则对应的值增大；反之，若沿着法线方向向内收缩，则对应的值减小。

因此，对于目标函数 $Obj(F)$ 来说，实际上是要在正则项的等值线与损失函数的等值线中寻找一个交点，使得二者的和最小。

对于$L_1$正则项来说，因为 $L_1$正则项的等值线是一组菱形，这些交点容易落在坐标轴上。因此，另一个参数的值在这个交点上就是零，从而实现了稀疏化。

对于 $L_2$正则项来说，因为 $L_2$正则项的等值线是一组圆形。所以，这些交点可能落在整个平面的任意位置。所以它不能实现「稀疏化」。但是，另一方面，由于 $(w_1,w_2)$ 落在圆上，所以它们的值会比较接近。这就是为什么 $L_2$正则项可以使得参数在零附近稠密而平滑。

三、为什么正则化可以防止过拟合

正则化能帮助减少过拟合。这是令人高兴的事，然而不幸的是，我们没有明显的证据证明为什么正则化可以起到这个效果。

目前一个通俗一点的解释是：

拟合过程中通常都倾向于让权值尽可能小，最后构造一个所有参数都比较小的模型。因为一般认为参数值小的模型比较简单，能适应不同的数据集，也在一定程度上避免了过拟合现象。可以设想一下对于一个线性回归方程，若参数很大，那么只要数据偏移一点点，就会对结果造成很大的影响；但如果参数足够小，数据偏移得多一点也不会对结果造成什么影响，专业一点的说法是鲁棒性强。

以线性回归中的梯度下降法为例，正好重新复习一遍。

假设有$m$个样本，假设函数（参数由$\theta$表示）如下：
$$h_{\theta }(x)={\theta }_0+{\theta }_{1}x+{\theta }_2{x}^2\dots$$

我们的目标函数为：
$$J(\theta )=\frac{1}{2m}\sum _{i=1}^m(h_{\theta }(x^i)-y^i{)}^2$$

在梯度下降算法中，需要先对参数求导，得到梯度。梯度本身是上升最快的方向，为了让损失尽可能小，沿梯度的负方向更新参数即可。

对于某一个参数：
$${\theta }_j={\theta }_j-\alpha \frac{\partial J(\theta )}{\partial {\theta }_j}$$

而上式中
$$\frac{\partial J(\theta )}{\partial {\theta }_i}=\frac{1}{2m}\sum _{i=1}^m\frac{\partial (h_{\theta }(x^i)-y^i{)}^2}{\partial {\theta }_j}=\frac{2}{2m}\sum _{i=1}^m(h_{\theta }(x^i)-y^i)\frac{\partial h_{\theta }(x^i)}{\partial {\theta }_j}$$

继续推导：
$$\frac{\partial h_{\theta }(x^i)}{\partial {\theta }_j}=\frac{\partial ({\theta }_0{x}_0^i+{\theta }_1{x}_1^i+\cdots +{\theta }_j{x}_j^i+\cdots )}{\partial {\theta }_j}=\frac{\partial ({\theta }_j{x}_j^i)}{\partial {\theta }_j}=x_j^i$$

代入进去，有：
$${\theta }_j={\theta }_j-\alpha \frac{1}{m}\sum _{i=1}^m(h_{\theta }(x^i)-y^i)x_j^i\text{\hspace{1em}(1)}$$

（1）式是没有添加$L_2$正则化项的迭代公式，如果在原始代价函数之后添加$L_2$正则化，则迭代公式会变成下面的样子：
$${\theta }_j={\theta }_j(1-\alpha \frac{\lambda }{m})-\alpha \frac{1}{m}\sum _{i=1}^m(h_{\theta }(x^i)-y^i)x_j^i\text{\hspace{1em}(2)}$$

其中$\lambda$就是正则化参数。从上式可以看到，与未添加$L_2$正则化的迭代公式相比，每一次迭代，${\theta }_j$都要先乘以一个小于1的因子，从而使得${\theta }_j$不断减小，因此总得来看，与$L_2$不加入正则化相比，${\theta }_j$是减小的力度更大。

当然，我们在2.2.4节中已经可以看到，$L_1$正则在每次优化迭代时，参数$w$也总是在减少。因为对于正的参数来说，$L_1$使得它减小，对于负的参数来说，$L_1$使得它增大，总之参数的绝对值在减小。

因此，无论是$L_1$正则还是$L_2$正则，都符合我们期望的模型：即所有的参数都比较小。因此，正则可以防止过拟合现象。

参考文献：

【1】谈谈 L1 与 L2-正则项
【2】Why L1 norm for sparse models
【3】l1正则与l2正则的特点是什么，各有什么优势？
【4】机器学习中正则化项L1和L2的直观理解
【5】为什么正则化能够降低过拟合