深度学习（九）——花式卷积

花式卷积

在DL中，卷积实际上是一大类计算的总称。除了原始的卷积、反卷积（Deconvolution）之外，还有各种各样的花式卷积。

卷积在CNN和数学领域中的概念差异

首先需要明确一点，CNN中的卷积和反卷积，实际上和数学意义上的卷积、反卷积是有差异的。

数学上的卷积主要用于傅立叶变换，在计算中有个时域上的反向操作，并不是简单的向量内积运算。在信号处理领域，卷积主要用作信号的采样。

数学上的反卷积主要作为卷积的逆运算，相当于信号的重建，或者解微分方程。因此，它的难度远远大于卷积运算，常见的有Wiener deconvolution、Richardson–Lucy deconvolution等。

CNN的反卷积就简单多了，它只是误差的反向算法而已。因此，也有人用back convolution, transpose convolution这样更精确的说法，来描述CNN的误差反向算法。

Dilated convolution

上图是Dilated convolution的操作。又叫做多孔卷积(atrous convolution)。

上图是transpose convolution的操作。它和Dilated convolution的差别在于，前者是图像上有洞，而后者是kernel上有洞。

和池化相比，Dilated convolution实际上也是一种下采样，只不过采样的位置是固定的，因而能够更好的保持空间结构信息。

Dilated convolution在CNN方面的应用主要是Fisher Yu的贡献。

论文：

《Multi-Scale Context Aggregation by Dilated Convolutions》

《Dilated Residual Networks》

代码：

https://github.com/fyu/dilation

https://github.com/fyu/drn

Fisher Yu，密歇根大学本硕+普林斯顿大学博士。
个人主页：
http://www.yf.io/

参考：

https://zhuanlan.zhihu.com/p/28822428

Paper笔记：Dilated Residual Networks

分组卷积

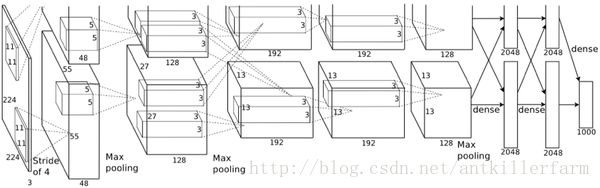
分组卷积最早在AlexNet中出现，由于当时的硬件资源有限，训练AlexNet时卷积操作不能全部放在同一个GPU处理，因此作者把feature maps分给2个GPU分别进行处理，最后把2个GPU的结果进行融合。

在AlexNet的Group Convolution当中，特征的通道被平均分到不同组里面，最后再通过两个全连接层来融合特征，这样一来，就只能在最后时刻才融合不同组之间的特征，对模型的泛化性是相当不利的。

为了解决这个问题，ShuffleNet在每一次层叠这种Group conv层前，都进行一次channel shuffle，shuffle过的通道被分配到不同组当中。进行完一次group conv之后，再一次channel shuffle，然后分到下一层组卷积当中，以此循环。

论文：

《ShuffleNet: An Extremely Efficient Convolutional Neural Network for Mobile Devices》

无论是在Inception、DenseNet或者ShuffleNet里面，我们对所有通道产生的特征都是不分权重直接结合的，那为什么要认为所有通道的特征对模型的作用就是相等的呢？这是一个好问题，于是，ImageNet2017冠军SEnet就出来了。

论文：

《Squeeze-and-Excitation Networks》

Separable convolution

前面介绍的都是正方形的卷积核，实际上长条形的卷积核也是很常用的。比如可分离卷积。

我们知道卷积的计算量和卷积核的面积成正比。对于k x k的卷积核K来说，计算复杂度就是 O(k2) 。

如果我们能找到1 x k的卷积核H和k x 1的卷积核V，且 K=V∗H ，则称K是可分离的卷积核。

根据卷积运算满足结合律，可得：

f∗K=f∗(V∗H)=f∗V∗H

这样就将一个k x k的卷积运算，转换成1 x k + k x 1的卷积运算，从而大大节省了参数和计算量。

显然，不是所有的卷积核都满足可分离条件。但是不要紧，NN有自动学习并逼近函数的能力。经过训练之后： K≈V∗H

可变形卷积核

MSRA于2017年提出了可变形卷积核的概念。

论文：

《Deformable Convolutional Networks》

1 x 1卷积

1、升维或降维。

如果卷积的输出输入都只是一个平面，那么1x1卷积核并没有什么意义，它是完全不考虑像素与周边其他像素关系。 但卷积的输出输入是长方体，所以1 x 1卷积实际上是对每个像素点，在不同的channels上进行线性组合（信息整合），且保留了图片的原有平面结构，调控depth，从而完成升维或降维的功能。

2、加入非线性。卷积层之后经过激励层，1 x 1的卷积在前一层的学习表示上添加了非线性激励（non-linear activation），提升网络的表达能力；

3.促进不同通道之间的信息交换。

参考：

https://www.zhihu.com/question/56024942

卷积神经网络中用1x1卷积有什么作用或者好处呢？

depthwise separable convolution

在传统的卷积网络中，卷积层会同时寻找跨空间和跨深度的相关性。

然而Xception指出：跨通道的相关性和空间相关性是完全可分离的，最好不要联合映射它们。

Xception是Francois Chollet于2016年提出的。

上图是Xception中的卷积运算depthwise separable convolution的示意图。