《机器学习实战》之决策树ID3、C4.5、CART算法【二】
环境: win10 64位+Python3.6.0
说明:本系列文章笔记将结合《统计学习方法》一起来说明,因为这两本书刚好实现了理论与实践的完美结合,既没有理论的那种枯燥无味的不适感,也没有一昧追求动手(敲代码)的能力而忽略了理论原理性的东西!所以更能很好的把握算法的原理与实现过程吧。
资料: 本系列博客设计的书籍及其相关代码http://pan.baidu.com/s/1i5GbyRj 密码:orfe
优缺点:
- 优点:计算复杂度不高,输出结果易于理解,对中间值的缺失 不敏感,可以处理不相关特征数据。
- 缺点:可能会产生过度匹配问题。
适应的数据类型: 数值型和标称型。
第一部分:原理简介
《统计学习方法》书中很好的阐述了决策树的原理。决策树是一种基本的分类与回归方法,不过本文主要讨论的是用于分类的决策树。决策树学习通常包括3个步骤:特征选择,决策树的生成,决策树修剪。首先,对于决策树来说,它是通过某种策略来选择分类特征比较强的特征作为root根,然后通过递归的形式选择特征次一点的作为节点,分类结果则就是叶子的类别。决策树有以下几个版本:
Quinlan在1986年提出的ID3算法和1993年提出的C4.5算法,以及由Breiman等人在1984年提出的CART算法ID3与C4.5大致相同,要说不同ID3是通过信息增益来选择具有比较强的分类的特征,C4.5则是在ID3基础上提出改进通过信息增益比的大小来分类特征(由于只通过信息增益来划分训练数据集的特征,存在偏向于选择取值较多的特征的问题)。而CART(Classification and Regression Tree)分类与回归树是在给定输入随机变量X条件下输出随机变量Y的条件概率分布的学习方法。
在说明算法流程之前,咱得复习下,熵,条件熵,信息增益,信息增益比等。这些在《信息论》中有详细说明。
现贴出《统计学习方法》中的内容:

注:0log0=0
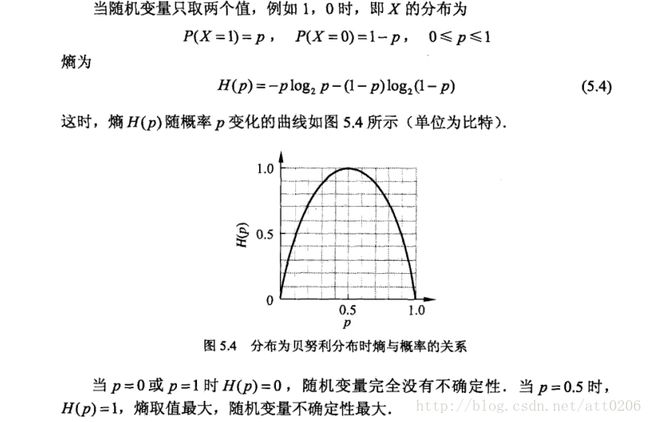
这上面主要详细的说明了熵,大家主要记住5.1那个式子就好了,在《机器学习实战》一书中称为经验熵,我觉得《统计学习方法》中的原理说得更加通俗易懂,所以以它为理论基础说明,以《机器学习实战》为实现。下面是条件熵的公式。

信息增益是经验熵减去条件熵得到的,具体如下所示:

信息增益比的定义如下所示:

这里给出相关字母的定义,这里当时没认真看就跳过了后来发现许多符号会很糊涂,所以建议这里认真看。如下图所示:

接下来给出信息增益的算法流程,主要就是要求得类别的经验熵,然后在求得在每个特征下的条件熵,信息增益就是经验熵-条件熵。这在之前的信息增益定义中已经很明确了,直接上流程:
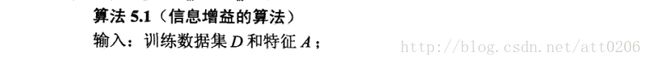

这里给出一个例子,便于大家理解,只要理解了原理后期通过Python编程的话还是很好实现的,所以先不急着编程,我们的目的是要知其所以然,如下表所示:
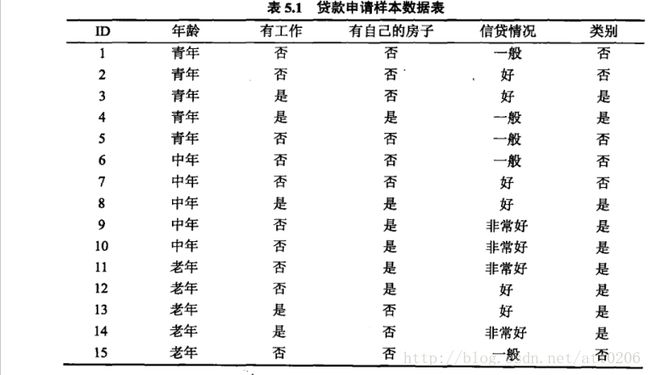
这是一份贷款的数据,以行为一个样本,以列为一个特征,可见不同样本的特征会影响最后的贷款与否,如果你是银行,肯定会想知道哪些特征会对最后的贷款结果影响比较大,哪些是对结果基本没什么影响或影响很小可以忽略的。所以这就面临了特征选择的问题,这就引出了利用信息增益来筛选特征的策略,这里给出计算信息增益的过程,便于理解。



通过计算信息增益可知有房子的特征信息增益最大,所以选择有房子作为root根节点,然后再通过递归的形式计算其他特征的信息增益从而得出一棵二叉树形式的决策树结构。
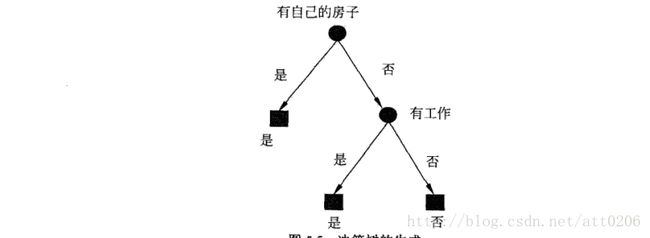
哈哈,通过以上的说明与贴图,大家是否明白了呢。多说一句,在得到有房子为根节点以后,接下来是通过计算除了有房子剩下来的数据集的信息增益,这个过程就形成了一个递归的形式。接下来将通过Python代=代码跟着实战书来实现这样的一个过程。上面这些都是引自《统计学习方法》里面的内容,我个人觉得这上面的讲解很清晰,所以可以通过这个来理解理论部分。资料见开头的链接,如果还需要其他关于机器学习方面资料的可以私信给我。同时也欢迎一起讨论交流!说完了基本原理,我们要开实战啦!
第二部分:ID3的Python实现
下面以海洋生物的表作为Python实现的数据集,如下所示:

首先我们可以根据表提供的数据来创建数据集,由上表可知,共有5个样本,两个特征分别为,特征中的“是”用1表示,“否”用0表示,类别中的“是”用yes表示,“否”用no表示,我们可以创建一个trees.py文件,创建一个如下的数据集:
def createDataSet():
dataSet = [[1, 1, 'yes'],
[1, 1, 'yes'],
[1, 0, 'no'],
[0, 1, 'no'],
[0, 1, 'no']]
labels = ['no surfacing','flippers']
#change to discrete values
return dataSet, labels接下来我们要通过第一部分计算经验熵的公式来计算熵,通过熵的计算公式可知,这里需要用到以2为底的对数log,所以在文件开头加上
from math import log具体计算熵的代码如下所示:
def calcShannonEnt(dataSet):
numEntries = len(dataSet)
labelCounts = {}
for featVec in dataSet: #the the number of unique elements and their occurance
currentLabel = featVec[-1]
if currentLabel not in labelCounts.keys(): labelCounts[currentLabel] = 0
labelCounts[currentLabel] += 1
shannonEnt = 0.0
for key in labelCounts:
prob = float(labelCounts[key])/numEntries
shannonEnt -= prob * log(prob,2) #log base 2
return shannonEnt参考文献:
1、《统计学习方法》李航 著
2、《机器学习实战》
3、《信息论》