【轻量级网络】Octave Convolution

Paper：Octave Convolution
Github：Offical 和 UnOffical

Octave是指八音阶，在音乐中降低八音阶代表频率减半。

Abstract

自然图像中的信息可以被分解为低频信息和高频信息，低频信息通常是全局结构而高频信息通常是细节信息。类似，卷积的输出特征图也可看作是低频信息和高频信息的混合。

Ocave Convolution将特征图进行分解，从而消耗更少的内存和计算资源。另外OctConv通过对低频信息的特殊处理，扩大了感受野，提高了识别效果。

Octave Convolution

CNNs在很多计算机视觉任务上已经取得了很大的成功。目前主要通过较少参数冗余和特征图的channel数来解决。然而特征图在空间上也存在冗余，每一个位置独立存储特征，忽略了相邻位置的公共信息，事实上这些信息可一起存储处理。

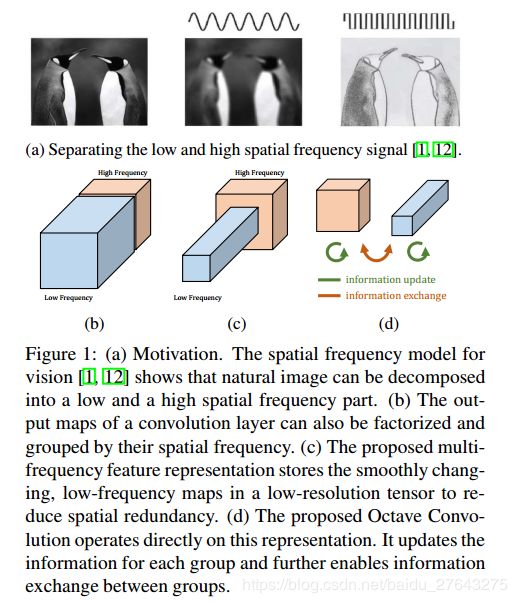
低频信息变化缓慢，信息量少
高频信息变化剧烈，信息量多

通过相邻位置间的信息共享，可减小低频信息组的空间分辨率，从而有效扩大感受野。

通过将卷积特征图分为高频和低频两组，同时对低频部分的信息进行压缩，可以减少空间的信息冗余。

OctConv是一种即插即用式卷积，不需要修改网络结构或进行超参数调整。

Architecture

低频组的特征分辨率只有高频组分辨率的一半

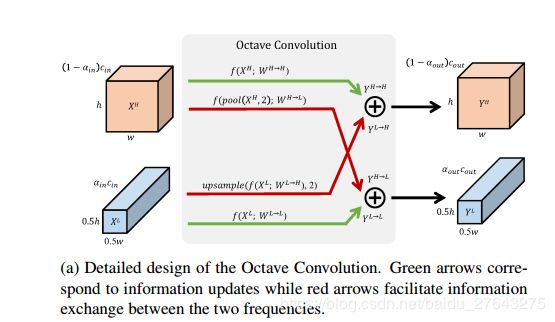
高频信息：
$Y_{p,q}^H=Y_{p,q}^{H\to H}+Y_{p,q}^{L\to H}$$$=\sum _{i,j\in {\mathcal{N}}_k}{W}_{i+\frac{k-1}{2},j+\frac{k-1}{2}}^{H\to H}{}_{j+\frac{k-1}{2}}^{\top }{X}_{p+i,q+j}^H+\sum _{i,j\in {\mathcal{N}}_k}{W}_{i+\frac{k-1}{2},j+\frac{k-1}{2}}^{L\to H}{X}_{\left(\lfloor \frac{p}{2}]+i\right),\left(\lfloor \frac{q}{2}\rfloor +j\right)}$$
低频信息：
$Y_{p,q}^L=Y_{p,q}^{L\to L}+Y_{p,q}^{H\to L}$$$=\sum _{i,j\in {\mathcal{N}}_k}{W}_{i+\frac{k-1}{2},j+\frac{k-1}{2}}^{L\to L}{,}_{j+\frac{k-1}{2}}^{\top }{X}_{p+i,q+j}^L+\sum _{i,j\in {\mathcal{N}}_k}{W}_{i+\frac{k-1}{2},j+\frac{k-1}{2}}^{H\to L}{X}_{(2\ast p+0.5+i),(2\ast q+0.5+j)}^H$$

文中分析了两种降采样方式：stride convolution与average pooling。最终采取了后者。因为如图所示，stride convolution会造成一定程度上特征偏移，带特征融合中造成特征不对齐，进而影响性能。

上式可简化为：

$$\begin{array}{rl}{Y}^H& =f\left(X^H;W^{H\to H}\right)+\text{ upsample }(f\left(X^L;W^{L\to H}\right)\\ Y^L& =f\left(X^L;W^{L\to L}\right)+f\left(\mathrm{pool}\left(X^H,2\right);W^{H\to L}\right))\end{array}$$

pool(X, k) is an average pooling operation with kernel size k × k and stride k. upsample(X, k) is an up-sampling operation by a factor of k via nearest interpolation.

Experimental Evaluation

精度相同的情况下，OctConv的FLOPs大大减少。

参考：https://blog.csdn.net/weixin_37993251/article/details/89333099#commentBox