算法：编辑距离问题（动态规划）

问题描述：

                

设A和B是2个字符串。要用最少的字符操作将字符串A转换为字符串B。这里所说的字符操作包括(1)删除一个字符； (2)插入一个字符； (3)将一个字符改为另一个字符。将字符串A变换为字符串B所用的最少字符操作数称为字符串A到 B的编辑距离，记为d(A,B)。对于给定的字符串A和字符串B，计算其编辑距离 d(A,B)。

个人对问题的理解：设两个字符串s[0:i],t[0:j]，用最少的操作数（三种：增删换，三种各花销一次操作）将s变成t（或者t变成s，同等），先解决三种特殊情况

1）s为空，t不为空；

2）t为空，s不为空；

3）s与t相等；

对于第一第二种情况，即在i等于0时，也就是说s为空，增加j个字符，使得s转化为t，在j等于0时，也就是说t为空，就是减少 i个字符，使得s转化为t。

对于第三种情况，显然为d(A,B)=0。

算法描述：

                

1）现在只剩下普通（一般）情况，运用动态规划求出递归方程，将原问题分解为若干个子问题进行求最优解，后得出原问题的最优解，采用“填表的方法”，设计步骤：对每个子问题只求解一次，将其结果保存在一张表（构造一个行数为n+1 列数为 m+1 的矩阵 , 用来保存完成某个转换需要执行的最少操作的次数)中。然后三步a.描述最优解的结构b.递归定义最优解的值c.按自底向上的方式计算最优解的值d.由计算出的结构构造一个最优解，利用解决子问题的最优值从而得出原问题的最优值。

2)矩阵设为d[i][j]，保存从S[0:i]变到t[0:j]的编辑距离。这里S[0:i]变到t[0:j]有三种情况，要求出这三种情况的最小值作为最小操作数。分别为：

（1）设可以在k1个操作内将s[0：i-1]转换为t[0：j]，用k1+1次操作将s[0：i]转化为t[0：j]，只需要先在“s[0：i]转化为t[0：j]”的操作开端做1次移除操作移除s[i]将s[0:i]转化为s[0:i-1]，然后再做k1个操作就可以转换为t[0:j]。对应表格，既矩阵所求d[i][j]的左格。

（2）设可以在k2个操作内将s[0：i]转换为t[0：j-1]，用k2+1次操作将s[0：i]转化为t[0：j]，先用k2次操作将s[0:i]转化为t[0：j-1]，然后再执行1次插入操作在“s[0:i]变成t[0：j-1]的操作”的末尾插入“增加t[j]”的一次操作，即可将s[0:i]转化为t[0:j]。对应表格，既矩阵所求d[i][j]的上格。

（3）设可以在k3个操作内将s[0：i-1]转化为t[0：j-1] ，若s[i]==t[j]，S[0:i]变到t[0:j]就只要k3个操作，若s[i]！=t[j]，则需1次换操作加在s[0：i-1]转化为t[0：j-1]的操作数基础上就可以将S[0:i]变到t[0:j]，共k3+1次。对应所求d[i][j]的左上格。

即：（注释）

 

     子问题标识符的含义：从S[0:i]变到t[0:j]的编辑距离。(1<=i<=m,1<=j<=n)

     子问题递归公式：

      n   (m == 0 ) ;（n为字符串t的长度，m为字符串s的长度）

　　  m    (n== 0 )  ;

     d[j][i] =Math.min(d[j-1][i-1]+1,Math.min(d[j][i-1] + 1,d[j-1][i] + 1 ))   （s.charAt(i-1)!=t.charAt(j-1)）  1<=i<=m,1<=j<=n//java编写

     d[j][i] =Math.min(d[j-1][i-1],Math.min(d[j][i-1] + 1,d[j-1][i] + 1 ))   （s.charAt(i-1)==t.charAt(j-1)）  1<=i<=m,1<=j<=n

     原问题最优解：  双重循环扫描完从S[0:i]变到t[0:j]后，即S[0:m]变到t[0:n],最优值为d[n][m]的编辑距离。

3）对于d[i][j]二维数组，可以开辟为d[n+1][m+1]，n为字符串t的长度，m为字符串s的长度。首先进行如下初始化：

 

再根据以上所说的三种方法来填表，完成后如图：

 

如图，最优值为d[n][m]即为所求两串的编辑距离。

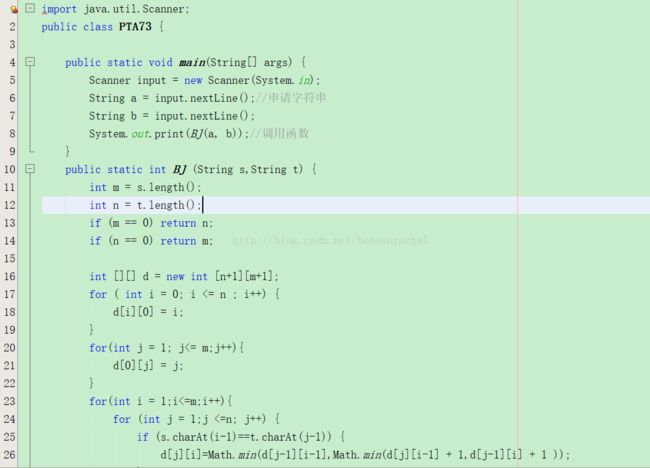
申请二维数组空间代码：

初始化代码：

 

扫描数组的代码（即解决每个子问题最终求得原问题解的过程的代码）：

结合上述所有情况：完整代码如下：

**注：//之前把当两个字符相同时直接定为d[j-1][i-1]，这个需不需要比较的问题，仍在讨论中，保险起见，暂时更改为上述做法。

算法时间及空间复杂度分析（此次为java编写）：

   由上述代码得，求子问题时的双重循环加两个初始化单循环的线性时间，再加上比较等操作的常数时间，得时间复杂度为O（M*N），而空间复杂度，花销了一个二维数组的辅助空间，得空间复杂度也为O（M*N）。

对于动态规划的问题，解决问题前得思考好各种可能出现的情况，并且写好三步：

      子问题标识符的含义：

      子问题递归公式：

      原问题最优解：

填表方法十分巧妙和便捷，得记牢此方法。