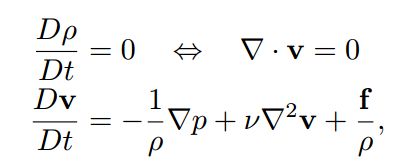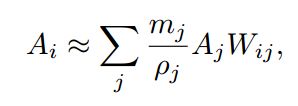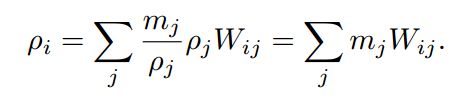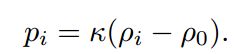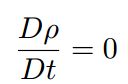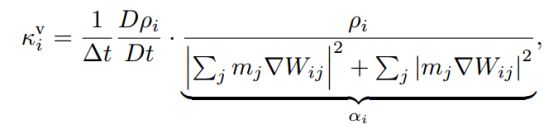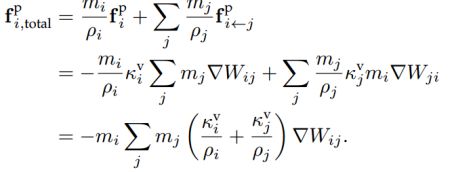基于物理流体模拟（PFSPH和DFSPH）

  本文主要介绍SPH流体模拟的一个实现库SPlishSPlasH用法这里 ，这是Blender和实验室提供的开源库，利用C++，OpenGL开发的。该库包含五种流行的SPH流体模拟方法（DFSPH[2],IISPH[4],PBF[5],PCISPH[3],PF[1]）和三种表面张力处理方法（Becker2007[6],Akinci2013[7],He2014[8]）和六种粘度项处理方法（standard[9]XSPH[10],Bender2017[2],Peer2015[11],Peer2016[12]）和两种旋度处理方法（MicropolarModel_Bender2017[13],VorticityConfinement[16]）以及两种DragForce(Macklin2014[14],Gissler2017[15]).将文章放在参考文献中，方便大家查看。

实现动画截图

                                

环境配置 

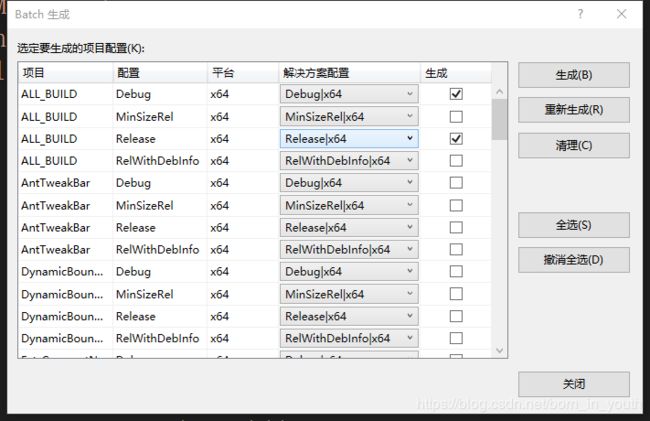
需要在Cmake软件中生成工程文件（选择好自己使用的VS版本），此时生成一个build文件夹，用VS打开里面的SPlishSPlasH解决方案，生成->批生成，如下图选择debug和release点击生成。此时应该有一个文件中有问题就是GPU平行计算语句

#pragma omp parallel sections

，点开这个文件为其加上一个头文件

#include 

就正常了（我当时没有截图，所以忘了具体出错的文件）

生成执行文件 

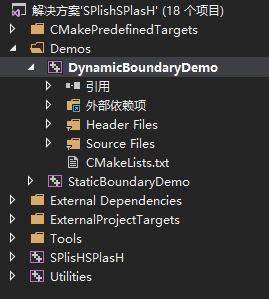
       工程刚打开时，默认的启动项是SPlishSPlasH静态库，需要将Demos下的Dynamic或者Static的项目设置成启动项，鼠标右键可以设置，因为在这两个项目中有入口函数main。

文件或函数介绍 

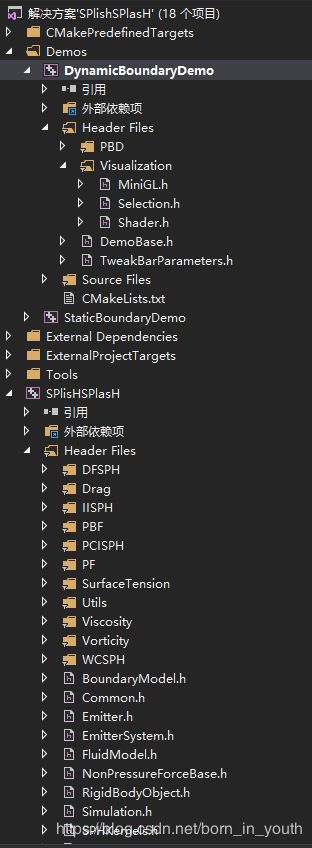
1.MiniGL.h(.cpp)是一个小型的opengl库，可以绘制cube、mesh、point、vector等。

2.Shader.h(.cpp)是一个着色器程序，包含shader开档和灌uniform函数。是后续编写vertex和fragment着色器的基础。

3.Demobase.h(.cpp)中包含buildModel()和renderFluid()函数，以及设置exepath,datapath,sceneFilePath等。

           在init()函数中修改场景.json文件可以替换输入的模型

m_sceneFile = getDataPath() + "/Scenes/DamBreakModel.json";

D:\···\SPlisHSPlasH-master\data\Scenes 在这个文件上有作者提供的模型.json数据传输文件，也可以用VS编写自己的.json导入自己需要的模型

     在renderFluid()函数中可以更改渲染设置，输入自己想要的颜色和uniform。

4.PoissonDiskSampling.h(.cpp)是复杂形变表面采样文档

5.Partio库是C++库轻松读写操作。常见粒子动画中

6.AntTweakBar库是界面库（便于用户交互操作参数）

7.Simulation.h(.cpp)是N-S方程计算

ProjectiveFluid(PF)模拟方法

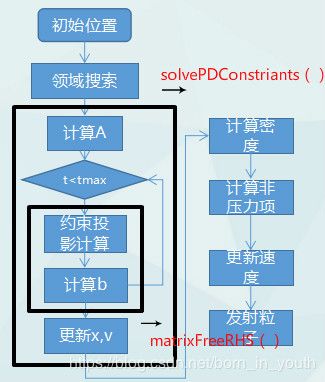
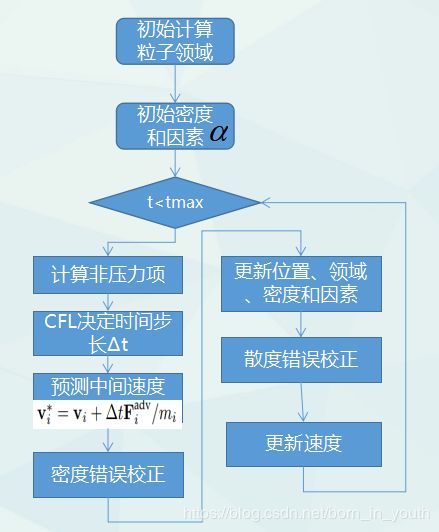
Weiler[1]第一次将用于模拟布料和柔体的并行性很高的Projective Dynamic方法引入到流体模拟中称之为Projective Fluid(PF)，使得流体模拟方法更丰富和快速。该方法流体约束条件是基于粒子压力与密度关系的equation of state(EOS)推导而得。算法流程以及各部分计算所在函数如下图。

                                                                    

 Divergence-Free SPH[2]模拟方法

          DFSPH方法将隐士压力解决方案和散度自由的速度场相结合，增加模拟稳定性，可以使用长时间步长。保证液体的不可压缩性，通过散度自由和恒定密度条件共同决定。从速度和密度水平两方面考虑不可压缩性。因为在计算密度等数值时间积分会造成数值错误随着时间会累积，A的计算，所以加上一条密度恒定条件可以抵消误差。

           算法流程：

                                                   

 

             算法原理：

     本文建模方式是依据欧拉视角建模的，每个粒子水滴数值不变（密度，速度，压强）只是移动。拉格朗日的视角中没有改变

1.不可压缩的N-S方程

方程一，散度自由的速度域

本文模拟低粘度的水，所以将方程二等式右边第二项粘度计算忽略。

本文通过执行散度自由条件方程一和恒定密度条件方程三来满足方程一不可压缩条件。两条件是通过计算刚度系数和对应压力解决的。

由此公式可以推导出方程一的充分必要条件转换。

2.SPH计算

A代表粒子在位置x的属性（速度/密度/压强等），计算公式如下：

核函数：

同理，密度计算公式：

压强：为静止压强。

  压强用于计算压力，压力可以抵消密度差值，

1. 散度自由方案

A.目标：保证

B.输入：

C.过程：依据速度和影响因素计算刚度系数

其中，

依据刚度系数计算粒子i的总压力

然后计算更新粒子的速度。

D.原理：粒子i当前的散度错误使用散度的SPH公式确定：[6]

可以推导出刚度系数。通过这种方法计算的刚度系数，再来计算压力可以保证散度自由。

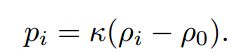
由这两个公式可以看出压力与刚度系数有关，而刚度系数的计算是通过粒子的散度错误那部分决定的，所以可以弥补。

2.恒定密度方案

目标：最小化差值。

输入：由非压力项的力（重力、表面张力）决定的速度和预先计算的影响因素

循环条件：流体活跃粒子平均密度与原始流体粒子密度的差，和迭代最大次数共同制约。

过程：纠正密度错误通过计算压力。依据速度和影响因素计算刚度系数，依据刚度系数计算粒子i的总压力，然后计算更新粒子的速度。

原理：同散度自由方案一样，这里将用到的刚度系数，通过粒子当前散度错误确定的散度公式计算的密度来确定刚度系数，静儿计算压力值，所以可以避免密度差值。

 

   参考文献

1. Weiler, Marcel ; Koschier, Dan ; Bender, Jan :Projective Fluids.[Online-Edition: http://doi.acm.org/10.1145/2994258.2994282] In: Proceedings of the 9th International Conference on Motion in Games. MIG '16. ACM, New York, NY, USA New York, NY, USA , pp. 79-84. ISBN 978-1-4503-4592-7 [Buchkapitel], (2016).
2. Bender J, Koschier D:Divergence-Free SPH for Incompressible and Viscous Fluids,IEEE Trans Vis Comput Graph. 2017 Mar;23(3):1193-1206. doi: 10.1109/TVCG.2016.2578335. Epub 2016 Jun 8.
3. B. Solenthaler and R. Pajarola, “Predictive-corrective incompressible SPH,” ACM Transactions on Graphics, vol. 28, no. 3, pp. 40:1–40:6, 2009.
4. M. Ihmsen, J. Cornelis, B. Solenthaler, C. Horvath, and M. Teschner, “Implicit incompressible SPH,” IEEE Transactions on Visualization and Computer Graphics, vol. 20, pp. 426–435, 2014.
5. M. Macklin and M. Muller, “Position Based Fluids,” ¨ ACM Transactions on Graphics, vol. 32, no. 4, pp. 1–5, 2013.
6. M. Becker and M. Teschner, “Weakly compressible SPH for free surface flows,” in ACM SIGGRAPH / Eurographics Symposium on Computer Animation, 2007, pp. 1–8.
7. N. Akinci, G. Akinci, and M. Teschner, “Versatile surface tension and adhesion for SPH fluids,” ACM Transactions on Graphics,vol. 32, no. 6, pp. 1–8, 2013.
8. HE, X., WANG, H., ZHANG, F., WANG, H., WANG, G., AND ZHOU, K. 2014. Robust Simulation of Sparsely Sampled Thin Features in SPH-Based Free Surface Flows. ACM Trans. On Graphics 34, 1, 7:1–7:9.
9. Markus Ihmsen, Jens Orthmann, Barbara Solenthaler, Andreas Kolb, and Matthias Teschner. SPH Fluids in Computer Graphics. In Sylvain Lefebvre and Michela Spagnuolo, editors, Eurographics 2014 - State of the Art Reports. The Eurographics Association, 2014.
10. Hagit Schechter and Robert Bridson. Ghost sph for animating water. ACM Trans. Graph., 31(4):61:1–61:8, July 2012.
11. A. Peer, M. Ihmsen, J. Cornelis, and M. Teschner. An Implicit Viscosity Formulation for SPH Fluids. ACM Trans. Graph., 34(4):1–10, 2015.
12. Andreas Peer and Matthias Teschner. Prescribed velocity gradients for highly viscous SPH fluids with vorticity diffusion. IEEE Transactions on Visualization and Computer Graphics, pages 1–9,1.
13. Jan Bender, Dan Koschier, Tassilo Kugelstadt, and Marcel Weiler. A micropolar material model for turbulent sph fluids. In Proceedings of the 14th ACM SIGGRAPH / Eurographics Symposium on Computer Animation, SCA '17. ACM, 2017.
14. Miles Macklin, Matthias Müller, Nuttapong Chentanez, and Tae-Yong Kim. Unified Particle Physics for Real-Time Applications. ACM Trans. Graph., 33(4):1–12, 2014.
15. Christoph Gissler, Stefan Band, Andreas Peer, Markus Ihmsen, and Matthias Teschner. Approximate air-fluid interactions for sph. In Virtual Reality Interactions and Physical Simulations, pages 1–10, April 2017.
16. Miles Macklin and Matthias Müller. Position based fluids. ACM Trans. Graph., 32(4):104:1–104:12, July 2013.