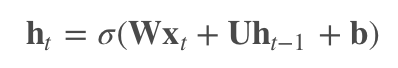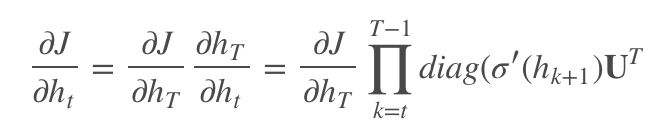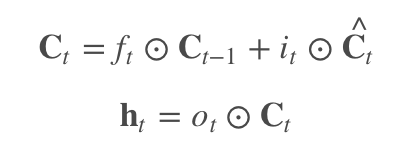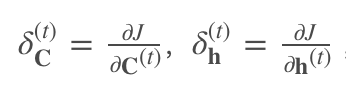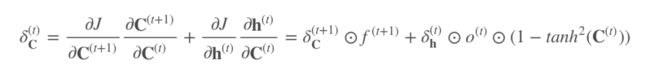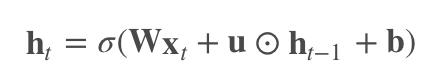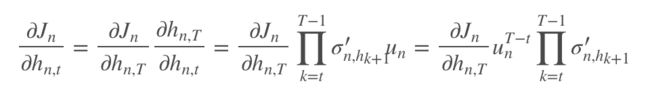新型RNN:将层内神经元相互独立以提高长程记忆 | CVPR 2018论文解读
在碎片化阅读充斥眼球的时代,越来越少的人会去关注每篇论文背后的探索和思考。
在这个栏目里,你会快速 get 每篇精选论文的亮点和痛点,时刻紧跟 AI 前沿成果。
点击本文底部的「阅读原文」即刻加入社区,查看更多最新论文推荐。
这是 PaperDaily 的第 58 篇文章本期推荐的论文笔记来自 PaperWeekly 社区用户 @Zsank。本文使用 Relu 等非饱和激活函数使网络变得更具有鲁棒性,可以处理很长的序列(超过5000个时间步),可以构建很深的网络(实验中用了21层)。在各种任务中取得了比LSTM更好的效果。
如果你对本文工作感兴趣,点击底部的阅读原文即可查看原论文。
关于作者:麦振生,中山大学数据科学与计算机学院硕士生,研究方向为自然语言处理和问答系统。
■ 论文 | Independently Recurrent Neural Network (IndRNN): Building A Longer and Deeper RNN
■ 链接 | https://www.paperweekly.site/papers/1757
■ 源码 | https://github.com/batzner/indrnn
论文亮点
传统 RNN 因为在时间上参数共享,所以会出现梯度消失/爆炸问题。LSTM/GRU 在解决层内梯度消失/爆炸问题时,梯度仍然会在层间衰减,所以 LSTM/GRU 难以做成多层网络。并且,LSTM/GRU 也存在着无法捕捉更长的时序信息的问题。
此外,传统 RNN 由于层内神经元相互联系,难以对神经元的行为进行合理的解释。
基于上述问题,论文提出了 IndRNN,亮点在于:
1. 将 RNN 层内神经元解耦,使它们相互独立,提高神经元的可解释性。
2. 有序列表能够使用 Relu 等非饱和激活函数,解决层内和层间梯度消失/爆炸问题,同时模型也具有鲁棒性。
3. 有序列表比 LSTM 能处理更长的序列信息。
模型介绍
论文模型比较简单。介绍模型前,我们先来理一下 RNN 梯度的有关知识。
RNN梯度问题
先来看 RNN 隐状态的计算:
设 T 时刻的目标函数为 J,则反向传播时到 t 时刻的梯度计算:
其中 diag(σ′(hk+1) 是激活函数的雅可比矩阵。可以看到,RNN 的梯度计算依赖于对角矩阵 diag(σ′(hk+1))U^T 的连积,即求该对角阵的 n 次幂。
对角元素只要有一个小于 1,那么 n 次乘积后会趋近于 0;
对角元素只要有一个大于 1,那么 n 次乘积后会趋近无穷大。
RNN 常用的两种激活函数,tanh 的导数为 1−tanh2 ,最大值为 1,图像两端趋于 0;sigmoid 的导数为 sigmoid(1−sigmoid) ,最大值为 0.25,图像两端趋于 0。
可见两种激活函数的导数取值绝大部分小于 1。因此它们与循环权重系数相乘构成的对角矩阵元素绝大部分小于 1(可能会有等于 1 的情况,但不会大于 1),连积操作会导致梯度指数级下降,即“梯度消失”现象。对应第一种情况。
而在 RNN 中使用 Relu 函数,由于 Relu 在 x>0 时导数恒为 1,因此若 U 中元素有大于 1 的,则构成的对角矩阵会有大于 1 的元素,连积操作会造成梯度爆炸现象。对应第二种情况。
解决方案
门控函数(LSTM/GRU)
引入门控的目的在于将激活函数导数的连乘变成加法。以 LSTM 为例:
反向传播时有两个隐态:
其中仅 C(t) 参与反向传播:
加号后的项就是 tanh 的导数,这里起作用的是加号前的项, f(t+1) 控制着梯度衰减的程度。当 f=1 时,即使后面的项很小,梯度仍能很好地传到上一时刻;f=0 时,即上一时刻的信号对此刻不造成任何影响,因此可以为 0。
门控函数虽然有效缓解了梯度消失的问题,但处理很长序列的时候仍然不可避免。尽管如此,LSTM/GRU 在现有 NLP 任务上已经表现很好了。论文提出门控函数最主要的问题是门的存在使得计算过程无法并行,且增大了计算复杂度。
并且,在多层 LSTM 中,由于还是采用 tanh 函数,在层与层之间的梯度消失仍然没有解决(这里主要是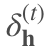 的影响),所以现阶段的多层 LSTM 多是采用 2~3 层,最多不会超过 4 层。
的影响),所以现阶段的多层 LSTM 多是采用 2~3 层,最多不会超过 4 层。
初始化(IRNN)
Hinton 于 2015 年提出在 RNN 中用 Relu 作为激活函数。Relu 作为激活函数用在 RNN 中的弊端在前面已经说明了。为了解决这个问题,IRNN 将权重矩阵初始化为单位矩阵并将偏置置 0(IRNN的 I 因此得名——Identity Matrix)。
此后,基于 IRNN,有人提出了改进,比如将权重矩阵初始化为正定矩阵,或者增加正则项。但 IRNN 对学习率很敏感,在学习率大时容易梯度爆炸。
梯度截断
在反向传播中,梯度消失/爆炸前会有一个渐变的过程。梯度截断的意思就是,在渐变过程中,人为设定只传递几步,即人为设定对角矩阵连乘几次,然后强行拉回正常值水平,再进行梯度下降。该方法对解决梯度问题比较有效,但总有人为的因素,且强行拉回的值不一定准确。有没有更优雅的方法呢?
IndRNN
为了解决梯度消失/爆炸问题,IndRNN 引入了 Relu 作为激活函数,并且将层内的神经元独立开来。对 RNN 的式子稍加改进,就变成了 IndRNN:
权重系数从矩阵 U 变成了向量 u 。⊙ 表示矩阵元素积。也即在 t 时刻,每个神经元只接受此刻的输入以及 t-1 时刻自身的状态作为输入。
而传统 RNN 在 t 时刻每一个神经元都接受 t-1 时刻所有神经元的状态作为输入。所以 IndRNN 中的每个神经元可以独立地处理一份空间 pattern,可视化也就变得可行了。 现在来看一下梯度问题:
与传统 RNN 的梯度作对比,可以发现此时的连积操作不再是矩阵操作,而是将激活函数的导数与循环权重系数独立起来,使用 Relu 作为激活函数也就顺理成章了。至此,梯度问题完美解决(作者在论文里有详细的推导过程)。
神经元之间的相互连接依赖层间交互来完成。也就是说,下一层的神将元会接受上一层所有神经元的输出作为输入(相当于全连接层)。
作者在论文里证明了两层的 IndRNN 相当于一层激活函数为线性函数、循环权重为可对角化矩阵的传统 RNN。
IndRNN 可实现多层堆叠。因为在多层堆叠结构中,层间交互是全连接方式,因此可以进行改进,比如改全连接方式为 CNN 连接,也可引入 BN、残差连接等。
实验介绍
实验部分首先在三个评估 RNN 模型的常用任务上进行,以验证 IndRNN 的长程记忆能力和深层网络训练的可行性,为验证性实验。然后在骨骼动作识别任务上进行预测,为实验性实验。
Adding Problem
任务描述:输入两个序列,第一个序列是一串在(0,1)之间均匀采样的数字,第二个序列是一串同等长度的、其中只有两个数字为 1,其余为 0 的数字,要求输出与第二个序列中两个数字 1 对应的第一个序列中的两个数字的和。
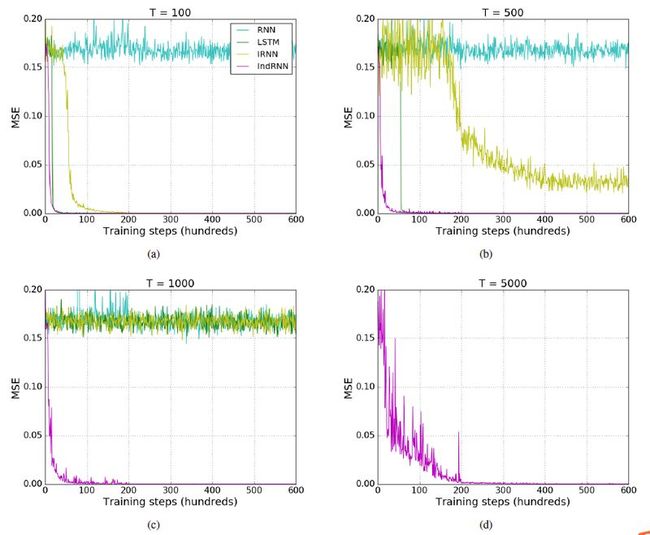
实验的序列长度分别为 100,500 和 1000,采用 MSE 作为目标函数。
实验结果可以看出,IRNN 和 LSTM 都只能处理中等长度的序列(500-1000步),而 IndRNN 可以轻松处理时间跨度 5000 步的序列数据。
Sequential MNIST Classification
任务描述:输入一串 MINIST 像素点的数据,然后进行分类。而 pMINIST 则在 MINIST 任务上增加了难度:像素点数据进行了置换。
Language Modeling
任务描述:在字符级别 PTB 数据集上进行语言模型的评估。在该任务中,为了验证 IndRNN 可以构造深层网络,论文里给出了 21 层 IndRNN 的训练以及结果。
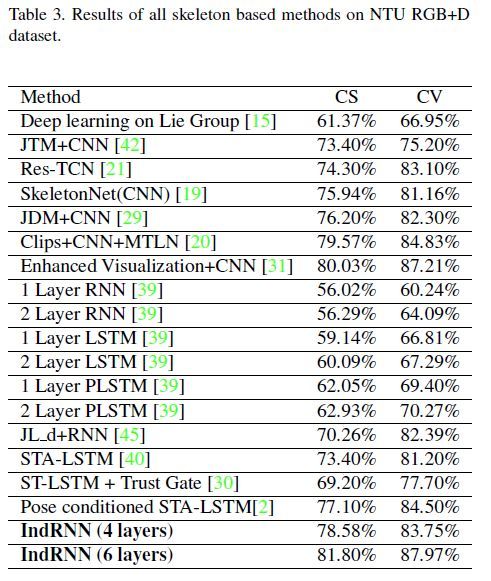
Skeleton Based Action Recognition
任务描述:使用了 NTU RGB+D 的数据库,是目前为止最大的基于骨骼的动作识别数据库。
个人心得
论文里将层内神经元独立开来的想法虽然看似简单,但要想出来还真的不容易。本文为理解 RNN 提供了一个新的角度,也让 RNN 单个神经元行为的解释变得可行。此外,Relu 函数的使用也使得 RNN 堆叠结构成为可能。
从实验结果来看,IndRNN 带来的效果提升都比较显著。但有一点是,Relu 函数可能会输出 0,在序列数据里意味着之前的历史信息全部丢弃。是否换成 Leaky Relu 会更好一点?
本文由 AI 学术社区 PaperWeekly 精选推荐,社区目前已覆盖自然语言处理、计算机视觉、人工智能、机器学习、数据挖掘和信息检索等研究方向,点击「阅读原文」即刻加入社区!
![]()
点击标题查看更多论文解读:
CycleGAN:图片风格,想换就换
基于GAN的字体风格迁移
基于置信度的知识图谱表示学习框架
基于文档级问答任务的新注意力模型
投稿须知 | 让你的文字被很多很多很多人看到
我是彩蛋
解锁新功能:热门职位推荐!
PaperWeekly小程序升级啦
今日arXiv√猜你喜欢√热门职位√
找全职找实习都不是问题
解锁方式
1. 识别下方二维码打开小程序
2. 用PaperWeekly社区账号进行登陆
3. 登陆后即可解锁所有功能
职位发布
请添加小助手微信(pwbot02)进行咨询
长按识别二维码,使用小程序
*点击阅读原文即可注册
关于PaperWeekly
PaperWeekly 是一个推荐、解读、讨论、报道人工智能前沿论文成果的学术平台。如果你研究或从事 AI 领域,欢迎在公众号后台点击「交流群」,小助手将把你带入 PaperWeekly 的交流群里。
▽ 点击 | 阅读原文 | 查看原论文