触动人生

EM算法--二维高斯混合模型(GMMs)

参考文章

http://blog.163.com/baolong_zhu/blog/static/196311091201421185531966/

《统计学习方法》李航

EM算法是一种迭代算法，1977年由Dempster等人总结出，用于含有隐变量的概率模型参数的极大似然估计，或极大后验概率估计。EM算法的每次迭代由两步组成：E步，求期望(expectation);M步，求极大(maximization).所以这一算法称为期望极大算法(expectation maximization algorithm),简称EM算法。

首先准备一些预备知识，如：二维高斯混合函数的形式，协方差的定义

高斯混合函数

对于一维混合高斯函数，如(1)式所示。(所谓的混合高斯，就是将一些高斯函数利用一些权值系数组合起来) （1）

二维高斯混合函数，如(2)式所示。

（2）

可以看出二维高斯混合模型，其中的d为数据的维度，在这里等于2；∑ 代表协方差矩阵，两行两列；这里的x以及μ都是二维的数据，用矩阵表示就是一行两列。这里提到了协方差矩阵，那么什么是协方差矩阵，与方差有什么区别？

协方差矩阵

理解协方差矩阵的关键在于牢记它计算的是不同维度之间的协方差，而不是不同样本之间。拿到一个样本矩阵，我们最先明确的是一行是一个样本还是一个维度（重要）。

方差表示的是每个样本值与全体样本值的平均数之差的平方值的平均数，反映了一组数据的离散程度。

既然有了方差还要协方差干啥？显然，方差只能衡量一维数据的离散程度，对于二维数据，就用到了协方差，如下式所示。其中X，Y代表一组数据的两个维度。COV(X,Y)的值大于零，表示两个维度的数据成正相关，小于零则表示成负相关，等于零表示两个维度的数据相互独立。显然当X=Y时，COV(X,X)计算的就是方差。由协方差的定义可以得到COV(X,Y)=COV(Y,X)。

二维数据的协方差矩阵表示为，显然协方差矩阵为对角矩阵。

三维数据的协方差矩阵表示为，同理知道N维数据的协方差矩阵。

EM算法

假设一组数据x1,x2,...,xn是来自上述二维高斯混合模型，这里我们利用EM算法确定各个高斯部件的参数，充分拟合给定的数据。算法目的具体的理论知识与算法步骤参考《统计学习方法》李航一书中对于EM算法的讲解(李航的这一本书，绝对值得学习)。

我主要写一下自己的理解，也为自己以后复习用。

EM算法其实就是概率模型参数的极大似然估计法，只不过存在一些隐变量，从而不能像一般的概率模型参数估计一样直接求似然函数的最大值，因为这里的似然函数存在隐变量，因而不存在解析解，就不能直接对似然函数求偏导来求极大值，只能迭代求解。

基本思想：

E步，假设参数已知，去估计隐藏变量的期望；

M步，利用E步求得的隐藏变量的期望，根据最大似然估计求得参数，然后新得到的参数值重新被用于E步。。。直至收敛到局部最优解。

需要注意的一点是：理论中，E步最重要的是求Q函数（李航 9.29式），即完全数据的对数似然函数的期望，M步要做的是用Q函数对各参数求偏导，从而确定满足Q函数最大的各参数的值。而在程序中，因为M步Q函数对参数求偏导后，各参数的值由Q函数中的Gamma(j,k)决定，所以E步只需计算Gamma(j,k)即可，Gamma(j,k)代表第j个样本属于第k个高斯模型的概率，这样M步各参数的值也就确定了，所以切记实例理论与程序实现的区别，好像是程序只是利用了理论的精简结果。

学习完理论之后，最好写个程序练习一下，加深自己的理解。下面的程序(matlab编写)，是这样一个过程：

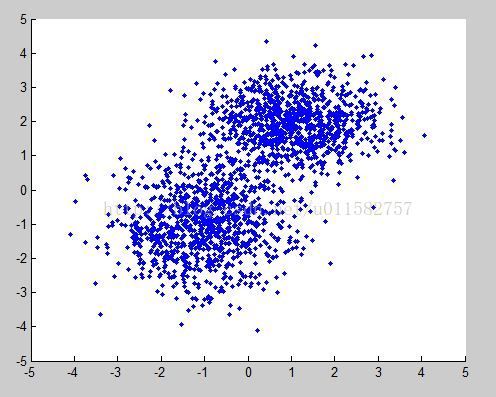
1.首先产生两组数据点。每一组数据点都是符合给定均值Mu和协方差矩阵∑的。程序和图如下所示，

%产生2个二维正态数据
MU1 = [1 2];
SIGMA1 = [1 0; 0 0.5];
MU2 = [-1 -1];
SIGMA2 = [1 0; 0 1];
X = [mvnrnd(MU1, SIGMA1, 1000);mvnrnd(MU2, SIGMA2, 1000)];
scatter(X(:,1),X(:,2),10,'*');

2.对于上述产生的数据，利用EM算法预测这组数据对应的均值μ和协方差矩阵∑

对于各参数初值的设置：两个均值初始值各设置为两组数据点中的随机一个样本点，权值系数初始值设置为1/k,k是高斯混合模型中模型的个数，协方差矩阵初值设置为所有数据的协方差。

程序：GMM.m

%程序中Psi对应二维高斯函数，其中的(x-μ)与其转置的顺序与上述提到的高斯函数不同，这样是为了保证矩阵可乘性，不影响结果.
%Gamma 为隐变量的值，Gamma(i,j)代表第i个样本属于第j个模型的概率。
%Mu为期望，Sigma为协方差矩阵%Pi为各模型的权值系数%产生2个二维正态数据
%产生2个二维正态数据
MU1 = [1 2];
SIGMA1 = [1 0; 0 0.5];
MU2 = [-1 -1];
SIGMA2 = [1 0; 0 1];
%生成1000行2列(默认)均值为mu标准差为sigma的正态分布随机数
X = [mvnrnd(MU1, SIGMA1, 1000);mvnrnd(MU2, SIGMA2, 1000)];
%显示
scatter(X(:,1),X(:,2),10,'.');
%====================
K=2;
[N,D]=size(X);
Gamma=zeros(N,K);
Psi=zeros(N,K);
Mu=zeros(K,D);
LM=zeros(K,D);
Sigma =zeros(D, D, K);
Pi=zeros(1,K);
%选择随机的两个样本点作为期望迭代初值
Mu(1,:)=X(randint(1,1,[1 N/2]),:);
Mu(2,:)=X(randint(1,1,[N/2 N]),:);
%所有数据的协方差作为协方差初值
for k=1:K
Pi(k)=1/K;
Sigma(:, :, k)=cov(X);
end
LMu=Mu;
LSigma=Sigma;
LPi=Pi;
while true
%Estimation Step
for k = 1:K
Y = X - repmat(Mu(k,:),N,1);
Psi(:,k) = (2*pi)^(-D/2)*det(Sigma(:,:,k))^(-1/2)*diag(exp(-1/2*Y/(Sigma(:,:,k))*(Y'))); %Psi第一列代表第一个高斯分布对所有数据的取值
end
Gamma_SUM=zeros(D,D);
for j = 1:N
for k=1:K
Gamma(j,k) = Pi(1,k)*Psi(j,k)/sum(Psi(j,:)*Pi'); %Psi的第一行分别代表两个高斯分布对第一个数据的取值
end
end
%Maximization Step
for k = 1:K
%update Mu
Mu_SUM= zeros(1,D);
for j=1:N
Mu_SUM=Mu_SUM+Gamma(j,k)*X(j,:);
end
Mu(k,:)= Mu_SUM/sum(Gamma(:,k));
%update Sigma
Sigma_SUM= zeros(D,D);
for j = 1:N
Sigma_SUM = Sigma_SUM+ Gamma(j,k)*(X(j,:)-Mu(k,:))'*(X(j,:)-Mu(k,:));
end
Sigma(:,:,k)= Sigma_SUM/sum(Gamma(:,k));
%update Pi
Pi_SUM=0;
for j=1:N
Pi_SUM=Pi_SUM+Gamma(j,k);
end
Pi(1,k)=Pi_SUM/N;
end

R_Mu=sum(sum(abs(LMu- Mu)));
R_Sigma=sum(sum(abs(LSigma- Sigma)));
R_Pi=sum(sum(abs(LPi- Pi)));
R=R_Mu+R_Sigma+R_Pi;
if ( R<1e-10)
disp('期望');
disp(Mu);
disp('协方差矩阵');
disp(Sigma);
disp('权值系数');
disp(Pi);
obj=gmdistribution(Mu,Sigma);
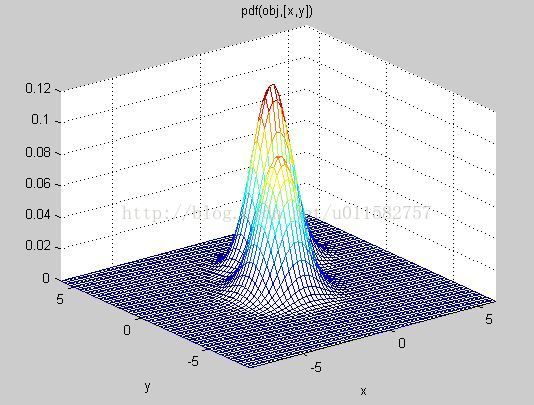
figure,h = ezmesh(@(x,y)pdf(obj,[x,y]),[-8 6], [-8 6]);
break;
end
LMu=Mu;
LSigma=Sigma;
LPi=Pi;
end
%=====================

%%%%%%%%运行结果%%%%%%%
%
% 期望
% 1.0334 2.0479
% -0.9703 -0.9879
%
% 协方差矩阵
%
% (:,:,1) =
%
% 0.9604 -0.0177
% -0.0177 0.4463
%
%
% (:,:,2) =
%
% 0.9976 0.0667
% 0.0667 1.0249
%
% 权值系数
% 0.4935 0.5065
%%%%%%%%%%%%%%%%%%%%%%%%%