决策树（Decision Tree）

一、简介

  决策树(decision tree)是一种基本的分类与回归方法。本章主要讨论用于分类的决策树。决策树模型呈树形结构，在分类问题中，表示基于特征对实例进行分类的过程。它可以认为是if-then规则的集合，也可以认为是定义在特征空间与类空间上的条件概率分布。其主要优点是模型具有可读性，分类速度快。学习时，利用训练数据，根据损失函数最小化的原则建立决策树模型。预测时，对新的数据，利用决策树模型进行分类。决策树学习通常包括3个步骤：特征选择、决策树的生成和决策树的修剪。

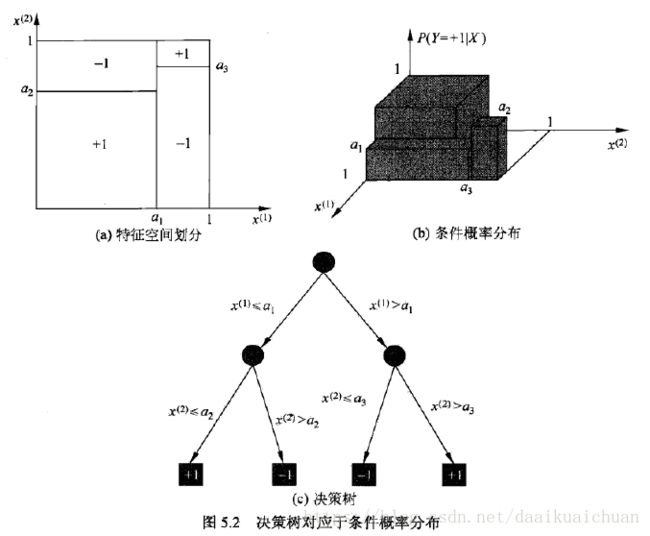
二、特征选择

  不同的决策树的特征选择方法各有不同，用于分类的树可以采用信息增益，信息增益比，基尼系数等，用于回归的树可以采用损失函数最小等等方法。

1、熵

  熵的大小是代表一个随机变量的不确定性大小，如果一个随机变量的概率分布如下：

P(X=xi)=pi,i=1,2,3…,n P ( X = x i ) = p i , i = 1 , 2 , 3 … , n

那么这个变量的熵为：

H(X)=−∑i=1npilogpi H ( X ) = − ∑ i = 1 n p i log ⁡ p i

对于一个binary变量(0,1),熵随其中某一值概率变化的曲线如下：

2、条件熵

  条件熵指的是当某变量已知的情况下随机变量的不确定性，如下：

H(Y|X)=∑i=1npiH(Y|X=xi) H ( Y | X ) = ∑ i = 1 n p i H ( Y | X = x i )

上式中 pi=P(X=xi),i=1,2,…,n p i = P ( X = x i ) , i = 1 , 2 , … , n 。

3、信息增益

  一个特征对于训练数据的信息增益指的是训练集合的经验熵与该特征给定的情况下的经验条件熵的差。如果一个熵是通过数据估计得到的，那么这个熵就是经验熵。 信息增益表示得知特征X的信息而使得Y的信息的不确定性减少的程度。

g(D,A)=H(D)−H(D|A) g ( D , A ) = H ( D ) − H ( D | A )

一般的这个差也被称之为互信息。在数的特征选择中会选择信息增益大的特征作为节点进行分类。

4、信息增益比

  由于采用信息增益作为特征选择的标准时，树会偏向于选择一些取值比较多的特征。为了解决这个问题可以采用信息增益比。信息增益比是该特征的信息增益与训练数据的关于该特征的熵的比值，如下:

gR(D,A)=g(D,A)HA(D) g R ( D , A ) = g ( D , A ) H A ( D )

上式中 HA(D)=−∑ni=1|Di|Dlog2|Di|D H A ( D ) = − ∑ i = 1 n | D i | D log 2 ⁡ | D i | D ，n为特征A取值个数。

5、基尼指数

  基尼指数用在分类树中，这种树是二叉树，类似于信息增益用于描述集合的不确定性。

Gini(p)=∑k=1Kpk(1−pk)=1−∑k=1Kp2k G i n i ( p ) = ∑ k = 1 K p k ( 1 − p k ) = 1 − ∑ k = 1 K p k 2

上式中K为类的个数，pk为属于每个类的概率。由于这种树是二叉树，所以某一特征条件给定的时候样本集合会被分割成两个部分，那么在该特征A的条件下，集合D的基尼指数为：

Gini(D,A)=|D1||D|Gini(D1)+|D2||D|Gini(D2) G i n i ( D , A ) = | D 1 | | D | G i n i ( D 1 ) + | D 2 | | D | G i n i ( D 2 )

在分类树的训练过程中会采用基尼指数最小的特征条件来作为节点。

三、决策树的生成

1、ID3算法

  ID3算法的核心是在决策树各个结点上应用信息增益准则选择特征。

2、C4.5算法

  C4.5对于ID3做了一些改进，将特征选取的依据从信息增益改成了信息增益比。

3、CART回归树

回归树每次采用平方误差最小作为选择节点条件的依据，不停的将样本集合分割成两个区域，直到满足停止条件为止。

4、CART分类树

回归树每次采用基尼指数作为选择节点条件的依据，不停的将样本集合分割成两个区域，直到满足停止条件为止。

四、决策树的剪枝

  剪枝是解决决策树过拟合的方法之一。

1、ID3与C4.5算法的剪枝

2、CART算法的剪枝

五、决策树的实现（ID3）

#include 
#include 
#include 
#include 
#include 
#include 
#include 
using namespace std;
#define MAXLEN 6//输入每行的数据个数  

//多叉树的实现   
//1 广义表  
//2 父指针表示法，适于经常找父结点的应用  
//3 子女链表示法，适于经常找子结点的应用  
//4 左长子，右兄弟表示法,实现比较麻烦  
//5 每个结点的所有孩子用vector保存  
//教训:数据结构的设计很重要，本算法采用5比较合适，同时  
//注意维护剩余样例和剩余属性信息，建树时横向遍历考循环属性的值，  
//纵向遍历靠递归调用  

vector<vector<string>> state;//实例集  
vector<vector<string>> state2;//实例集  
vector<string> item(MAXLEN);//对应一行实例集  
vector <string> attribute_row;//保存首行即属性行数据  
string end("end");//输入结束  
string yes("yes");  
string no("no");  
string blank("");  
map<string, vector<string >> map_attribute_values;//存储属性对应的所有的值
int tree_size = 0;  

struct Node//决策树节点
{
    string attribute;//属性值  
    string arrived_value;//到达的属性值  
    vector childs;//所有的孩子  
    Node()
    {
        attribute = blank;  
        arrived_value = blank;  
    }  
};  
Node * root;  

//根据数据实例计算属性与值组成的map  
void ComputeMapFrom2DVector()
{  
    unsigned int i,j,k;  
    bool exited = false;  
    vector<string> values;  
    for(i = 1; i < MAXLEN-1; i++)//按照列遍历  
    {
        for (j = 1; j < state.size(); j++)
        {  
            for (k = 0; k < values.size(); k++)
            {  
                if(!values[k].compare(state[j][i])) exited = true;  
            }
            if(!exited)
            {  
                values.push_back(state[j][i]);//注意Vector的插入都是从前面插入的，注意更新it，始终指向vector头  
            }
            exited = false;  
        }
        map_attribute_values[state[0][i]] = values;  
        values.erase(values.begin(), values.end());  
    }     
}  

//根据具体属性和值来计算熵  
double ComputeEntropy(vector<vector<string>> remain_state, string attribute, string value,bool ifparent)
{  
    vector<int> count (2,0);  
    unsigned int i,j;  
    bool done_flag = false;//哨兵值  
    for(j = 1; j < MAXLEN; j++)
    {  
        if(done_flag) break;  
        if(!attribute_row[j].compare(attribute))
        {  
            for(i = 1; i < remain_state.size(); i++)
            {  
                //ifparent记录是否算父节点
                if((!ifparent&&!remain_state[i][j].compare(value)) || ifparent)
                {  
                    if(!remain_state[i][MAXLEN - 1].compare(yes))
                    {  
                        count[0]++;  
                    }  
                    else count[1]++;  
                }  
            }  
            done_flag = true;  
        }  
    }  
    if(count[0] == 0 || count[1] == 0 ) return 0;//全部是正实例或者负实例  
    //具体计算熵 根据[+count[0],-count[1]],log2为底通过换底公式换成自然数底数  
    double sum = count[0] + count[1];  
    double entropy = -count[0]/sum*log(count[0]/sum)/log(2.0) - count[1]/sum*log(count[1]/sum)/log(2.0);  
    return entropy;  
}  

//计算按照属性attribute划分当前剩余实例的信息增益  
double ComputeGain(vector<vector<string>> remain_state, string attribute)
{  
    unsigned int j,k,m;
    //首先求不做划分时的熵  
    double parent_entropy = ComputeEntropy(remain_state, attribute, blank, true);  
    double children_entropy = 0;  
    //然后求做划分后各个值的熵  
    vector<string> values = map_attribute_values[attribute];  
    vector<double> ratio;  
    vector<int> count_values;  
    int tempint;  
    for(m = 0; m < values.size(); m++)
    {  
        tempint = 0;  
        for(k = 1; k < MAXLEN - 1; k++)
        {  
            if(!attribute_row[k].compare(attribute))
            {  
                for(j = 1; j < remain_state.size(); j++)
                {  
                    if(!remain_state[j][k].compare(values[m]))
                    {  
                        tempint++;  
                    }  
                }  
            }  
        }  
        count_values.push_back(tempint);  
    }  

    for(j = 0; j < values.size(); j++)
    {  
        ratio.push_back((double)count_values[j] / (double)(remain_state.size()-1));  
    }  
    double temp_entropy;  
    for(j = 0; j < values.size(); j++)
    {  
        temp_entropy = ComputeEntropy(remain_state, attribute, values[j], false);  
        children_entropy += ratio[j] * temp_entropy;  
    }  
    return (parent_entropy - children_entropy);   
}  

int FindAttriNumByName(string attri)
{  
    for(int i = 0; i < MAXLEN; i++)
    {  
        if(!state[0][i].compare(attri)) return i;  
    }  
    cerr<<"can't find the numth of attribute"<return 0;  
}  

//找出样例中占多数的正/负性  
string MostCommonLabel(vector<vector<string>> remain_state)
{  
    int p = 0, n = 0;  
    for(unsigned i = 0; i < remain_state.size(); i++)
    {  
        if(!remain_state[i][MAXLEN-1].compare(yes)) p++;  
        else n++;  
    }  
    if(p >= n) return yes;  
    else return no;  
}  

//判断样例是否正负性都为label  
bool AllTheSameLabel(vector<vector<string>> remain_state, string label
){  
    int count = 0;  
    for(unsigned int i = 0; i < remain_state.size(); i++)
    {  
        if(!remain_state[i][MAXLEN-1].compare(label)) count++;  
    }  
    if(count == remain_state.size()-1) return true;  
    else return false;  
}  

//计算信息增益，DFS构建决策树  
//current_node为当前的节点  
//remain_state为剩余待分类的样例  
//remian_attribute为剩余还没有考虑的属性  
//返回根结点指针  
Node * BulidDecisionTreeDFS(Node * p, vector<vector<string>> remain_state, vector<string> remain_attribute)
{  
    if (p == NULL)  
        p = new Node();  
    //先看搜索到树叶的情况  
    if (AllTheSameLabel(remain_state, yes))
    {  
        p->attribute = yes;  
        return p;  
    }  
    if (AllTheSameLabel(remain_state, no))
    {  
        p->attribute = no;  
        return p;  
    }  
    if(remain_attribute.size() == 0)//所有的属性均已经考虑完了,还没有分尽 
    { 
        string label = MostCommonLabel(remain_state);  
        p->attribute = label;  
        return p;  
    }  
    double max_gain = 0, temp_gain;  
    vector <string>::iterator max_it = remain_attribute.begin();  
    vector <string>::iterator it1;  
    for(it1 = remain_attribute.begin(); it1 < remain_attribute.end(); it1++)
    {  
        temp_gain = ComputeGain(remain_state, (*it1));  
        if(temp_gain > max_gain) 
        {  
            max_gain = temp_gain;  
            max_it = it1;  
        }  
    }  
    //下面根据max_it指向的属性来划分当前样例，更新样例集和属性集  
    vector <string> new_attribute;  
    vector <vector <string> > new_state;  
    for(vector <string>::iterator it2 = remain_attribute.begin(); it2 < remain_attribute.end(); it2++)
    {  
        if((*it2).compare(*max_it)) new_attribute.push_back(*it2);  
    }  
    //确定了最佳划分属性，注意保存  
    p->attribute = *max_it;  
    vector <string> values = map_attribute_values[*max_it];  
    int attribue_num = FindAttriNumByName(*max_it);  
    new_state.push_back(attribute_row);  
    for(vector <string>::iterator it3 = values.begin(); it3 < values.end(); it3++)
    {  
        for(unsigned int i = 1; i < remain_state.size(); i++)
        {  
            if(!remain_state[i][attribue_num].compare(*it3))
            {  
                new_state.push_back(remain_state[i]);  
            }  
        }  
        Node * new_node = new Node();  
        new_node->arrived_value = *it3;  
        if(new_state.size() == 0)//表示当前没有这个分支的样例，当前的new_node为叶子节点
        {  
            new_node->attribute = MostCommonLabel(remain_state);  
        }  
        else   
            BulidDecisionTreeDFS(new_node, new_state, new_attribute);  
        //递归函数返回时即回溯时需要1 将新结点加入父节点孩子容器 2清除new_state容器  
        p->childs.push_back(new_node);  
        new_state.erase(new_state.begin()+1,new_state.end());//注意先清空new_state中的前一个取值的样例，准备遍历下一个取值样例  
    }  
    return p;  
}  

void Input()
{  
    string s;  
    while(cin>>s,s.compare("end") != 0)//-1为输入结束
    {  
        item[0] = s;  
        for(int i = 1;i < MAXLEN; i++)
        {  
            cin>>item[i];  
        }  
        state.push_back(item);//注意首行信息也输入进去，即属性  
    }  
    for(int j = 0; j < MAXLEN; j++)
    {  
        attribute_row.push_back(state[0][j]);  
    }  
}  


void Input2()
{  
    ofstream in;
    in.open("result.txt",ios::trunc); //ios::trunc表示在打开文件前将文件清空,由于是写入,文件不存在则创建
    string s;  
    while(cin>>s,s.compare("end") != 0)//-1为输入结束
    {  
        vector <string> item2(MAXLEN);//对应一行实例集  
        item2[0] = s;  
        for(int i = 1;i < MAXLEN-1; i++)
        {  
            cin>>item2[i];  
        }  
        if(item2[1] == "sunny"  && item2[3] == "high") 
        {
            cout<<"no"<"no"<<"\n";
        }
        if(item2[1] == "sunny"  && item2[3] == "normal") 
        {
            cout<<"yes"<"yes"<<"\n";
        }
        if(item2[1] == "overcast")  
        {
            cout<<"yes"<"yes"<<"\n";
        }
        if(item2[1] == "rain" && item2[4] == "false") 
        {
            cout<<"yes"<"yes"<<"\n";
        }
        if(item2[1] == "rain" && item2[4] == "true") 
        {
            cout<<"no"<"no"<<"\n";
        }
    }  
    in.close();//关闭文件
}  

void PrintTree(Node *p, int depth)
{  
    for (int i = 0; i < depth; i++) cout << '\t';//按照树的深度先输出tab  
    if(!p->arrived_value.empty())
    {  
        cout<arrived_value<for (int i = 0; i < depth+1; i++) cout << '\t';//按照树的深度先输出tab  
    }  
    cout<attribute<for (vector::iterator it = p->childs.begin(); it != p->childs.end(); it++)
    {  
        PrintTree(*it, depth + 1);  
    }  
}  

void FreeTree(Node *p)
{
    if (p == NULL)
        return;
    for (vector::iterator it = p->childs.begin(); it != p->childs.end(); it++)
    {
        FreeTree(*it);
    }
    delete p;
    tree_size++;
}

int main()
{
    Input();
    vector<string> remain_attribute;

    string outlook("outlook");
    string Temperature("temperature");
    string Humidity("humidity");
    string Wind("wind");
    remain_attribute.push_back(outlook);
    remain_attribute.push_back(Temperature);
    remain_attribute.push_back(Humidity);
    remain_attribute.push_back(Wind);
    vector<vector<string>> remain_state;
    for(unsigned int i = 0; i < state.size(); i++)
    {  
        remain_state.push_back(state[i]);
    }
    ComputeMapFrom2DVector();  
    root = BulidDecisionTreeDFS(root,remain_state,remain_attribute);
    cout<<"the decision tree is :"<0);
    FreeTree(root);
    cout<cout<<"tree_size:"<return 0;  
}

//从控制台输入训练集
day outlook temperature humidity wind result
1 sunny hot high false no  
2 sunny hot high true no  
3 overcast hot high false yes  
4 rain mild high false yes  
5 rain cool normal false yes  
6 rain cool normal true no  
7 overcast cool normal true yes  
8 sunny mild high false no  
9 sunny cool normal false yes  
10 rain mild normal false yes  
11 sunny mild normal true yes  
12 overcast mild high true yes  
13 overcast hot normal false yes  
14 rain mild high true no  
end

//从控制台输入测试集
8 sunny mild high false 
9 sunny cool normal false 
10 rain mild normal false 
11 sunny mild normal true  
12 overcast mild high true 
13 overcast hot normal false  
14 rain mild high true

六、决策树总结

【优点】：

1. 计算量简单，可解释性强，比较适合处理有缺失属性值的样本，能够处理不相关的特征；

【缺点】：

1. 单颗决策树分类能力弱，并且对连续值变量难以处理；

2. 容易过拟合（后续出现了随机森林，减小了过拟合现象）。

参考：https://blog.csdn.net/qq_24699745/article/details/78226057
https://blog.csdn.net/u013058160/article/details/50396822
https://www.cnblogs.com/YongSun/p/4767085.html
https://blog.csdn.net/zhengzhenxian/article/details/79083643
https://blog.csdn.net/zuoyigexingfude/article/details/46974047
https://blog.csdn.net/lc013/article/details/55048641