循环神经网络（一般RNN）推导

本文章的例子来自于WILDML

vanillaRNN是相比于LSTMs和GRUs简单的循环神经网络，可以说是最简单的RNN。

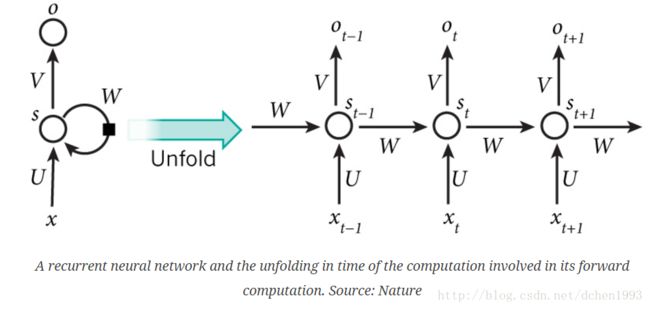
RNN结构

RNN的一个特点是所有的隐层共享参数 (U,V,W) ，整个网络只用这一套参数。

RNN前向传导

st=tanh(Uxt+Wst−1)
ot=softmax(Vst)

st 为 t 时刻隐层的状态值，为向量。
ot 为 t 时刻输出的值（这里是输入一个 xt 就有一个输出 ot ，这个是不必要的，也可以在全部x输入完之后开始输出，根据具体应用来设计模型）

本文例子介绍：RNN语言模型

关于语言模型的介绍就不说了，是NLP基础。这里只说说输入和输出的内容。

语言模型的生成属于无监督学习，只需要大量的文本即可生成。我们只需要做的是构造训练数据。

构造过程：
1. 生成词典vocab。（分词、去掉低频词）
2. 将语料中的句子转为word_id序列，并在头尾加上开始和结束id。
3. 生成训练数据：对于每个句子，输入为前len(sent)-1的序列，输出为后len(sent)-1的序列（也就是输入一个词就预测下一个词）

如，“我 在 沙滩 上 玩耍”输入的向量为 [0,5,85,485,416,55] ，输出的向量为 [5,85,485,416,55,1]

假设我们的词汇有8000个，采用one-hot向量，则每个输入 xt 为8000维，对应的位置为1，其他为0。隐层设置100个神经元。
则列出网络所有参数和输入输出的shape，方便推导：
xt∈R8000
ot∈R8000
st∈R100
U∈R100×8000
V∈R8000×100
W∈R100×100

总参数量为 2HC+H2 ，即1,610,000。

损失函数（loss function）采用交叉熵：
Et(yt,y^t)=−ytlogy^t
E(y,y^)=∑tEt(yt,y^t)=−∑tytlogy^t
其中 yt 为t时刻正确的词语， y^t 为t时刻预测的词语。

反向传播

反向传播目的就是求预测误差 E 关于所有参数 (U,V,W) 的梯度，即 ∂E∂U 、 ∂E∂V 和 ∂E∂W 。

如下图所示，每个时刻t预测的词都有相应的误差，我们需要求这些误差关于参数的所有梯度，最后进行参数的下降调整操作（由于目标是降低Loss function，所以是梯度下降，如果是目标是最大似然，则为梯度上升）。

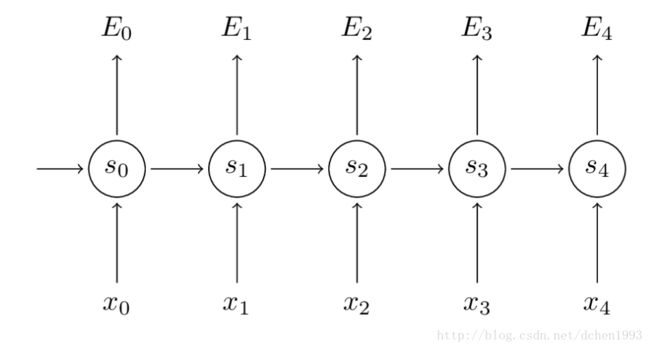
我们这里以计算 E3 关于参数的梯度为例（其他 Et 都需要计算）：

∂E3∂V=∂E3∂y^3∂y^3∂V=∂E3∂y^3∂y^3∂z3∂z3∂V=(y^3−y3)×s3

为8000x100的向量，其中 z3=Vs3 ，用到了softmax的求导公式。

可见关于V的梯度用不到上一层的状态值，所以不需要累计。

BPTT（Backpropagation Through Time）

下面来求解关于W的梯度：
∂E3∂W=∂E3∂y^3∂y^3∂s3∂s3∂W

由于 s3=tanh(Ux3+Ws2) 依赖 s2 ，而 s2 依赖 W 和 s1 ，以此类推。
下图为链式关系：

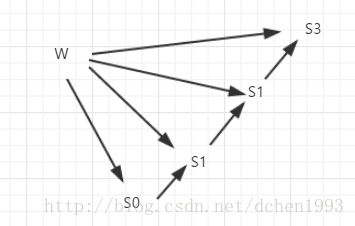
所以，

∂E3∂W=∑k=03∂E3∂y^3∂y^3∂s3∂s3∂sk∂sk∂W

可见由于W在所有隐层中共享，许多变量都依赖W，导致求导链变长，这就是BPTT的特点，将每层的影响都累计起来。

下图为各链接之间的导数，在所有层中不会改变，也体现了传播的路径。

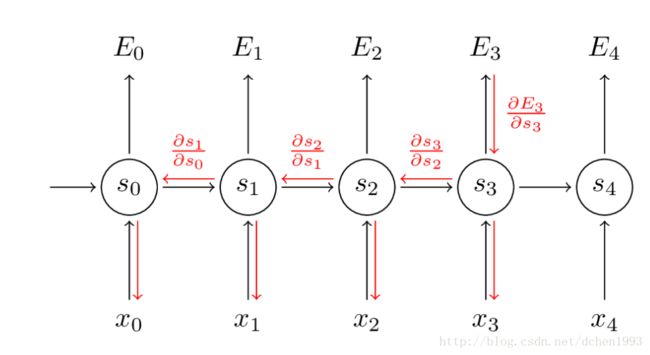
跟一般的反向传播一样，这里也定义一个Delta 向量：
δ(3)2=∂E3∂s3∂s3∂s2∂s2∂z2
其中 z2=Ux2+Ws1 ，在本例子中为一个100x1的向量。

所以 ∂E3∂W 可以写成：

∂E3∂W=∑k=03δ(3)k∂zk∂W

为100x100的矩阵。

同理 ∂E3∂U 可以写成：

∂E3∂U=∑k=03δ(3)k∂zk∂U

为100x8000的矩阵。

至此，关于 (U,V,W) 的梯度都求解完毕。

下面，用代码来解释这个过程会更加清晰明了：

def bptt(self, x, y):
    T = len(y)
    # Perform forward propagation
    o, s = self.forward_propagation(x)
    # We accumulate the gradients in these variables
    dLdU = np.zeros(self.U.shape)
    dLdV = np.zeros(self.V.shape)
    dLdW = np.zeros(self.W.shape)
    delta_o = o
    delta_o[np.arange(len(y)), y] -= 1.
    # For each output backwards...
    for t in np.arange(T)[::-1]:
        dLdV += np.outer(delta_o[t], s[t].T)
        # Initial delta calculation: dL/dz
        delta_t = self.V.T.dot(delta_o[t]) * (1 - (s[t] ** 2))
        # Backpropagation through time (for at most self.bptt_truncate steps)
        for bptt_step in np.arange(max(0, t-self.bptt_truncate), t+1)[::-1]:
            # print "Backpropagation step t=%d bptt step=%d " % (t, bptt_step)
            # Add to gradients at each previous step
            dLdW += np.outer(delta_t, s[bptt_step-1])              
            dLdU[:,x[bptt_step]] += delta_t
            # Update delta for next step dL/dz at t-1
            delta_t = self.W.T.dot(delta_t) * (1 - s[bptt_step-1] ** 2)
    return [dLdU, dLdV, dLdW]

delta_o为 (y−y^)∈RT×8000
从T-1时刻开始计算直到0时刻。

梯度消失问题

tanh函数及其导数的图像：

可见tanh导数的值域是(0,1]，两端都非常平缓并趋于0。
再看我们的梯度公式：

∂E3∂W=∑k=03∂E3∂y^3∂y^3∂s3(∏j=k+13∂sj∂sj−1)∂sk∂W

∂sk∂sk−1 用的就是tanh导数，在训练的后期，梯度会变得比较小，如果几个趋于0的值相乘的话，乘积就会变得非常小，就会出现梯度消失现象。同样的情况也会出现在sigmoid函数。
由于远距离的时刻的梯度贡献接近于0，因此很难学习到远距离的依赖关系。

也很容易想象到当导数都很大的时候，就会出现梯度爆炸的情况，但是它的受重视程度不如梯度消失问题，原因有二：
1. 梯度爆炸很明显，梯度值会变成NaN，程序会崩溃。
2. 用一个预定义值来裁剪梯度值是解决梯度爆炸的一个非常简单实用的办法，而梯度消失问题则很难解决。

幸好还有一些办法来解决梯度消失问题。
1. 合适的参数初始化可以减少梯度消失的影响。
2. 使用ReLU激活函数
3. LSTM和GRU架构。

Reference

http://www.wildml.com/2015/10/recurrent-neural-networks-tutorial-part-3-backpropagation-through-time-and-vanishing-gradients/
http://www.wildml.com/2015/09/recurrent-neural-networks-tutorial-part-2-implementing-a-language-model-rnn-with-python-numpy-and-theano/