Coursera机器学习-第十周-Large Scale Machine Learning

Gradient Descent with Large Datasets

Learning With Large Datasets
我们已经知道，得到一个高效的机器学习系统的最好的方式之一是，用一个低偏差(low bias)的学习算法，然后用很多数据来训练它。 下面是一个区分混淆词组的例子：

但是，大数据存在一个问题，当样本容量m=1,000时还行，但是当m=100,000,000呢？请看一下梯度下降的更新公式：

计算一个 θ 值需要对1亿个数据进行求和，计算量显然太大，所以时间消耗肯定也就大了。
当然，这都是建立在低偏差(low bias)的问题上。如果问题本身不是低偏差，那么m取1,000与100,000,000并无多大区别。
简单回顾一下高偏差(低方差.underfit)，高方差(低偏差)的问题：

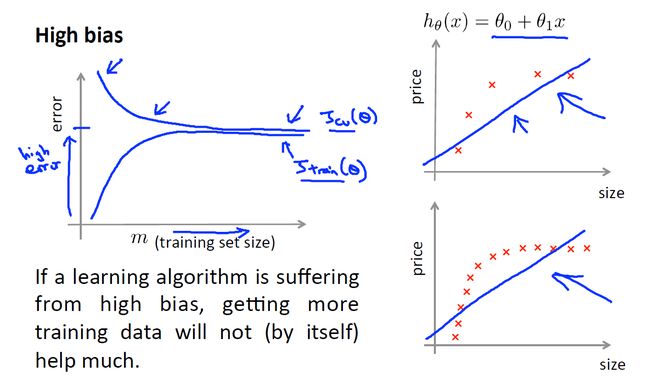我们发现，当学习曲线处于low bias(high variance)状态时，我们可以通过增加样本数量来提高准确度。

Stochastic Gradient Descent
先来看线性回归方程的梯度(有时称batch gradient descent，因为需要计算所有数据)求解:

那么在你运行梯度下降的过程中，多步迭代最终会将参数锁定到全局最小值，迭代的轨迹看起来非常快地收敛到全局最小(上图右侧)，而梯度下降法的问题是当m值很大时，计算这个微分项的计算量就变得很大，因为需要对所有m个训练样本求和。

由此引入Stochastic Gradient Descent(随机梯度下降算法):

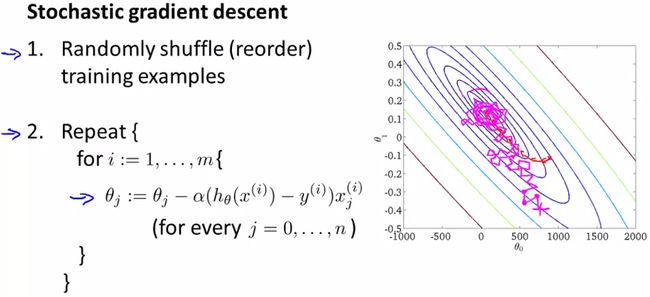
与上述梯度下降算法不同的是，随机梯度下降算法每次 不必关注所有样本，而是对每个样本都进行梯度求解，换句话说，首先对第一组训练样本 x(1),y(1) ，对它的代价函数计算一小步的梯度下降(即将参数 θ 稍微修改一点)，使其对第一个训练样本的拟合变得好一点，然后再转向第二组训练样本，以此类推，直到完成 m 个样本。外部循环会多次遍历整个训练集。
与批量梯度下降算法不同的是，随机梯度算法的下降方向不像批量梯度下降算法那样径直向全局最小值走去，而是以一种比较随机、迂回的路径逼近全局最小值（实际上，随机梯度下降是在某个靠近全局最小值的区域内徘徊，而不是直接逼近全局最小值并停留在那点）。
通常情况下，外层循环会1-10次比较经典。
Mini-Batch Gradient Descent
三种梯度算法比较：

有没有方法兼顾批处理方法，与随机梯度下降方法的优势？就是Mini-batch Gradient Descent。基本思想是：不是批处理的每次处理所有样本，也不是随机方法每次单个样本，而是每次处理b个样本（ 1<b≪m ）

小批量梯度算法：

小批量梯度下降的一个缺点是有一个额外的参数b，你需要调试小批量大小。因此会需要一些时间，但是如果你有一个好的向量化实现这种方法，有时甚至比随机梯度下降更快。

Stochastic Gradient Descent Convergence

• 当你运行这个算法时，你如何确保调试过程已经完成并且能正常收敛呢？

• 怎样调整随机梯度下降中学习速率α的值 ？

  
  确保算法收敛，一个标准的方法是画出最优化的代价函数关于迭代次数的变化
  对于Batch gradient descent而言，因为需要对所有样本进行处理，当样本容量 m 小时，尚且可以处理。但是，当 m 变为很大的时候，方法就行不通了。
  对于Stochastic gradient descent而言，因为只需要处理单个数据样本 x(i),y(i) ，所以计算量上显然比批量梯度下降要少很多。

  当随机梯度下降法对训练集进行扫描时，在我们使用某个样本 (x(i),y(i)) 来更新 θ 前。让我们来计算出这个假设对这个训练样本的表现（在更新 θ 前来完成这一步，原因是如果我们用这个样本更新 θ 以后，再让它在这个训练样本上预测，其表现就比实际上要更好了。
  最后，为了检查随机梯度下降的收敛性， 要做的就是每1000次迭代运算中，对最后1000个样本的cost值求平均然后画出来，通过观察这些画出来的图，我们就能检查出随机梯度下降是否在收敛。
  PS：随机梯度下降算法的第一步就是重新排列样本，所以不存在1000个样本都是一样的情况

以下是几种学习曲线的情况：

上左起第一幅图：
蓝色线已趋于平缓，说明算法已近收敛。 红色线是将学习速率 α 变小之后的学习曲线，似乎变得更好了一些。
上左起第二幅图：
蓝色线已趋于平缓，说明算法已近收敛。 红色线是将取1000的平均值变为取5000，学习曲线变得更为平缓。
下左起第一幅图：
蓝色线不断震荡(并没有明显下降趋势)，似乎算法没有很好地学习。 红色线同样将取的样本平均数变多，可能是由1000变为5000，学习曲线变得稍微平缓，并且有收敛的趋势。
下左起第二幅图：
蓝色线你会发现曲线是实际上是在上升,这是一个很明显的信号，告诉你算法正在发散，那么你要做的就是用一个更小一点的学习速率 α

Stochastic gradient descent:

一般而言，学习速率 α 是一个定值，所以在随机梯度下降算法中，梯度下降的方向总会是迂回的：

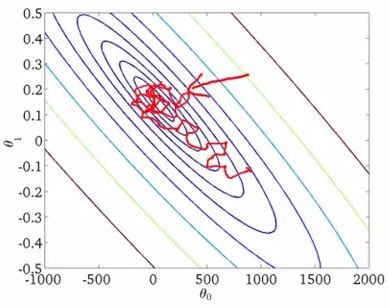
如果将 α 改为一个随时间减少的值，例如：

那么会有助于算法得到全局最小值(注意梯度下降的方向)：

但是，这个需要额外的工作量去确定一些常数值。

Advanced Topics

Online Learning
在线学习机制让我们可以模型化问题，在拥有连续一波数据或连续的数据流涌进来 而我们又需要 一个算法来从中学习的时候来模型化问题。

1. 使用连续的数据流去建立模型
2. 类似随机梯度下降算法，对每个样本进行梯度
3. 自适应个体偏好(例如个体随着时间、经济环境等因素产生的偏好不同问题)

Map Reduce and Data Parallelism
将数据集进行划分，然后发送到每个任务节点，让它们各自执行，然后反馈给一个中央节点，让它对结果进行整合。

示意图：

关于mapreduce的通俗原理请见： http://server.zol.com.cn/329/3295529.html
注：mapreduce是hadoop的一个框架.