K-Means聚类算法

本文系翻译（原文），必要时揉入了自己的理解，各位看官，如有错误还望多多包涵。

1.引言

       前面说过，机器学习是一门处理数据的学科，计算机发展至今，也诞生了数不胜数的跟数据有关的智能算法，正因为这些算法才让那些从事数据分析和处理的人们得以发挥自己的聪明才智。这些算法表面上看似极其复杂无比，但是如果你有心将它们一一整理并且深入的理解，那么在你需要时，你会发现找到一个适合的算法应用到你的工作中并不是一件难事。

       在有关数据挖掘和机器学习的课程中，通常都会以聚类算法为开始来进行讲解，这是因为聚类算法不仅简单而且有用，比如在非监督学习中，聚类就是一个非常重要的部分。在大多数情况下，我们并不能知道有关期望输出的更多信息，我们有的只是一堆数据，并且还要求算法效果尽可能的好，这种情况下，我们往往期望的是，算法能够做到将一堆数据分成几大类，并且每一类中的数据点尽可能的相同，各类间的数据差异性又尽可能的大，也即各类间隔尽可能的远。其中数据点可以表示任何东西，比如某电商的消费客户，如果我们想将这些客户划分成几个不同的消费群体，以便于对不同的群体展开不同的营销活动达到利益最大化，满足了这一需要，我们就可以认为这个聚类算法是有用的。

2.K-Means聚类

       接着，我们来认识下著名的K-Means聚类算法，众所周知，这个算法超级常用，不管在数据挖掘还是在计算机视觉，乃至机器学习中，可以说出镜率极高，当然算法效果也是极佳的。

2.1 准备工作

      首先，需要定义一个距离函数，表示数据点之间的相似度，常用的有欧氏距离、汉明距离等；

      其次，给定需要的聚类数目，即K-Means中的k值；

2.2 基本思想

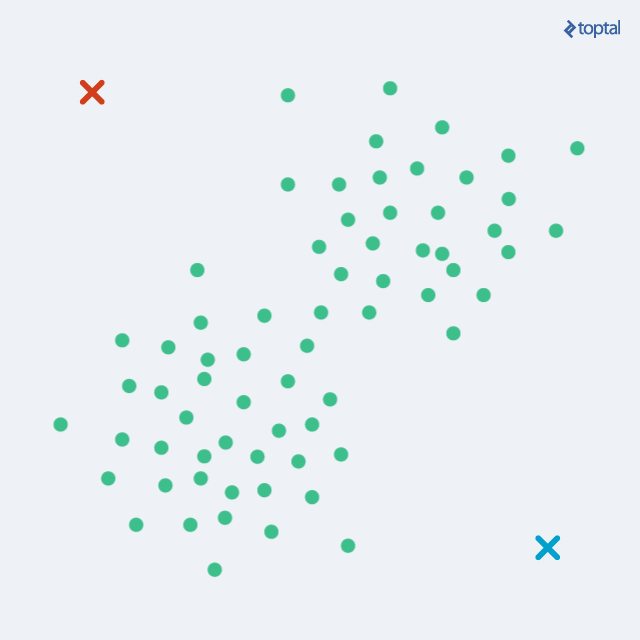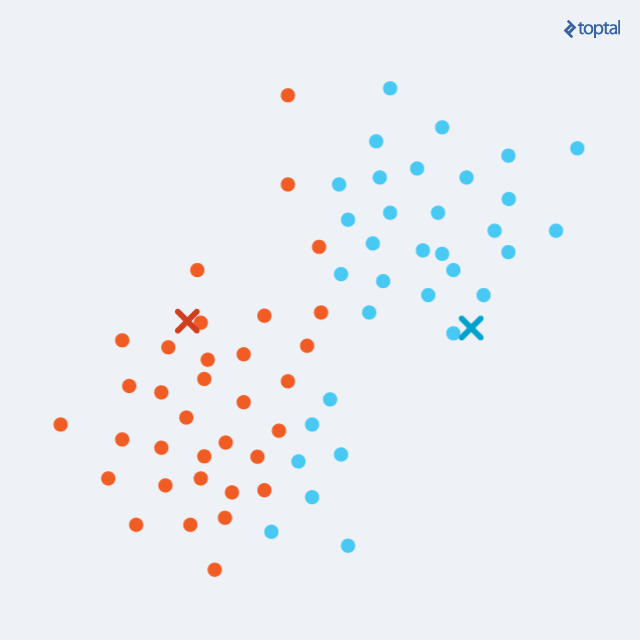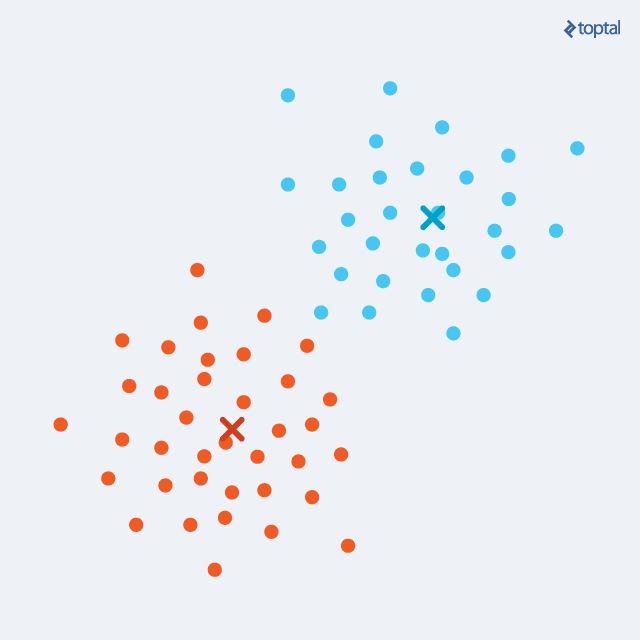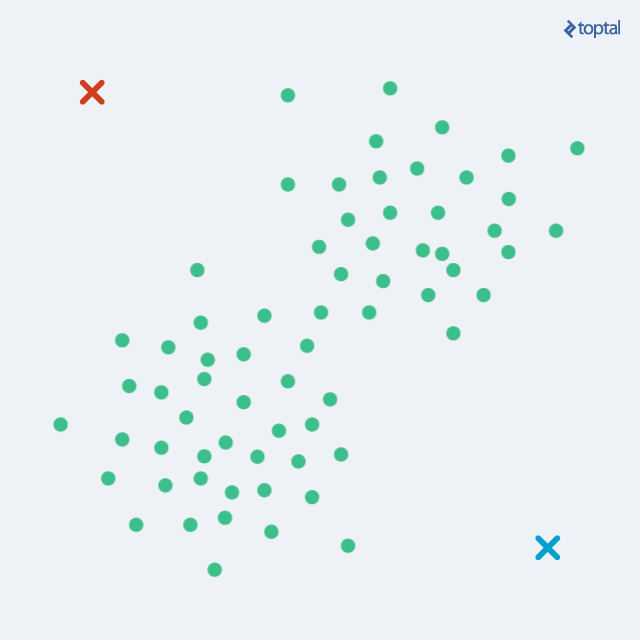
      1）初始化聚类中心：随机化选择k个中心点（聚类的中心或质心（Centroid））作为初始聚类，当然，这个初始化选取除了随机的方式，还可以通过其他方式来选择；

初始化完成后，开始重复下面两个步骤进行迭代：

      2）分配：把数据集中的每一个点都分配到离初始聚类中心或质心（Centroid）最接近的聚类中。具体做法是，对于每一个数据点，分别遍历计算它们到k个聚类中心的距离，然后将其放到距离的最近的那个聚类中，这样就会有k个初始的聚类；

      3）更新：对每一个聚类，分别计算聚类中所有数据点的均值（Means），并将这个均值作为新的聚类的中心或质心（Centroid）；上一步中，我们是将数据分配到一个类，得到每一个聚类，这一步中，对于上述每一个聚类，我们就要计算聚类均值作为聚类新的聚类中心或质心（Centroid）。

      在经过上面每一次迭代后，聚类中心就会慢慢的移动，数据集中每一个数据点到聚类中心的距离也会变得越来越小，如下图；这样通过分配阶段和更新阶段不断交替，就可以最终让算法慢慢收敛，就是指在数据点的分配阶段不会有更大的变化。在有限步迭代后，相同的点集就会被分配到同一个聚类中心，因而分布在同一个聚类，因此K-Means聚类可以保证局部最优，但却不是一个最好的全局解决方案，或者说并非全局最优。

       对于K-Means而言，最终的聚类结果完全依赖于初始聚类中心的选取，对于这一步也有很多不同的解决思路，其中有一个简单的解决法案是，先利用随机的初始化分配方式迭代K-Means有限次，然后把每一个点到其聚类中心距离总和最小的那一次迭代作为最好的聚类结果，也就是说首先我们要想办法使误差最小化。

       另外还有一些其他的选取初始聚类中心的方法，但也都是基于距离的，这种思想尽管可以得到更好的聚类结果，但是却存在一个问题；对于那些远离聚类中心的外点（outliers）来说可能就是某种存在的误差，因为他们距离任何一个现有的聚类中心都很远，这样的话就会导致这些稀少的外点最终自成一类；为了解决这一现象，Arthur 和Vassilvitskii于2007年提出了一种K-Means的改进，叫做K-Means++，这个算法仍然是随机选取初始点，但是基于‘被选中当做初始点的概率与其到聚类中心的距离平方成正比’这一思想来展开；这样一来，那些离得较远的点就会有很高的概率被选中为初始中心点，因此，如果有一组数据点，一个点被选中的概率就会随着他们距离远近的增加而增加，于是解决了上面提到的外点问题。

       另外，K-Means++还是Python机器学习项目Scikit-learn中K-Means的默认初始化方法，如果你用的是Python，那么你就可以使用它，而对于Java，Weka库可能更好。

3.举例

Java（Weka）：

// Load some data
Instances data = DataSource.read("data.arff");

// Create the model
SimpleKMeans kMeans = new SimpleKMeans();

// We want three clusters
kMeans.setNumClusters(3);

// Run K-Means
kMeans.buildClusterer(data);

// Print the centroids
Instances centroids = kMeans.getClusterCentroids();
for (Instance centroid: centroids) {
  System.out.println(centroid);
}

// Print cluster membership for each instance
for (Instance point: data) {
  System.out.println(point + " is in cluster " + kMeans.clusterInstance(point));
}

Python（Scikit-learn）：

>>> from sklearn import cluster, datasets
>>> iris = datasets.load_iris()
>>> X_iris = iris.data
>>> y_iris = iris.target

>>> k_means = cluster.KMeans(n_clusters=3)
>>> k_means.fit(X_iris)
KMeans(copy_x=True, init='k-means++', ...
>>> print(k_means.labels_[::10])
[1 1 1 1 1 0 0 0 0 0 2 2 2 2 2]
>>> print(y_iris[::10])
[0 0 0 0 0 1 1 1 1 1 2 2 2 2 2]

       上面的Python例子中，使用了一个叫“Iris”的数据集，它包含了三种拥有不同花瓣和花萼尺寸的不同种类的鸢尾花，现在我们要把它们分为三类，然后把聚类得到的类与真实类相比较，看看是否匹配。

       这种情况下，我们知道有三种聚类，K-means算法就会非常完美的识别出哪一个属于哪一聚类；但是一般情况下我们应该如何选择一个适合的聚类数量呢？这一类似的问题在机器学习中相当普遍，一般来说，如果我们的聚类数量越多，那么每一个聚类的规模就会越小，因此总的误差（数据点到聚类中心的距离总和 ）也会越小，从上面看来，是不是把K设的越大就越好呢？未必。。假设我们把K值设为我们数据集的样本数M，也就是说，每一个点都有他们自己的聚类中心，每一个聚类也只有一个数据点，这时你会发现它的误差总和为0，但是这又有什么意义呢，我们既不能得到一个对数据更简洁的描述，也不能范化到其它可能出现的新数据点，这种情况就叫做所谓的过拟合（overfitting），并不是我们期望的。

        一种处理这一问题的方法是，对那些拥有较大数量数据点的聚类加入某种惩罚，现在我们不仅要最小化误差，而且要最小化误差和惩罚。误差可能会随着聚类数量的增加而逐渐收敛到0，但是惩罚项却会一直增加，甚至在某些点，增加聚类带来的增益往往小于引进的惩罚项，一个解决办法是使用BIC（Bayesian Information Criterion）贝叶斯信息准则，又叫做X-means，由Pelleg 和Moore于2000年提出。

       还有一个同样重要的问题，有关距离函数的。有时对于直观的目标来说，逻辑函数就够了，而对于空间中的数据点来说，欧式距离是一个明确选择，但是对于不同单位特征，或者离散变量来说欧氏距离就显的有点棘手，这需要大量的专业领域知识，或者可以从机器学习中寻求帮助。我们可以对距离函数进行学习，如果我们有一个带有已知标签的数据点集，就可以利用有监督的学习技术来找到一个适合的函数表达，然后再将这个函数应用到无标签的数据集上。

4.后记

        K-Means中使用用的方法，以及算法迭代中不断交替出现的那两个步骤（分配和更新）一起又组成了一个新的算法：Expectation-MaximizationEM算法，事实上，它只是EM最简单的一种。