深度学习（Deep Learning）读书思考七：循环神经网络二（LSTM）

概述

通过前一节对循环神经网络RNN的了解，简单的RNN虽然能够解决长期依赖问题，但是训练和优化比较困难，然后长短时记忆模型LSTM很大程度上解决长期依赖问题，本文主要介绍

1.LSTM的提出
2.LSTM网络结构
3.LSTM的分析

LSTM的提出

早在94年Hochreiter发现了RNN训练过程中的梯度消失和爆炸问题，然后在99年提出LSTM解决该问题。

梯度消失问题的原因可以参考之前的介绍。

常量错误传播

RNN难训练的主要原因在后向传播过程中，梯度随着时间序列的增加而逐渐消失。如果误差能够不消减的进行传递，则可以避免训练难得问题。

常量错误传播-直观想法

假设隐藏层只有一个节点j，则该节点误差计算过程为

δj(t)=f′j(netj(t))δj(t+1)wjj

其中 netj(t)表示该节点的网络输入,δj(t)表示节点j的误差 .
如果想做到常误差传播，则需要

f′j(netj(t))wjj=1

此时可以近似无限长时间序列，但是网络过于简单并且实现比较复杂。

常量错误木马(Constant Error Carousel-CEC)

LSTM也是根据CEC演化而来。

针对上面的必要条件 f′j(netj(t))wjj=1 ，两边同时积分可以得到

fj(netj(t))=netj(t)wjj

对于任意时序网络输入 netj(t) 都要满足。
此时激活函数必须是线性并且激活值保持为常量。

yj(t+1)=fj(netj(t+1))=fj(wjjyj(t))=yj(t)

此时激活函数必须满足 f(x)=x，并且wjj=1
作者将满足这个等式的传播称之为 CEC。

当然如果满足CEC的约束条件能够进行常误差传播，但是该网络结构过于简单，同时有两个相关问题需要解决：

1.输入权重冲突：隐藏层节点不仅要保存历史信息，还要对当前的输入进行响应。
2.输出权重冲突：同理隐藏层节点不仅保存历史信息，还要响应该节点到输出层的反馈。
因此隐藏层不仅保存历史信息还要对输入和输出进行不同程度的响应，会导致相关的权重更新冲突。这也是LSTM加入门节点的重要原因之一。

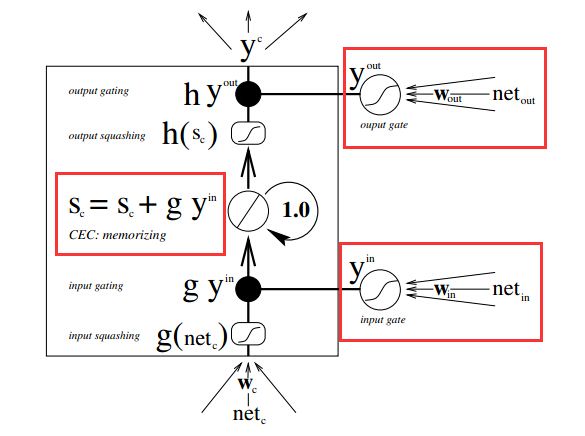
LSTM原型

为了解决1）常量误差传播2）冲突问题，作者通过引入内存单元和门单元重新构建了网络结构。
输入门：能够保护内存单元的内容不受不相关输入的影响，最大程度保存有用信息。
输出门：能够保护其他单元不受不相关内存的影响。网络拓扑如下：

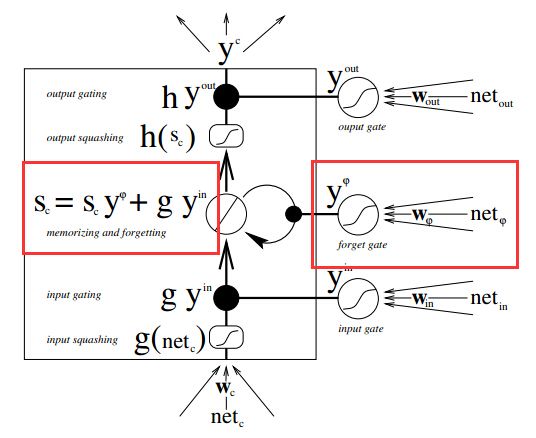
1.y_in表示输入门 ,y_out表示输出门。门在网络结构中相当于新引入隐藏节点，不过激活函数一般选取为sigmoid，将权重压缩到0-1之间
2.内存单元状态 sc 用于存储历史信息和当前输入。
3.内存块，这也是该模型长短时记忆由来的原因。在一个内存块中可以有多个内存单元，他们有着相同的输入和输出门。引入内存块能够减少门的个数，加快计算效率。

引入遗忘门

为了解决状态不断累加问题，引入遗忘门对状态进行缩减。网络结构如下：

引入Peephole Connection

为了学习到更精确的时序，引入Peephole Connection，使得各种门的状态能够学习更准确。这也是目前使用最多的网络结构。

LSTM经典网络结构

目前使用较多的网络结构如下图所示：

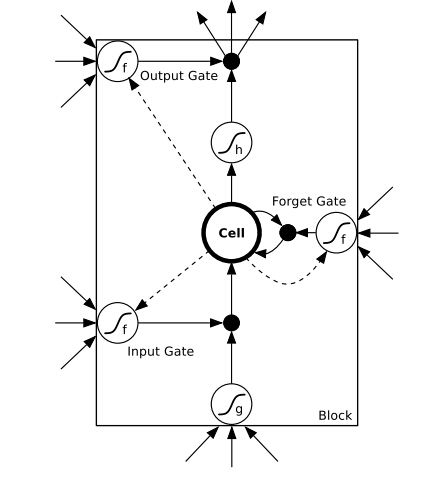
1.上图展示的是一个内存块并且内存块中仅有一个内存单元
2.网络结构中包括输入、输出和遗忘门；Cell为内存状态单元；虚线表示Peephole连接。

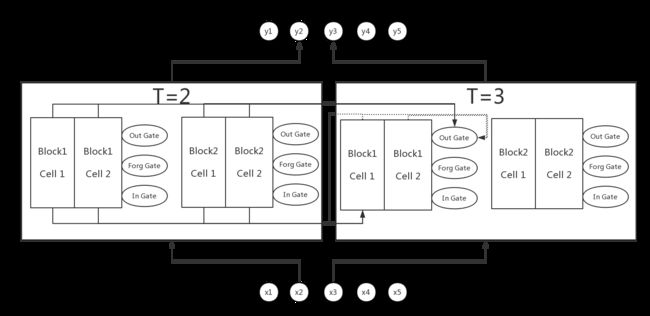
LSTM展开图

下图更形象的展示了LSTM的网络结构，隐藏层有两个内存块，每个内存块有2个单元。

LSTM数学表达

符号定义

I 表示输入集合
H 表示隐藏层节点个数
C为内存块中细胞单元个数
K表示输出层节点个数
γ,ϕ,ω分布表示输入门、遗忘门以及输出门
S表示内存单元状态

前向遍历过程

某个内存块计算过程如下：

1. 输入门表达
   atγbtγ=∑i=1Iwi,γxti+∑h=1Hwh,γbt−1h+∑c=1Cwc,γst−1c=f(atγ)
   输入门的输入依次来自于原始输入x、前一时序隐藏层h、前一时序内存节点状态
2. 遗忘门表达
   atϕbtϕ=∑i=1Iwi,ϕxti+∑h=1Hwh,ϕbt−1h+∑c=1Cwc,ϕst−1c=f(atϕ)
   类似于输入门，遗忘门的输入依次来自于原始输入x、前一时序隐藏层h、前一时序内存节点状态
3. 细胞单元表达
   atcstc=∑i=1Iwi,cxti+∑h=1Hwh,cbt−1h=btϕst−1c+btγg(atc)
   中间状态计算包括两部分一是通过遗忘门加权的前一时序的状态值；二是通过输入门进行加权后的当前单元的输入
4. 输出门表达
   atωbtω=∑i=1Iwi,ωxti+∑h=1Hwh,ωbt−1h+∑c=1Cwc,ωstc=f(atω)
   输出门的输入依次来自于原始输入x、前一时序隐藏层h、当前时序内存节点状态。需要注意的是：输出门控制的是当前细胞单元的输出，因此需要依赖当前节点的状态。
5. 内存单元输出
   btc=btωh(stc)
   内存单元的最终输出可以用于连接输出层和下一时序的隐藏层输入。

后向遍历过程

后向遍历过程，类似于RNN，需要计算得到各个节点的误差，然后传递到相关的权重。

符号定义

ϵtc=∂L∂btc 表示细胞单元输出的误差，即到达 btc 时的汇总误差
ϵts=∂L∂stc 表示中间状态的误差
δtk 表示输出层节点的误差

1.细胞节点误差

ϵtc=∑k=1Kwckδtk+∑g=1Gwcgδt+1g

误差主要来自于1）输出层传递的误差2）下一时序输出门、输入门、遗忘门和中间状态传递的误差，其中G=4H分别表示各个部分
2.输出门误差

δtω=f′(atω)∑c=1Ch(stc)ϵtc

由于一个内存块共享一个输出门，因此需要对该内存块中的各个节点进行误差累加
3.细胞状态误差

ϵtc=btωh′(stc)ϵtc+bt+1ϕϵt+1s+wc,γδt+1γ+wc,ϕδt+1ϕ+wc,ωδtω

误差依次来自于1）细胞输出传递的误差2）后一时序细胞状态的误差3）后一时序输入门的误差4）后一时序遗忘门的误差5）输出门的误差
4.细胞节点的误差

δtc=btγg′(atc)ϵts

5.遗忘门误差

δtϕ=f′(atϕ)∑c=1Cst−1cϵts

6.输入门误差

δtγ=f′(atγ)∑c=1Cg(atc)ϵts

LSTM分析

优势

1.在一个内存块中LSTM能够做到常误差传递（通过后向传递过程可以得到）；以及在不同时序阶段中通过输入门和遗忘门的控制能够使得误差极大化向后传递；最终使得LSTM能够解决较长的依赖问题
2.LSTM能够处理噪声、连续型输入以及分布式表示等问题
3.LSTM泛化能力较其他模型强
4.不需要细粒度参数调优，而且计算复杂度和RNN一致

局限

1.计算复杂度线性增加
2.RNN加上相关优化算法能够解决100以内依赖问题，LSTM能够处理1000以内依赖问题；对于更长的依赖LSTM也会遇到梯度相关问题。

总结

通过本文学习能够非常清楚LSTM的网络结构以及求解算法、理解LSTM内存块内的常量误差传递。