Java:求两个正整数的最大公约数和最小公倍数
求两个正整数的最大公约数和最小公倍数
题目描述:求两个正整数的最大公约数和最小公倍数。
算法设计思路:
1. 辗转相除法求最大公约数:用较小数除较大数,再用出现的余数(第一余数)去除除数,再用出现的余数(第二余数)去除第一余数,如此反复,直到最后余数是0为止。如果是求两个数的最大公约数,那么最后的除数就是这两个数的最大公约数。
2. 等值算法(更相减损法)求最大公约数:
第一步:任意给定两个正整数;判断它们是否都是偶数。若是,则用2约简;若不是则执行第二步。
第二步:以较大的数减较小的数,接着把所得的差与较小的数比较,并以大数减小数。继续这个操作,直到所得的减数和差相等为止。
则第一步中约掉的若干个2与第二步中等数的乘积就是所求的最大公约数。
3. 相减法求最大公约数:
有两整数a和b:
① 若a>b,则a=a-b
② 若a
③ 若a=b,则a(或b)即为两数的最大公约数
④ 若a≠b,则再回去执行①
4. 穷举法求最大公约数:
有两整数a和b:
① i=1
② 若a,b能同时被i整除,则t=i
③ i++
④ 若 i <= a(或b),则再回去执行②
⑤ 若 i > a(或b),则t即为最大公约数,结束。
5. 公式法求最小公倍数:
由于两个数的乘积等于这两个数的最大公约数与最小公倍数的积。即(a,b)×[a,b]=a×b。所以,求两个数的最小公倍数,就可以先求出它们的最大公约数,然后用上述公式求出它们的最小公倍数。
6. 短除法求最小公倍数:
先把每个数的因数找出来,然后再找出公因数,最后在公因数中找出最大公因数。后来,使用分解质因数法来分别分解两个数的因数,再进行运算。之后又演变为短除法。短除法运算方法是先用一个除数除以能被它除尽的一个质数,以此类推,除到商是质数为止。
源代码如下:
package chapter02;
import java.util.Scanner;
import java.util.regex.Matcher;
import java.util.regex.Pattern;
import javax.print.attribute.standard.Sides;
/**
* 求两个正整数的最大公约数和最小公倍数
* @author Jack
* @date 2018-9-5
* @version 1.0
*/
public class GcdAndLCM {
public static void main(String[] args) {
boolean flag = true;
while (flag) {
System.out.println("*****************求最大公约数与最小公倍数*****************");
System.out.println("1:使用辗转相除法求两个正整数的最大公约数");
System.out.println("2:使用等值算法(更相减损法)求两个正整数的最大公约数");
System.out.println("3:使用相减法求两个正整数的最大公约数");
System.out.println("4:使用穷举法求两个正整数的最大公约数");
System.out.println("5:使用公式法求两个正整数的最小公倍数");
System.out.println("6:使用短除法求两个正整数的最小公倍数");
System.out.println("7:使用辗转相除法求三个正整数的最大公约数");
System.out.println("8:使用公式法求三个正整数的最小公倍数");
System.out.println("请选择一种计算方法:(1-8),退出系统请按(N/n)");
Scanner sc = new Scanner(System.in);
boolean isValidate;
switch (sc.next()) {
case "1":
String[] numbers = {};
boolean isValidate1;
boolean isValidate2;
do {
numbers = inputNumber();// 从键盘输入数据
isValidate1 = validate(numbers[0]); // 检测输入数字是否正确
isValidate2 = validate(numbers[1]);
} while (!isValidate1 || !isValidate2);
int result = divisionAlgorithm(new Integer(numbers[0]), new Integer(numbers[1]));
System.out.println(numbers[0] + "和" + numbers[1] + "的最大公约数为:" + result);
break;
case "2":
do {
numbers = inputNumber();
isValidate1 = validate(numbers[0]);
isValidate2 = validate(numbers[1]);
} while (!isValidate1 || !isValidate2);
result = equalAlgorithm(new Integer(numbers[0]), new Integer(numbers[1]));
System.out.println(numbers[0] + "和" + numbers[1] + "的最大公约数为:" + result);
break;
case "3":
do {
numbers = inputNumber();
isValidate1 = validate(numbers[0]);
isValidate2 = validate(numbers[1]);
} while (!isValidate1 || !isValidate2);
result = subtractionAlgorithm(new Integer(numbers[0]), new Integer(numbers[1]));
System.out.println(numbers[0] + "和" + numbers[1] + "的最大公约数为:" + result);
break;
case "4":
do {
numbers = inputNumber();
isValidate1 = validate(numbers[0]);
isValidate2 = validate(numbers[1]);
} while (!isValidate1 || !isValidate2);
result = exhaustAlgorithm(new Integer(numbers[0]), new Integer(numbers[1]));
System.out.println(numbers[0] + "和" + numbers[1] + "的最大公约数为:" + result);
break;
case "5":
do {
numbers = inputNumber();
isValidate1 = validate(numbers[0]);
isValidate2 = validate(numbers[1]);
} while (!isValidate1 || !isValidate2);
result = formulaAlgorithm(new Integer(numbers[0]), new Integer(numbers[1]));
System.out.println(numbers[0] + "和" + numbers[1] + "的最小公倍数为:" + result);
break;
case "6":
do {
numbers = inputNumber();
isValidate1 = validate(numbers[0]);
isValidate2 = validate(numbers[1]);
} while (!isValidate1 || !isValidate2);
result = shortDivisionAlgorithm(new Integer(numbers[0]), new Integer(numbers[1]));
System.out.println(numbers[0] + "和" + numbers[1] + "的最小公倍数为:" + result);
break;
case "7":
do {
numbers = inputNumber();
isValidate1 = validate(numbers[0]);
isValidate2 = validate(numbers[1]);
} while (!isValidate1 || !isValidate2);
System.out.println("请输入第三个正整数:");
Scanner scanner = new Scanner(System.in);
int num3 = scanner.nextInt();
result = threeParametersGcd(new Integer(numbers[0]), new Integer(numbers[1]), num3);
System.out.println(numbers[0] + ", " + numbers[1] + "和" + num3 + "的最大公约数为:" + result);
break;
case "8":
do {
numbers = inputNumber();
isValidate1 = validate(numbers[0]);
isValidate2 = validate(numbers[1]);
} while (!isValidate1 || !isValidate2);
System.out.println("请输入第三个正整数:");
scanner = new Scanner(System.in);
num3 = scanner.nextInt();
result = threeParametersLCM(new Integer(numbers[0]), new Integer(numbers[1]), num3);
System.out.println(numbers[0] + ", " + numbers[1] + "和" + num3 + "的最小公倍数为:" + result);
break;
case "Y":
break;
case "y":
break;
case "N":
flag = false;
sc.close();// 关闭资源
break;
case "n":
flag = false;
sc.close();
break;
default:
break;
}
}
}
/**
* 使用辗转相除法求两个正整数的最大公约数
* @param num1 正整数1
* @param num2 正整数2
* @return 两个正整数的最大公约数
*/
public static int divisionAlgorithm(int num1, int num2) {
// 求两个正整数中最大的数
int max = maxNumber(num1, num2);
int result = 0;
if (max == num1) {
// 较大的数除以较小的数并取余数
int remainder = num1 % num2;
while (remainder != 0) {
num1 = num2;
num2 = remainder;
remainder = num1 % num2;
}
result = num2;
} else if (max == num2) {
int remainder = num2 % num1;
while (remainder != 0) {
num2 = num1;
num1 = remainder;
remainder = num2 % num1;
}
result = num1;
}
return result;
}
/**
* 使用等值算法(更相减损法)求两个正整数的最大公约数
* @param num1 正整数1
* @param num2 正整数2
* @return 两个正整数的最大公约数
*/
public static int equalAlgorithm(int num1, int num2) {
// 计算除了多少次2
int count = 0;
while (num1 % 2 == 0 && num2 % 2 == 0) {
num1 = num1 / 2;
num2 = num2 / 2;
count++;
}
int max = maxNumber(num1, num2);
// 两个数之差
int differ = 0;
if (max == num1) {
while ((differ = num1 - num2) != num2) {
if (differ > num2) {
num1 = differ;
} else {
num1 = num2;
num2 = differ;
}
}
} else {
while ((differ = num2 - num1) != num1) {
if (differ > num1) {
num2 = differ;
} else {
num2 = num1;
num1 = differ;
}
}
}
if (count != 0) {
return 2 * count * differ;
} else {
return differ;
}
}
/**
* 使用相减法求两个正整数的最大公约数
* @param num1 正整数1
* @param num2 正整数2
* @return 两个正整数的最大公约数
*/
public static int subtractionAlgorithm(int num1, int num2) {
while (num1 != num2) {
if (num1 > num2) {
num1 -= num2;
} else {
num2 -= num1;
}
}
return num1;
}
/**
* 使用穷举法求两个正整数的最大公约数
* @param num1 正整数1
* @param num2 正整数2
* @return 两个正整数的最大公约数
*/
public static int exhaustAlgorithm(int num1, int num2) {
int result = 0;
int max = maxNumber(num1, num2);
for (int index = 1; index <= max; index++) {
if (num1 % index == 0 && num2 % index == 0) {
result = index;
}
}
return result;
}
/**
* 使用公式法求两个正整数的最小公倍数
* @param num1 正整数1
* @param num2 正整数2
* @return 两个正整数的最小公倍数
*/
public static int formulaAlgorithm(int num1, int num2) {
// 先求出最大公约数
int gcd = divisionAlgorithm(num1, num2);
return num1 * num2 / gcd;
}
/**
* 使用短除法求两个正整数的最小公倍数
* @param num1 正整数1
* @param num2 正整数2
* @return 两个正整数的最小公倍数
*/
public static int shortDivisionAlgorithm(int num1, int num2) {
int index, max;
int result = 1;
// 循环结束标志
boolean flag;
max = maxNumber(num1, num2);
for (index = 2; index <= max; index++) {
flag = true;
while (flag) {
flag = false;
if (num1 % index == 0) {
num1 = num1 / index;
flag = true;
}
if (num2 % index == 0) {
num2 = num2 / index;
flag = true;
}
if (flag == true)
result *= index;
}
max = maxNumber(num1, num2);
}
return result;
}
/**
* 使用辗转相除法求三个正整数的最大公约数
* @param num1 正整数1
* @param num2 正整数2
* @param num3 正整数3
* @return 三个正整数的最大公约数
*/
public static int threeParametersGcd(int num1, int num2, int num3) {
// 先求两个数的最大公约数
int argument = divisionAlgorithm(num1, num2);
int result = divisionAlgorithm(argument, num3);
return result;
}
/**
* 使用公式法求三个正整数的最小公倍数
* @param num1 正整数1
* @param num2 正整数2
* @param num3 正整数3
* @return 三个正整数的最小公倍数
*/
public static int threeParametersLCM(int num1, int num2, int num3) {
// 先求两个数的最小公倍数
int argument = formulaAlgorithm(num1, num2);
int result = formulaAlgorithm(argument, num3);
return result;
}
/**
* 求两个整数中最大的数
* @param num1 整数1
* @param num2 整数2
* @return 两个整数中最大的数
*/
public static int maxNumber(int num1, int num2) {
if (num1 > num2) {
return num1;
} else {
return num2;
}
}
/**
* 求两个整数中最小的数
* @param num1 整数1
* @param num2 整数2
* @return 两个整数中最小的数
*/
public static int minNumber(int num1, int num2) {
if (num1 < num2) {
return num1;
} else {
return num2;
}
}
/**
* 使用正则表达式检测数据合法性
* @param num 被检测数据
* @return 数据是否合法,true表示合法,false表示非法
*/
public static boolean validate(String num) {
// 使用正则表达式测试输入是否为正整数
Pattern pattern = Pattern.compile("^\\+?[1-9][0-9]*$");
Matcher match = pattern.matcher(num);
if (!match.matches()) {
System.out.println("输入数字有错误,请重新输入!");
return false;
}
return true;
}
/**
* 从键盘输入数据
* @return 返回输入的数据
*/
public static String[] inputNumber() {
String[] numbers = new String[2];
System.out.println("请输入第一个正整数:");
Scanner sc = new Scanner(System.in);
numbers[0] = sc.next();
System.out.println("请输入第二个正整数:");
numbers[1] = sc.next();
return numbers;
}
}
运行界面程序流程图及个人体会
一、程序运行结果展示
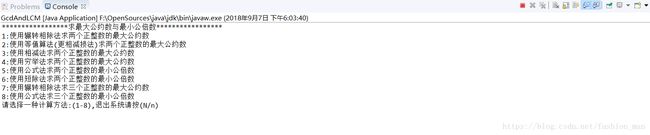
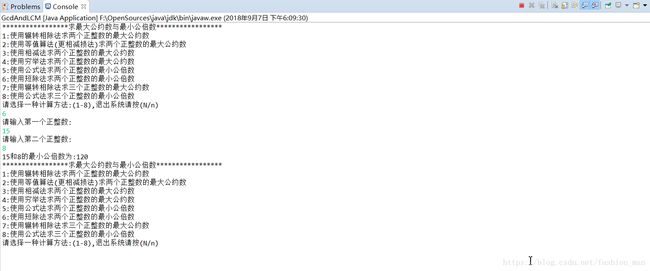
1、初始运行界面如下图:
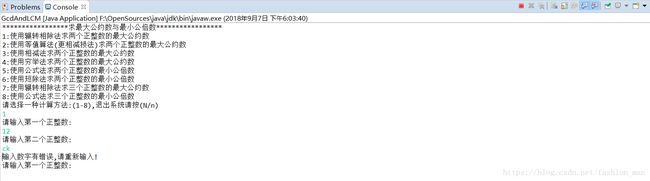
2、输入错误的数据测试运行界面如下图:
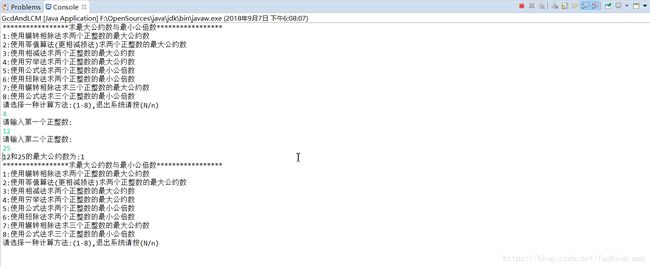
3、输入正确的数据后计算结果及界面如下图:
①辗转相除法求最大公约数:
②等值算法(更相减损法)求最大公约数:
③相减法求最大公约数:
④穷举法求最大公约数:
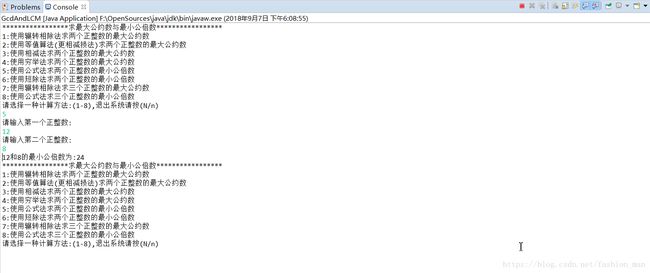
⑤公式法求最小公倍数:
⑥短除法求最小公倍数:
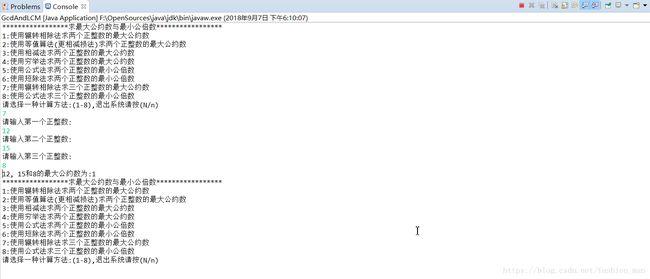
⑦辗转相除法求三个数的最大公约数:
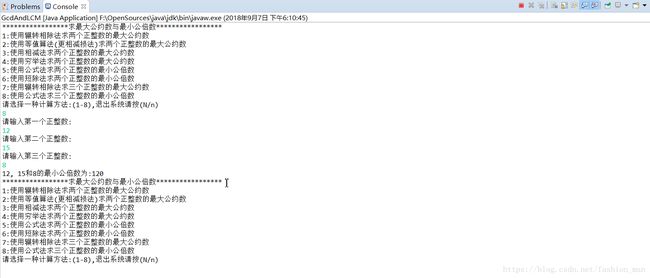
⑧公式法求三个数的最小公倍数:
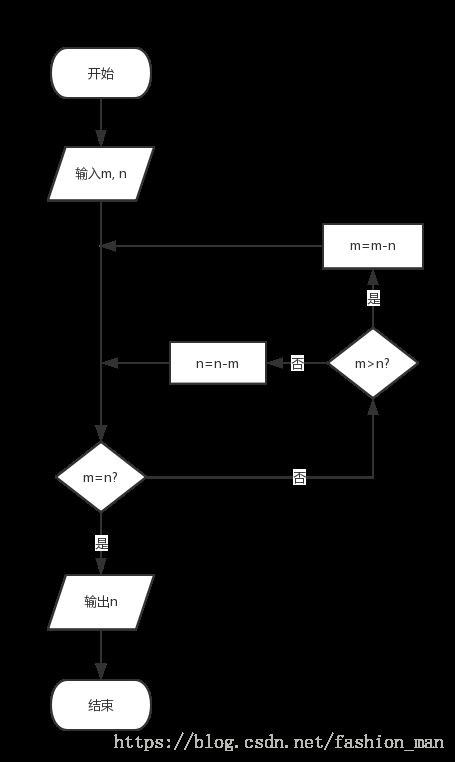
二、程序流程图如下:
①辗转相除法求最大公约数流程图:
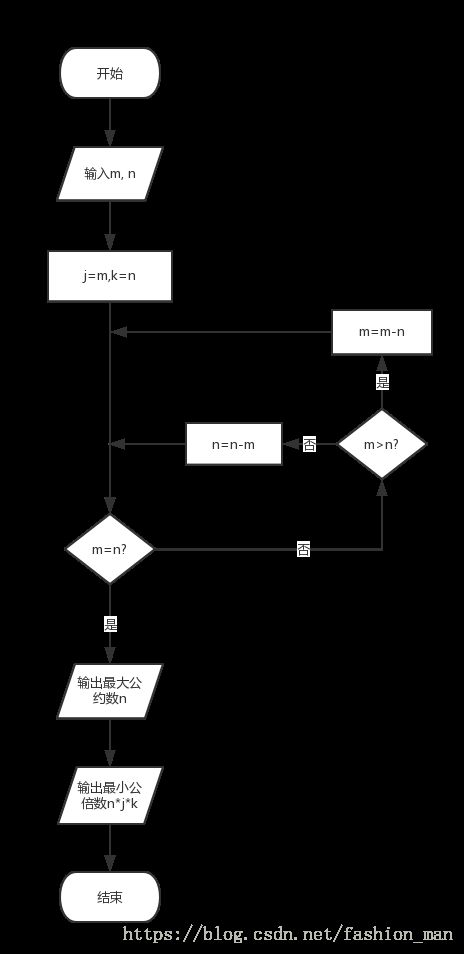
②相减法求最大公约数流程图:
③公式法求最小公倍数流程图:
三、个人总结及心得体会
本次作业是“求两个正整数的最大公约数和最小公倍数”,并能够检测错误数字的输入,以及输入正确的结果。
这次作业的主要问题就在于各种算法的设计上,解决了这一问题,整个程序也就一目了然了,另外我还增加了输入数据正确性的检测功能,如果用户输入的数字不是正整数,会提醒用户重新输入,在这次作业中我分别使用了辗转相除法、相减法、等值法(更相减损法)以及穷举法来求两个正整数的最大公约数,使用公式法和短除法来求两个正整数的最小公倍数,最后终于在不断地检查和修改程序逻辑下,各种算法所得到的结果终于和预期相同。
通过这次作业,我收获到了很多有用的知识,与此同时也发现自己的很多不足之处,基础知识掌握不牢固,程序逻辑总是出错,导致程序调试不成功。在以后的学习中,我会努力提高自己的算法思想和逻辑思维能力,丰富自己的知识面,以便在日后的学习和工作中更好的发挥。
最后,请老师提出建议,在此衷心感谢老师的建议与指导。