机器学习概念篇：监督学习、过拟合，正则化，泛化能力等概念以及防止过拟合方法总结

上个系列【数字图像处理】还将继续更新，最近由于用到机器学习算法，因此将之前学习到的机器学习知识进行总结，打算接下来陆续出一个【机器学习系列】，供查阅使用！本篇便从机器学习基础概念说起！

一、解释监督学习，非监督学习，半监督学习的区别

监督学习、非监督学习和半监督学习区别就是训练数据是否拥有标签信息

1、监督学习：给出了数据及数据的标准答案来训练模型，Regression回归问题、classification分类问题都是典型的监督学习

(1) 监督学习之Regression回归问题举例：房屋价格预测

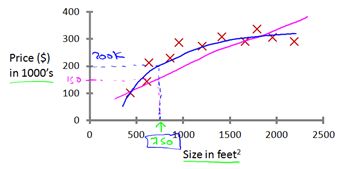
给出了以往房屋面积和价格之间正确实际数据，预测房屋面积和价格之间的关系

(2) 监督学习之classification分类问题

乳腺肿瘤大小和年龄特征判断该肿瘤良性还是恶性，X代表恶性、O代表良性

2、非监督学习：给了一组数据，但没有给出数据的标签(答案)信息，需要我们从数据中去发现数据间隐藏的结构信息，聚类问题是典型的非监督学习。(左：监督，右：非监督学习)

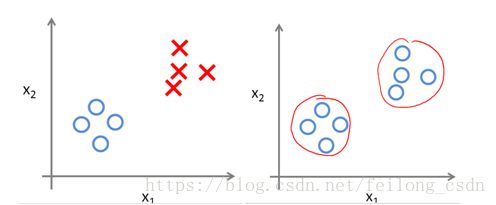
3、半监督学习：给出了大量没有标签的数据和少量拥有标签的数据训练模型

二、解释模型过拟合，欠拟合，正则化，泛化能力

1、欠拟合：模型没有很好的捕捉到数据特征，不能够很好的拟合数据

上左图：没有很好的拟合数据，出现欠拟合；上右图：很好的拟合了数据

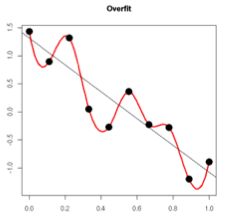
2、过拟合：模型把训练数据学的“太好了”，导致把数据中的潜在的噪声数据也学到了，测试时不能很好的识别数据，模型的泛化能力下降，如下图：

3、正则化：正则化可防止模型过拟合，在训练中数据往往会存在噪声，当我们用模型去拟合带有噪声的数据时，通过假如正则化平衡模型复杂度和损失函数之间的关系，防止模型过拟合，可定义如下公式：

4、范化能力：训练的模型适用于新样本的能力，称为“泛化”能力，具有强范化能力的模型能很好的适用于整个样本空间

三、防止过拟合的处理方法

1、Early Stopping提前终止

Early Stopping既是在训练集迭代收敛之前停止迭代以防止过拟合，看下图：

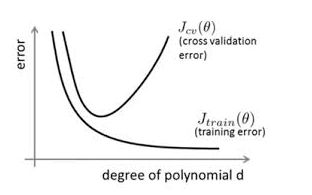
开始随着训练集迭代验证集上的误差随着训练集的误差一起下降，但当迭代超过一定步数之后，训练集的误差还在降低，但是验证集的误差已经不在下降并且误差有所上升，因此当验证集的误差不再变化时，我们便可以提前终止训练

具体做法是：每迭代一定步数之后，我们便计算一些验证集上的存在的误差，当验证集的误差不再降低时，便停止训练。

2、数据集扩增

可以说数据集扩增是防止过拟合最好最根源的方式，有时候拥有更多的数据胜过一个好的模型，过拟合既是在模型训练时对训练数据学习的太好了，举个例子如果我们训练一个东西是不是叶子，如果数据集的叶子都是锯齿状，当模型过拟合时便会认为所有的叶子都是锯齿状的，此时模型再好也不如往数据集中增强新的非锯齿状的叶子，便会防止出现过拟合。
如何获取更多的数据：
(1) 从数据源头获取更多的数据
(2) 根据当前数据集估计数据分布参数，使用该分部产生更多的数据
(3) 数据增强，通过一定规则在现有数据集的基础上扩充数据

3、正则化

正则化思想：由于模型过拟合很大可能是因为训练模型过于复杂，因此在训练时，在对损失函数进行最小化的同时，我们要限定模型参数的数量，即加入正则项，即不是以为的去减小损失函数，同时还考虑模型的复杂程度

未加入正则项的模型损失函数：

加入正则项L后损失函数：

其中λ是正则项系数，是用来权衡正则项和损失函数之间权重，正则化有以下两种：

(1) L1正则化(L1范数)：权重向量w的绝对值之和

(2) L2正则化(L2范数)：权重向量w的平方和再求平方根，欧几里得范数，其中w代表模型的参数，k则代表了模型参数的个数

(3) L1正则化和L2正则化的区别

L1正则化和L2正则化都会使得权重矩阵变小，即权重w变小，因此都具有防止过拟合的能力，但不同是L1正则化更易产生系数的权重矩阵，即权重w变小为0；L2正则化只会是w变小但不会出现大量为0现象

这里请注意，以下给出三个重要解释

解释1：为什么权重w变小能防止过拟合？ 先看下图：

过拟合时，拟合函数的系数往往比较大，正如上图，红色过拟合函数曲线需要估计到训练集中的每一个点，最终形成了波动很大的拟合函数。所以在过拟合函数的某些区间里，函数值的波动很大， 这便会使得函数在该区间的导数值的绝对值很大，由于自变量有大有小，所有只有系数w足够大才能保证导数值足够大。因此控制参数w的范数不要太大，曲线波动便会小，能更好的拟合数据。

解释2：为何L1正则化更易产生系数权重矩阵，而L2不会出现大量w值为0？

先看L1正则化损失函数：

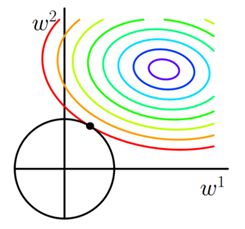
其中J₀是原始损失函数，如下图是在二维空间中，只有两个权重即w1和w2，此时求解J₀可以画出等值线，同时L=∑_w|w| 可以画出方形，当两个图形相交时便得出最优解：

如图所示，当前最优解是：

可以看出L1正则化是权重的绝对值之和，图形有很多突出的角，二维情况下有四个，多维情况下将会更多，J₀与这些角的接触几率远大于与L1其他部分接触的几率，因此最优解中将会有大量是与这些角接触得到的，所以有w = 0，因此L1正则化便会产生稀疏的权重矩阵

我们再来看看L2损失函数：

如下图所示，与L1正则化不同的是L2正则化中L2= α∑_ww² 图形是一个圆，这样最优解w出现为0的几率便会小很多，所以不具有产生稀疏权重矩阵的性质

解释三：为什么假如L2正则化和L1正则化会出现权重衰减？

对L2正则化损失函数 J=J₀+ α∑_ww² 求导得：

可以得出w更新公式为：

在不使用L2正则化时，求导结果中w前的系数为1，先上式w前系数是(1-2ηα)，其中η、α都是整数，因此(1-2ηα)小于1，便会使得w权重衰减：

同理对L1正则化损失函数 J= J₀ + α∑_w|w| 求导可得：

上式sgn表示权重w的符号，因为原式中是绝对值|w|，求导后便有符号，w的更新规则为：

比未加入L1正则化多出了- ηα*sgn(w)，可以分析无论w为正还是为负，在上式中w的绝对值均会变小，出现权重衰减。

4、dropout

dropout是深度学习中降低过拟合风险的方法，神经网络产生过拟合主要是因为神经元之间的协同作用产生的，dropout便是在神经网络训练过程中让部分神经元失活，阻断部分神经元之间的协同作用，减少神经元之间的联合适应性。看下图：

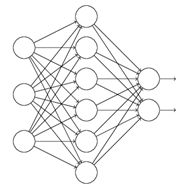
对上图神经网络使用dropout方法后：

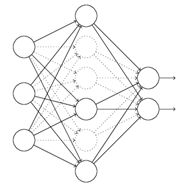
欢迎指正讨论！