优化InnoDB主键
原文:
https://www.percona.com/blog/2018/07/26/tuning-innodb-primary-keys/
The choice of good InnoDB primary keys is a critical performance tuning decision. This post will guide you through the steps of choosing the best primary key depending on your workload.
选择好的InnoDB主键,是性能调优的关键决策。本文将引导你根据你的工作量,选择最佳主键的步骤
As a principal architect at Percona, one of my main duties is to tune customer databases. There are many aspects related to performance tuning which make the job complex and very interesting. In this post, I want to discuss one of the most important one: the choice of good InnoDB primary keys. You would be surprised how many times I had to explain the importance of primary keys and how many debates I had around the topic as often people have preconceived ideas that translate into doing things a certain way without further thinking.
作为Percona的首席架构师,我的一个重要职责就是为客户调优数据库。有许多性能调优方面的事情使得工作变的复杂且有趣。在这篇文章中,我想聊聊最重要的一个问题:选择好的InnoDB主键。你会诧异地发现,我不得不多次解释主键的重要性,以及围绕这个主题做了多少次辩论,因为人们通常会有先入为主的想法,这些想法会转换为以某种方式做事,而没有更进一步的思考
The choice of a good primary key for an InnoDB table is extremely important and can have huge performance impacts. When you start working with a customer using an overloaded x1.16xlarge RDS instance, with close to 1TB of RAM, and after putting a new primary in place they end up doing very well with a r4.4xlarge instance — it’s a huge impact. Of course, it is not a silver bullet –, you need to have a workload like the ones I’ll highlight in the following sections. Keep in mind that tuning comes with trade-offs, especially with the primary key. What you gain somewhere, you have to pay for, performance-wise, elsewhere. You need to calculate what is best for your workload.
对于InnoDB表,选择一个好的主键极其重要,可能会产生巨大的性能影响。当你开始为一个使用x1.16xlarge规格的RDS的客户工作时,使用将近1TB的内存,并将其放至在一个新的主要部分之后,他们最终在r4.4xlarge规格的实例上表现得很好——这是一个巨大影响。当然,这不是一个银色子弹,你需要有一个像我将在以下部分中高亮的工作量,请记住,调优需要权衡,特别是使用主键。你从某个地方得到了什么,同时也需要为其他地方付出性能代价。你需要计算出什么是你最佳的负载
What is special about InnoDB primary keys?
InnoDB主键有何特殊之处?
InnoDB is called an index-organized storage engine. An index-organized storage engine uses the B-Tree of the primary key to stores the data, the table rows. That means a primary key is mandatory with InnoDB. If there is no primary key for a table, InnoDB adds a hidden auto-incremented 6 bytes counter to the table and use that hidden counter as the primary key. There are some issues with the InnoDB hidden primary key. You should always define explicit primary keys on your tables. In summary, you access all InnoDB rows by the primary key values.
InnoDB被称作索引组织引擎。一个索引组织引擎用主键的B树结构存储数据,即表行。这意味着InnoDB强制使用主键。如果一张表没有显式主键,InnoDB添加一个隐式自增的6字节计数器,并使用该隐藏的计数器作为主键。但InnoDB隐式主键存在一些问题。你应该总是在你的表上定义一个显式主键。简言之,你可以通过主键值访问所有的InnoDB行。
An InnoDB secondary index is also a B-Tree. The search key is made of the index columns and the values stored are the primary keys of matching rows. A search by a secondary index very often results in an implicit search by primary key. You can find more information about InnoDB file format in the documentation. Jeremy Cole’s InnoDB Ruby tools are also a great way to learn about InnoDB internals.
一个InnoDB二级索引也是一个B树。搜索键由索引列组成,而且值存储的值是匹配行的主键。通过二级索引的搜索,通常会引起主键的隐式搜索。你可以在文档中找到有关InnoDB文件格式的更多信息。Jeremy Cole的InnoDB Ruby工具也是学习InnoDB内部的好方法。
What is a B-Tree?
什么是B-Tree?
A B-Tree is a data structure optimized for operations on block devices. Block devices, or disks, have a rather important data access latency, especially spinning disks. Retrieving a single byte at a random position doesn’t take much less time than retrieving a bigger piece of data like a 8KB or 16KB object. That’s the fundamental argument for B-Trees. InnoDB uses pieces of data — pages — of 16KB.
B树是针对块设备上经过优化的数据结构,块设备或磁盘具有相当重的访问延迟,尤其是转盘式磁盘。在随机位置检索单个字节并不比检索更大一点的数据(如8KB或16KB的对象)耗时更少。这是B树的基本论点,InnoDb使用16KB的数据页。
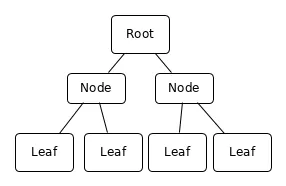
一个简单的三级B树
Let’s attempt a simplified description of a B-Tree. A B-Tree is a data structure organized around a key. The key is used to search the data inside the B-Tree. A B-Tree normally has multiple levels. The data is stored only in the bottom-most level, the leaves. The pages of the other levels, the nodes, only contains keys and pointers to pages in the next lower level.
让我们来简化B树的描述。B树是围绕键所组织的数据结构,键用于搜索B树内部的数据。一个B树通常有多级,数据仅存储在最底层,即叶子。其他级别的页(节点)仅包含下一级别的页的键和指针。
When you want to access a piece of data for a given value of the key, you start from the top node, the root node, compare the keys it contains with the search value and finds the page to access at the next level. The process is repeated until you reach the last level, the leaves. In theory, you need one disk read operation per level of the B-Tree. In practice there is always a memory cache and the nodes, since they are less numerous and accessed often, are easy to cache.
如果要访问键给定值的一段数据,则从顶级节点,即根节点开始,将其包含的键与搜索值进行比较,并找到要在下一级访问的页。这个过程将重复直到你导到最后一级,即叶子。理论上,每级B树需要一次磁盘读操作。在实际中,总是有一个内存缓存和节点,因为他们数量较少且经常访问,易于缓存。
An ordered insert example
一个有序插入示例
Let’s consider the following sysbench table:
我们看一下这个sysbench表
mysql> show create table sbtest1\G
*************************** 1. row ***************************
Table: sbtest1
Create Table: CREATE TABLE `sbtest1` (
`id` int(11) NOT NULL AUTO_INCREMENT,
`k` int(11) NOT NULL DEFAULT '0',
`c` char(120) NOT NULL DEFAULT '',
`pad` char(60) NOT NULL DEFAULT '',
PRIMARY KEY (`id`),
KEY `k_1` (`k`)
) ENGINE=InnoDB AUTO_INCREMENT=3000001 DEFAULT CHARSET=latin1
1 row in set (0.00 sec)
mysql> show table status like 'sbtest1'\G
*************************** 1. row ***************************
Name: sbtest1
Engine: InnoDB
Version: 10
Row_format: Dynamic
Rows: 2882954
Avg_row_length: 234
Data_length: 675282944
Max_data_length: 0
Index_length: 47775744
Data_free: 3145728
Auto_increment: 3000001
Create_time: 2018-07-13 18:27:09
Update_time: NULL
Check_time: NULL
Collation: latin1_swedish_ci
Checksum: NULL
Create_options:
Comment:
1 row in set (0.00 sec)
The primary key B-Tree size is Data_length. There is one secondary key B-Tree, the k_1 index, and its size is given by Index_length. The sysbench table was inserted in order of the primary key since the id column is auto-incremented. When you insert in order of the primary key, InnoDB fills its pages with up to 15KB of data (out of 16KB), even when innodb_fill_factor is set to 100. That allows for some row expansion by updates after the initial insert before a page needs to be split. There are also some headers and footers in the pages. If a page is too full and cannot accommodate an update adding more data, the page is split into two. Similarly, if two neighbor pages are less than 50% full, InnoDB will merge them. Here is, for example, a sysbench table inserted in id order:
主键B树索引大小写在了Data_length,还有一个二级B树索引,即k_1,其大小由Index_length给出。这个sysbench表是按主键顺序插入的,原因是id列是自增的。当你按主键的顺序,有序插入时,即使是innodb_fill_factor设置为100,InnoDB也会最多只用15KB的数据填充其页(out of 16KB?)。这允许在初始插入之后,通过更新进行一些行扩展,然后才需要拆分页。页中还有一些页眉页脚,如果页太满,而且无法容纳更新进来的更多数据,则将页拆分成两个。同样,如果两个相邻页填充率低于50%,InnoDB将合并他们。例如,这是以id有序插入的sysbench表:
mysql> select count(*), TABLE_NAME,INDEX_NAME, avg(NUMBER_RECORDS), avg(DATA_SIZE) from information_schema.INNODB_BUFFER_PAGE
-> WHERE TABLE_NAME='`sbtest`.`sbtest1`' group by TABLE_NAME,INDEX_NAME order by count(*) desc;
+----------+--------------------+------------+---------------------+----------------+
| count(*) | TABLE_NAME | INDEX_NAME | avg(NUMBER_RECORDS) | avg(DATA_SIZE) |
+----------+--------------------+------------+---------------------+----------------+
| 13643 | `sbtest`.`sbtest1` | PRIMARY | 75.0709 | 15035.8929 |
| 44 | `sbtest`.`sbtest1` | k_1 | 1150.3864 | 15182.0227 |
+----------+--------------------+------------+---------------------+----------------+
2 rows in set (0.09 sec)
mysql> select PAGE_NUMBER,NUMBER_RECORDS,DATA_SIZE,INDEX_NAME,TABLE_NAME from information_schema.INNODB_BUFFER_PAGE
-> WHERE TABLE_NAME='`sbtest`.`sbtest1`' order by PAGE_NUMBER limit 1;
+-------------+----------------+-----------+------------+--------------------+
| PAGE_NUMBER | NUMBER_RECORDS | DATA_SIZE | INDEX_NAME | TABLE_NAME |
+-------------+----------------+-----------+------------+--------------------+
| 3 | 35 | 455 | PRIMARY | `sbtest`.`sbtest1` |
+-------------+----------------+-----------+------------+--------------------+
1 row in set (0.04 sec)
mysql> select PAGE_NUMBER,NUMBER_RECORDS,DATA_SIZE,INDEX_NAME,TABLE_NAME from information_schema.INNODB_BUFFER_PAGE
-> WHERE TABLE_NAME='`sbtest`.`sbtest1`' order by NUMBER_RECORDS desc limit 3;
+-------------+----------------+-----------+------------+--------------------+
| PAGE_NUMBER | NUMBER_RECORDS | DATA_SIZE | INDEX_NAME | TABLE_NAME |
+-------------+----------------+-----------+------------+--------------------+
| 39 | 1203 | 15639 | PRIMARY | `sbtest`.`sbtest1` |
| 61 | 1203 | 15639 | PRIMARY | `sbtest`.`sbtest1` |
| 37 | 1203 | 15639 | PRIMARY | `sbtest`.`sbtest1` |
+-------------+----------------+-----------+------------+--------------------+
3 rows in set (0.03 sec)
The table doesn’t fit in the buffer pool, but the queries give us good insights. The pages of the primary key B-Tree have on average 75 records and store a bit less than 15KB of data. The index k_1 is inserted in random order by sysbench. Why is the filling factor so good? It’s simply because sysbench creates the index after the rows have been inserted and InnoDB uses a sort file to create it.
这个表不适合缓冲池,但是查询给了我们好的见解。主键B树的页,平均有75条记录,并存储少于15KB的数据。索引k_1由sysbench以随机顺序插入。为什么填充的如此之好?这是因为sysbench插入行之后创建索引,且InnoDB使用排序文件来创建它
You can easily estimate the number of levels in an InnoDB B-Tree. The above table needs about 40k leaf pages (3M/75). Each node page holds about 1200 pointers when the primary key is a four bytes integer. The level above the leaves thus has approximately 35 pages and then, on top of the B-Tree is the root node (PAGE_NUMBER = 3). We have a total of three levels.
你可以轻松估算InnoDB的B树结构中的级数。上面的表大概需要40k叶子页(3M/75)。当主键为四个字节整数时,每个节点页维持大约1200个指针。因此叶子上级大约有35页,然后B树之上为根节点(PAGE_NUMBER=3)。我们总共有三级
A randomly inserted example
一个随机插入示例
If you are a keen observer, you realized a direct consequence of inserting in random order of the primary key. The pages are often split, and on average the filling factor is only around 65-75%. You can easily see the filling factor from the information schema. I modified sysbench to insert in random order of id and created a table, also with 3M rows. The resulting table is much larger:
如果你是个犀利的观察者,你将意识到以主键随机插入的直接后果。页通常是分开的,平均填充为65-75%左右。你可以轻易通过information_schema查看填充系数。我修改sysbench让id以随机顺序插入到创建好的表,也有3M行。结果表格要大挺多:
mysql> show table status like 'sbtest1'\G
*************************** 1. row ***************************
Name: sbtest1
Engine: InnoDB
Version: 10
Row_format: Dynamic
Rows: 3137367
Avg_row_length: 346
Data_length: 1088405504
Max_data_length: 0
Index_length: 47775744
Data_free: 15728640
Auto_increment: NULL
Create_time: 2018-07-19 19:10:36
Update_time: 2018-07-19 19:09:01
Check_time: NULL
Collation: latin1_swedish_ci
Checksum: NULL
Create_options:
Comment:
1 row in set (0.00 sec)
While the size of the primary key b-tree inserted in order of id is 644MB, the size, inserted in random order, is about 1GB, 60% larger. Obviously, we have a lower page filling factor:
id有序地插入到主键B树中大小为644MB,而id以随机顺序插入则将近1G,大了60%。显然,我们的页填充系数较低。
mysql> select count(*), TABLE_NAME,INDEX_NAME, avg(NUMBER_RECORDS), avg(DATA_SIZE) from information_schema.INNODB_BUFFER_PAGE
-> WHERE TABLE_NAME='`sbtestrandom`.`sbtest1`'group by TABLE_NAME,INDEX_NAME order by count(*) desc;
+----------+--------------------------+------------+---------------------+----------------+
| count(*) | TABLE_NAME | INDEX_NAME | avg(NUMBER_RECORDS) | avg(DATA_SIZE) |
+----------+--------------------------+------------+---------------------+----------------+
| 4022 | `sbtestrandom`.`sbtest1` | PRIMARY | 66.4441 | 10901.5962 |
| 2499 | `sbtestrandom`.`sbtest1` | k_1 | 1201.5702 | 15624.4146 |
+----------+--------------------------+------------+---------------------+----------------+
2 rows in set (0.06 sec)
The primary key pages are now filled with only about 10KB of data (~66%). It is a normal and expected consequence of inserting rows in random order. We’ll see that for some workloads, it is bad. For some others, it is a small price to pay.
主键页现在只填充了10KB的数据(~66%)。这是一个以随机顺序插入行的正常预期结果。我们可以看到,对于某些工作量而言,这很糟糕,对于其他情况而言,这则是一个很小的代价。
A practical analogy
一个实战类比
It is always good to have a concrete model or analogy in your mind to better understand what is going on. Let’s assume you have been tasked to write the names and arrival time, on paper, of all the attendees arriving at a large event like Percona Live. So, you sit at a table close to the entry with a good pen and a pile of sheets of paper. As people arrive, you write their names and arrival time, one after the other. When a sheet is full, after about 40 names, you move it aside and start writing to a new one. That’s fast and effective. You handle a sheet only once, and when it is full, you don’t touch it anymore. The analogy is easy, a sheet of paper represents an InnoDB page.
在你的意识中,有一个具体的模型或者类比总是好的,以便更好地理解正在发生的事情。让我们假设一下你的任务是需要写下,参加Percona Live等大型活动的与会者姓名和到达时间。所以,你坐在靠近入口处的桌子上,拿着一支好笔和一塌纸,当大家到达时,你记录下他们的名字和到达时间,在大约40个名字被记录下之后,表格纸满了,你将它移走并开始写新的一张表格纸,这是最快且有效的。你只需处理一次该表格纸,当它被写满,你不会再接触它。类比很简单,一张表格纸代表InnoDB页。
The above use case represents an ordered insert. It is very efficient for the writes. Your only issue is with the organizer of the event: she keeps coming to you asking if “Mr. X” or “Mrs. Y” has arrived. You have to scan through your sheets to find the name. That’s the drawback of ordered inserts, reads can be more expensive. Not all reads are expensive, some can be very cheap. For example: “Who were the first ten people to get in?” is super easy. You’ll want an ordered insert strategy when the critical aspects of the application are the rate and the latency of the inserts. That usually means the reads are not user-facing. They are coming from report batch jobs, and as long as these jobs complete in a reasonable time, you don’t really care.
上述用例代表一次有序插入,它对写操作特别有效。你唯一的问题是与活动组织者沟通:她一直在问你“X先生”或者“Y太太”是否已经到了。你必须扫描表格纸才能找到姓名,这是有序插入的缺点,读取可能更加昂贵。但并非所有读取都很昂贵,某些情况可能非常轻量,比如:“前十个进入的是谁?”则超级简单。当应用的关键在于插入的速率和延迟时,你将需要一个有序插入的策略。这通常意味着读操作不是面向用户的,它们来自于报告批处理作业,只要这些作业在合理的时间内完成,你就无需过于关注。
Now, let’s consider a random insertion analogy. For the next day of the event, tired of the organizer questions, you decide on a new strategy: you’ll write the names grouped by the first letter of the last name. Your goal is to ease the searches by name. So you take 26 sheets, and on top of each one, you write a different letter. As the first visitors arrive, you quickly realize you are now spending a lot more time looking for the right sheet in the stack and putting it back at the right place once you added a name to it.
现在,我们来聊聊随机插入的类比,比如活动的第二天,厌倦了组织者的问题,你决定了一个新的策略:你以姓氏的第一个字母为分组规则写下名字。你的目的是通过姓名简化搜索。所以你需要26张表格纸,在每张纸上写下一个不同的字母。当第一批参会者到达时,你很快意识到你现在需要花费多少时间在堆栈中寻找到正确的表格纸张,并在为其添加名字之后将它放回正确的位置。
At the end of the morning, you have worked much more. You also have more sheets than the previous day since for some letters there are few names while for others you needed more than a sheet. Finding names is much easier though. The main drawback of random insertion order is the overhead to manage the database pages when adding entries. The database will read and write from/to disk much more and the dataset size is larger.
在早上结束时,你已工作了很多。你仍还有比前一天更多的表格纸张,因为有些字母的姓名非常少,而对于其他字母,你需要的不仅仅是一张表格纸。寻找名字要容易得多。随机顺序插入主要的缺点是,在新增时,管理数据库页带来的开销。数据库从磁盘中大量的读写使得数据集大小更大。
Determine your workload type
确定你的负载场景
The first step is to determine what kind of workload you have. When you have an insert-intensive workload, very likely, the top queries are inserts on some large tables and the database heavily writes to disk. If you repeatedly execute “show processlist;” in the MySQL client, you see these inserts very often. That’s typical of applications logging a lot of data. There are many data collectors and they all wait to insert data. If they wait for too long, some data may be lost. If you have strict SLA on the insert time and relaxed ones on the read time, you clearly have an insert oriented workload and you should insert rows in order of the primary key.
第一个步骤,就是确定你拥有的负载类型。当你有一个插入密集型负载场景时,很可能最频繁的查询是在一些大表上插入的,并且数据库会大量写入硬盘。在MySQL客户端中重复执行"show processlist;",则会经常看到这些插入。这是典型的应用正在记录大量数据,有许多数据采集器,它们都在等待插入数据,如果它们等待时间过长,一些数据可能被丢失。如果你在插入时间上有严格的SLA,而在读取上有较随意的SLA,那么显然你有一个面向插入的负载场景,并且你应该按住键顺序插入。
You may also have a decent insert rate on large tables but these inserts are queued and executed by batch processes. Nobody is really waiting for these inserts to complete and the server can easily keep up with the number of inserts. What matters for your application is the large number of read queries going to the large tables, not the inserts. You already went through query tuning and even though you have good indexes, the database is reading from disk at a very high rate.
你也可以在大表上有着不错的插入效率,但这些插入是按批处理排队并执行的。没有人在真的等待这些插入的完成,并且服务器可以轻松跟上插入的数量。对于你的应用而言,重要的是大量读查询正在进入你的大表,而不是插入。你已经完成了查询优化,即便你已经有良好的索引,但是数据库仍然会以非常高的速率从磁盘中读取数据。
When you look at the MySQL processlist, you see many times the same select query forms on the large tables. The only options seem to be adding more memory to lower the disk reads, but the tables are growing fast and you can’t add memory forever. We’ll discuss the read-intensive workload in details in the next section.
当你查看MySQL的processlist时,你会看到在同一张大表上查询的大量相同语句。这似乎只能增加更多内存来降低磁盘读,但是表增长地很快,你却不能一直增加内存。我们将在下一个话题里详细讨论读密集型负载场景。
If you couldn’t figure if you have an insert-heavy or read-heavy workload, maybe you just don’t have a big workload. In such a case, the default would be to use ordered inserts, and the best way to achieve this with MySQL is through an auto-increment integer primary key. That’s the default behavior of many ORMs.
如果你不能确定你是否有大量插入或者频繁读的负载,那么你可能并没有大的负载。在这种情况下,默认使用有序插入,且使用MySQL实现此方式的最佳方式是通过自增整形主键。这是大多ORM的默认行为。
A read-intensive workload
读密集型负载场景
I have seen quite a few read-intensive workloads over my consulting years, mostly with online games and social networking applications. On top of that, some games have social networking features like watching the scores of your friends as they progress through the game. Before we go further, we first need to confirm the reads are inefficient. When reads are inefficient, the top select query forms will the accessing a number of distinct InnoDB pages close to the number of rows examined. The Percona Server for MySQL slow log, when the verbosity level includes “InnoDB”, exposes both quantities, and the pt-query-digest tool includes stats on them. Here’s an example output (I’ve removed some lines):
还在我做咨询的时代,我就见过很多读密集型场景。主要是在线游戏和社交网络应用。他们中最典型的是,有些游戏还包括了社交网络特性,比如在你朋友游戏的过程中,查看他们的分数。在我们进一步讨论之前,我们先要确认读取效率低。当读取效率低下时,顶部的查询表单将访问许多不同的InnoDB页,这些页数接近检查的行数。Percona Server for MySQL的慢日志,当日志详细级别包含了“InnoDB”时,显示有关它的几个指标,且pt-query-digest工具包含了对它们的统计,这是一个例子的输出(我删除了一些行)
# Query 1: 2.62 QPS, 0.00x concurrency, ID 0x019AC6AF303E539E758259537C5258A2 at byte 19976
# This item is included in the report because it matches --limit.
# Scores: V/M = 0.00
# Time range: 2018-07-19T20:28:02 to 2018-07-19T20:28:23
# Attribute pct total min max avg 95% stddev median
# ============ === ======= ======= ======= ======= ======= ======= =======
# Count 48 55
# Exec time 76 93ms 637us 3ms 2ms 2ms 458us 2ms
# Lock time 100 10ms 72us 297us 182us 247us 47us 176us
# Rows sent 100 1.34k 16 36 25.04 31.70 4.22 24.84
# Rows examine 100 1.34k 16 36 25.04 31.70 4.22 24.84
# Rows affecte 0 0 0 0 0 0 0 0
# InnoDB:
# IO r bytes 0 0 0 0 0 0 0 0
# IO r ops 0 0 0 0 0 0 0 0
# IO r wait 0 0 0 0 0 0 0 0
# pages distin 100 1.36k 18 35 25.31 31.70 3.70 24.84
# EXPLAIN /*!50100 PARTITIONS*/
select * from friends where user_id = 1234\G
The friends table definition is:
friends表定义为:
CREATE TABLE `friends` (
`id` int(10) unsigned NOT NULL AUTO_INCREMENT,
`user_id` int(10) unsigned NOT NULL,
`friend_user_id` int(10) unsigned NOT NULL,
`created` timestamp NOT NULL DEFAULT CURRENT_TIMESTAMP,
`active` tinyint(4) NOT NULL DEFAULT '1',
PRIMARY KEY (`id`),
UNIQUE KEY `uk_user_id_friend` (`user_id`,`friend_user_id`),
KEY `idx_friend` (`friend_user_id`)
) ENGINE=InnoDB AUTO_INCREMENT=144002 DEFAULT CHARSET=latin1
I built this simple example on my test server. The table easily fits in memory, so there are no disk reads. What matters here is the relation between “page distin” and “Rows examine”. As you can see, the ratio is close to 1. It means that InnoDB rarely gets more than one row per page it accesses. For a given user_id value, the matching rows are scattered all over the primary key b-tree. We can confirm this by looking at the output of the sample query:
我在我的测试服务器上,构建了这个简单的例子。该表很适合内存,因此可避免磁盘读。这里重要的是,页面区别和行检查之间的关系。如你所见:该比例接近为1,这意味着InnoDB很少每页访问一行。对于给定的user_id值,匹配的行分散在主键B树上。我们可以通过查看示例查询输出来确认这一点:
mysql> select * from friends where user_id = 1234 order by id limit 10;
+-------+---------+----------------+---------------------+--------+
| id | user_id | friend_user_id | created | active |
+-------+---------+----------------+---------------------+--------+
| 257 | 1234 | 43 | 2018-07-19 20:14:47 | 1 |
| 7400 | 1234 | 1503 | 2018-07-19 20:14:49 | 1 |
| 13361 | 1234 | 814 | 2018-07-19 20:15:46 | 1 |
| 13793 | 1234 | 668 | 2018-07-19 20:15:47 | 1 |
| 14486 | 1234 | 1588 | 2018-07-19 20:15:47 | 1 |
| 30752 | 1234 | 1938 | 2018-07-19 20:16:27 | 1 |
| 31502 | 1234 | 733 | 2018-07-19 20:16:28 | 1 |
| 32987 | 1234 | 1907 | 2018-07-19 20:16:29 | 1 |
| 35867 | 1234 | 1068 | 2018-07-19 20:16:30 | 1 |
| 41471 | 1234 | 751 | 2018-07-19 20:16:32 | 1 |
+-------+---------+----------------+---------------------+--------+
10 rows in set (0.00 sec)
The rows are often apart by thousands of id values. Although the rows are small, about 30 bytes, an InnoDB page doesn’t contain more than 500 rows. As the application becomes popular, there are more and more users and the table size grows like the square of the number of users. As soon as the table outgrows the InnoDB the buffer pool, MySQL starts to read from disk. Worse case, with nothing cached, we need one read IOP per friend. If the rate of these selects is 300/s and on average, every user has 100 friends, MySQL needs to access up to 30000 pages per second. Clearly, this doesn’t scale for long.
行通常相隔数千个id值,尽管行很小,大约30字节,但InnoDB页不超过500行。随着应用变得流行,用户越来越多,表大小也随着用户呈平方数增长。一旦表超过InnoDB缓冲池,MySQL就开始从磁盘中读取。更糟的是,没有缓存,我们每个朋友都需要一次读IOPS。如果这些查询平均速率是300/s,每个用户有100个朋友,则MySQL需要每秒访问30000个页,显然这无法长期扩展。
We need to determine all the ways the table is accessed. For that, I use pt-query-digest and I raise the limit on the number of query forms returned. Let’s assume I found:
-
93% of the times by user_id
-
5% of the times by friend_id
-
2% of the times by id
我们需要决定访问表的所有方式。为此,我使用pt-query-digest并且加大了查询表单的返回数量限制,让我们假设发现:
-
93%的查询量通过user_id
-
5%的查询量通过friend_id
-
2%的查询量通过id
The above proportions are quite common. When there is a dominant access pattern, we can do something. The friends table is a typical example of a many-to-many table. With InnoDB, we should define such tables as:
上述比例非常常见。When there is a dominant access pattern, we can do something。该friends表是多对多表的典型示例。使用InnoDB,我们应将这些表定义为:
CREATE TABLE `friends` (
`id` int(10) unsigned NOT NULL AUTO_INCREMENT,
`user_id` int(10) unsigned NOT NULL,
`friend_user_id` int(10) unsigned NOT NULL,
`created` timestamp NOT NULL DEFAULT CURRENT_TIMESTAMP,
`active` tinyint(4) NOT NULL DEFAULT '1',
PRIMARY KEY (`user_id`,`friend_user_id`),
KEY `idx_friend` (`friend_user_id`),
KEY `idx_id` (`id`)
) ENGINE=InnoDB AUTO_INCREMENT=144002 DEFAULT CHARSET=latin1
Now, the rows are ordered, grouped, by user_id inside the primary key B-Tree but the inserts are in random order. Said otherwise, we slowed down the inserts to the benefit of the select statements on the table. To insert a row, InnoDB potentially needs one disk read to get the page where the new row is going and one disk write to save it back to the disk. Remember in the previous analogy, we needed to take one sheet from the stack, add a name and put it back in place. We also made the table bigger, the InnoDB pages are not as full and the secondary indexes are bigger since the primary key is larger. We also added a secondary index. Now we have less data in the InnoDB buffer pool.
现在,这些行在主键b树内由user_id排序,分组,但插入会按随机的顺序。换句话说,我们放慢了insert速度,使在表上的select语句受益。为了插入一行,InnoDB可能需要一个磁盘读来获取新行所在页和一个磁盘写,以将其保存回磁盘。记住之前的一个类比,我们需要从堆栈中取出一张纸,记下一个名字并将它放回原位。我们还会使得表变得更大,同时InnoDB页填充不够饱满,二级索引更大,因为主键更大。我们还添加了二级索引,现在我们InnoDB缓冲池中的数据更少了。
Shall we panic because there is less data in the buffer pool? No, because now when InnoDB reads a page from disk, instead of getting only a single matching row, it gets up to hundreds of matching rows. The amount of read IOPS is no longer correlated to the number of friends times the rate of select statements. It is now only a factor of the incoming rate of select statements. The impacts of not having enough memory to cache all the table are much reduced. As long as the storage can perform more read IOPS than the rate of select statements, all is fine. With the modified table, the relevant lines of the pt-query-digest output are now:
我们会因为缓冲池中的数据变少而感到恐慌吗?不,因为现在当InnoDB从磁盘中读一个页时,它不会只获得一个匹配的行,取而代之的是拿到数百个匹配的行。读IOPS的数量不再与朋友的数量与select语句的发送数据相关联。没有足够内存来缓存所有表的影响大大被减少了。只要存储比可处理select语句速率更多的读IOPS,一切就挺好。通过修改表,pt-query-digest输出的相关行现在是:
# Attribute pct total min max avg 95% stddev median
# ============ === ======= ======= ======= ======= ======= ======= =======
# Rows examine 100 1.23k 16 34 23.72 30.19 4.19 22.53
# pages distin 100 111 2 5 2.09 1.96 0.44 1.96
With the new primary key, instead of 30k read IOPS, MySQL needs to perform only about 588 read IOPS (~300*1.96). It is a workload much easier to handle. The inserts are more expensive but if their rate is 100/s, it just means 100 read IOPS and 100 write IOPS in the worse case.
有了新主键,而不是30k读IOPS,MySQL只需要处理大概588读IOPS(约300*1.96)。这是一个更容易处理的工作量。插入更加昂贵,但它们的速率如果是100/s,则意味着在最坏情况下,有100读IOPS和100写IOPS。
The above strategy works well when there is a clear access pattern. On top of my mind, here are a few other examples where there are usually dominant access patterns:
-
Game leaderboards (by user)
-
User preferences (by user)
-
Messaging application (by from or to)
-
User object store (by user)
-
Likes on items (by item)
-
Comments on items (by item)
在能够明确访问模式的时候,上述策略很有效。在我脑海中,这里有一些其他的例子,通常是主要的访问模式:
-
游戏排行榜(按用户)
-
用户偏好(按用户)
-
消息传递(从哪到哪)
-
用户对象存储(按用户)
-
我的收藏(按项目)
-
对项目的评论(按项目)
What can you do when you don’t have a dominant access pattern? One option is the use of a covering index. The covering index needs to cover all the required columns. The order of the columns is also important, as the first must be the grouping value. Another option is to use partitions to create an easy to cache hot spot in the dataset. I’ll discuss these strategies in future posts, as this one is long enough!
What can you do when you don’t have a dominant access pattern? 一种选择是使用覆盖索引。覆盖索引需要覆盖所有必要的列,列的顺序也很重要,因为第一个必须是分组值。另一个选择是使用分区,在数据集中创建易于缓存的热点。我将在以后的博文中讨论这个点,因为这个话题有点长。
We have seen in this post a common strategy used to solve read-intensive workload. This strategy doesn’t work all the time — you must access the data through a common pattern. But when it works, and you choose good InnoDB primary keys, you are the hero of the day!
我们在本文中看到了用于解决读密集型负载场景,但是该策略不是始终有用——你必须通过通用模式访问数据。但是在它工作时,你选择好了好的InnoDB主键,你就是这时的英雄!