Tarjan算法
【简介】
Tarjan算法是一种由Robert Tarjan提出的求解有向图强连通分量的线性时间的算法。
【基本思想】
百度Tarjan
一些定义:如果两个顶点可以相互通达,则称两个顶点强连通(strongly connected)。如果有向图G的每两个顶点都强连通,称G是一个强连通图。有向图的极大强连通子图,称为强连通分量(strongly connected components)。
例如,下图中,子图 {1 , 2 , 3 , 4 } 为一个强连通分量,因为顶点 1 , 2 , 3 , 4 两两可达。{ 5 } , { 6 } 也分别是两个强连通分量。
定理:在任何深度优先搜索中,同一强连通分量内的所有顶点均在同一棵深度优先搜索树中(证明去找百度啦)。
Tarjan算法是基于对图深度优先搜索的算法,每个强连通分量为搜索树中的一棵子树。搜索时,把当前搜索树中未处理的节点加入一个栈,回溯时可以判断栈顶到栈中的节点是否为一个强连通分量。
我们定义定义dfn(x)为节点 x 搜索的次序编号(时间戳),low(x)为 x 或 x 的子树能够追溯到的最早的栈中节点的次序号。
当dfn(x)= low(x)时,以 x 为根的搜索子树上所有节点是一个强连通分量。
我们考虑如何更新 x 的 low 值:
- 当点 p 与点 p’ 相连时,如果此时 p’ 不在栈中,p 的 low 值为两点的 low 值中较小的一个。
- 当点 p 与点 p’ 相连时,如果此时 p’ 在栈中,p 的 low 值为 p 的 low 值和 p’ 的 dfn 值中较小的一个。
这些东西本蒟蒻也并不知道该怎么证明,大家可以自行百度
我们以上面的图为例,看一下Tarjan算法的流程:
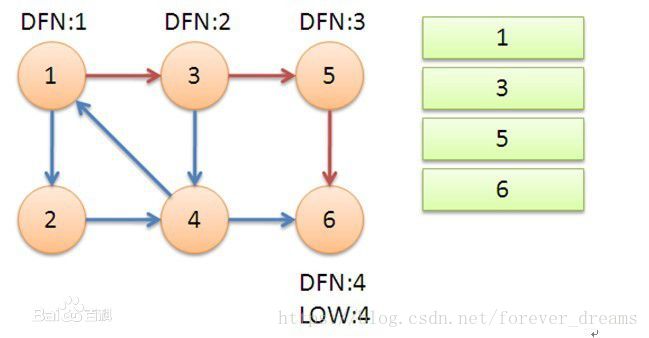
1、从节点1开始DFS,把遍历到的节点加入栈中。搜索到节点 x = 6 时,dfn[ 6 ] = low[ 6 ],找到了一个强连通分量。退栈,{ 6 }为一个强连通分量。
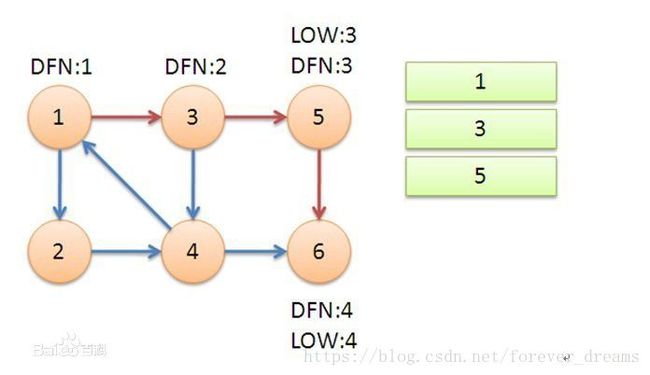
2、返回节点5,发现dfn[ 5 ] = low[ 5 ],退栈后{ 5 }为一个强连通分量。
3、返回节点3,继续搜索到节点4,把4加入栈。发现节点4向节点1有后向边,节点1还在栈中,所以LOW[4]=1。节点6已经出栈,(4,6)是横叉边,返回3,(3,4)为树枝边,所以 low[ 3 ] = low[ 4 ] = 1。
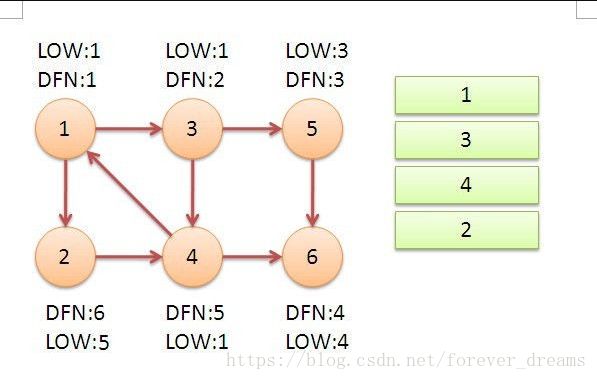
4、继续回到节点1,最后访问节点2。访问边(2,4),4还在栈中,所以 low[ 2 ] = dfn[ 4 ] = 5。返回1后,发现 dfn[ 1 ] = low[ 1 ],把栈中节点全部取出,组成一个强联通分量{ 1 , 3 , 4 , 2 }。
Tarjan搜索时的代码:
void Tarjan(int x)
{
int i,j;
sign++;
low[x]=sign;
dfn[x]=sign;
top++;
sta[top]=x;
insta[x]=true;
for(i=first[x];i;i=next[i])
{
j=v[i];
if(!dfn[j])
{
Tarjan(j);
low[x]=min(low[x],low[j]);
}
else if(insta[j])
low[x]=min(low[x],dfn[j]);
}
if(dfn[x]==low[x])
{
sum++;
do
{
i=sta[top];
id[i]=sum;
num[sum]++;
insta[i]=false;
top--;
}
while(i!=x);
}
}在Tarjan算法中,将强联通分量求出来后再对强联通分量整体进行操作就可以解决问题了
【复杂度分析】
在Tarjan算法中,每个点被访问了一次,每条边被访问了一次,因此时间复杂度为O(m+n)
【例题】
题目传送门受欢迎的牛
这道题就是用个Tarjan然后随便搞一下就行了
#include
#include
#include
using namespace std;
const int N=10005,M=50005;
int n,m,t,sum,top,sign;
int first[N],v[M],next[M];
int du[N],id[N],dfn[N],low[N],num[N],sta[N];
bool insta[N];
void add(int x,int y)
{
t++;
next[t]=first[x];
first[x]=t;
v[t]=y;
}
void Tarjan(int x)
{
int i,j;
sign++;
low[x]=sign;
dfn[x]=sign;
top++;
sta[top]=x;
insta[x]=true;
for(i=first[x];i;i=next[i])
{
j=v[i];
if(!dfn[j])
{
Tarjan(j);
low[x]=min(low[x],low[j]);
}
else if(insta[j])
low[x]=min(low[x],dfn[j]);
}
if(dfn[x]==low[x])
{
sum++;
do
{
i=sta[top];
id[i]=sum;
num[sum]++;
insta[i]=false;
top--;
}
while(i!=x);
}
}
int main()
{
int n,m,i,j,x,y,ans;
bool flag=true;
scanf("%d%d",&n,&m);
for(i=1;i<=m;++i)
{
scanf("%d%d",&x,&y);
add(x,y);
}
for(i=1;i<=n;++i)
if(!dfn[i])
Tarjan(i);
for(i=1;i<=n;++i)
for(j=first[i];j;j=next[j])
if(id[i]!=id[v[j]])
du[id[i]]++;
for(i=1;i<=sum;++i)
{
if(!du[i])
{
if(!flag)
{
printf("0");
return 0;
}
ans=num[i];
flag=false;
}
}
printf("%d",ans);
return 0;
}