【机器学习笔记27】CART算法-回归树和分类树
【参考资料】
【1】《统计学习方法》5.5 CART算法
【2】http://scikit-learn.org/stable/modules/generated/sklearn.tree.DecisionTreeRegressor.html
基本概念
分类和回归树(classification and regression tree, CART) 是应用广泛的决策树学习方法,由特征选择、树的生成和剪枝组成,既可以用做分类也可以用作回归。
回归树
回归树的定义
假设X和Y分别作为输入和输出变量,那么存在训练集
D = { ( x 1 , y 1 ) , ( x 2 , y 2 ) . . . ( x N , y N ) } D = \{(x_1, y_1), (x_2, y_2) ... (x_N, y_N) \} D={(x1,y1),(x2,y2)...(xN,yN)}
一个回归树对应其输入空间(特征)的划分和这个划分上的输入值。 数学定义:
存在M个分类,每个分类的单元为 R M R_M RM,且该单元的输出为 c M c_M cM,我们有回归树模型 f ( x ) = ∑ m = 1 M c M I ( x ∈ R M ) f(x)=\sum\limits_{m=1}^{M}c_MI(x \in R_M) f(x)=m=1∑McMI(x∈RM) ,这里 I I I代表那个分类的集合。
于是我们可以用平方误差 ∑ ( y i − f ( x i ) ) 2 \sum(y_i - f(x_i))^2 ∑(yi−f(xi))2来表示回归树训练时的误差。
回归树的生成
第一步: 选择切分变量j和切分点s,即选用特征j和特征上的一个阈值s将输入数据划分成一个二叉决策树。这一步需要遍历所有的特征及其阈值,获取最优解,数学表示如下:
1)目标是取两个集合: R 1 ( j , s ) = { x ∣ x ( j ) < s } R 2 ( j , s ) = { x ∣ x j > s } R_1(j,s)=\{x|x^{(j)}<s\} \quad R_2(j,s)=\{x|x^{j}>s\} R1(j,s)={x∣x(j)<s}R2(j,s)={x∣xj>s}
2)求解误差最小值
min j , s [ min c 1 ∑ x ∈ R 1 ( y i − c 1 ) 2 + min c 2 ∑ x ∈ R 2 ( y i − c 2 ) 2 ] \min\limits_{j,s}[\min\limits_{c_1}\sum\limits_{x \in R_1}(y_i - c1)^2 + \min\limits_{c_2}\sum\limits_{x \in R_2}(y_i - c2)^2] j,smin[c1minx∈R1∑(yi−c1)2+c2minx∈R2∑(yi−c2)2]
第二步:这里设定的输出值为训练数据输出的均方差
$c_1 = ave(y_i | x_i \in R_1) \quad c_2 = ave(y_i | x_i \in R_2) $
第三步: 对已经划分的两个子区域,再次重复步骤1,2,知道满足停止条件,生成有M个区域的决策树。
分类树
基尼指数
分类问题中假设有K个类,样本点属于k类的概率为 p k p_k pk,则概率分布的基尼系数为:
G i n i ( p ) = ∑ k = 1 K p k ( 1 − p k ) = 1 − ∑ k = 1 K p k 2 Gini(p)=\sum\limits_{k=1}^{K}p_k(1 - p_k) = 1 - \sum\limits_{k=1}^{K}p_k^2 Gini(p)=k=1∑Kpk(1−pk)=1−k=1∑Kpk2
对于给定的样本集合D,其基尼指数为:
G i n i ( D ) = 1 − ∑ k = 1 K ( ∣ C k ∣ ∣ D ∣ ) 2 Gini(D)=1-\sum\limits_{k=1}^{K}(\dfrac{|C_k|}{|D|})^2 Gini(D)=1−k=1∑K(∣D∣∣Ck∣)2,这里 C k C_k Ck表示D中属于k类的数量。
基尼系数表示了集合D的不确定性,Gini(D, A)表示D作了A分割成 D 1 D 2 D_1 \quad D_2 D1D2后的不确定性,基尼系数越大,不确定性越大。
其中 G i n i ( D , A ) = D 1 D G i n i ( D 1 ) + D 2 D G i n i ( D 2 ) Gini(D, A)=\dfrac{D_1}{D}Gini(D_1) + \dfrac{D_2}{D}Gini(D_2) Gini(D,A)=DD1Gini(D1)+DD2Gini(D2)
分类树的训练
这个和回归树的方式基本一样,只是损失定义从最小二乘转变为基尼指数。
第一步: 对输入数据D的每一个特征和可能的取值,做分类A并计算Gini(D, A)
第二步: 取Gini(D, A)最小的一组数据,作为本次的最有特征和最优切分点
第三步: 对上述划分的结果,迭代步骤1,2
第四步: 生成CART决策树(分类)
代码实现(回归树,基于sklearn)
# -*- coding: utf-8 -*-
import numpy as np
import matplotlib.pyplot as plt
from sklearn.tree import DecisionTreeRegressor
def _test_cart_regresssion():
index = np.linspace(0, 10, 200);
delta = np.random.rand()
index.shape = (200, 1)
y_test = 0.3*index + np.sin(index) + delta
clf = DecisionTreeRegressor(max_depth=4)
"""
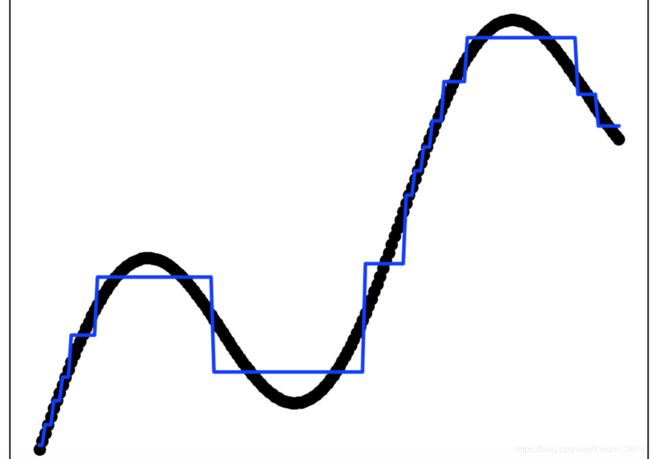
这里的深度为4,相当于回归的时候分了4次,划分为2^4=16个区域
"""
clf.fit(index, y_test)
y_pred = clf.predict(index)
plt.scatter(index, y_test, color='black',marker='o')
plt.plot(index, y_pred, color='blue', linewidth=2)
plt.xticks(())
plt.yticks(())
plt.show()
pass;
"""
说明:
CART算法回归树及决策树的例子《CART算法》
作者:fredric
日期:2018-11-4
"""
if __name__ == "__main__":
_test_cart_regresssion()