深度学习中的Batch Normalization

在看 ladder network(https://arxiv.org/pdf/1507.02672v2.pdf) 时初次遇到batch normalization（BN）. 文中说BN能加速收敛等好处，但是并不理解，然后就在网上搜了些关于BN的资料。

看了知乎上关于深度学习中 Batch Normalization为什么效果好？ 和CSDN上一个关于Batch Normalization 的学习笔记，总算对BN有一定的了解了。这里只是总结一下BN的具体操作流程，对于BN更深层次的理解，为什么要BN，BN是否真的有效也还在持续学习和实验中。

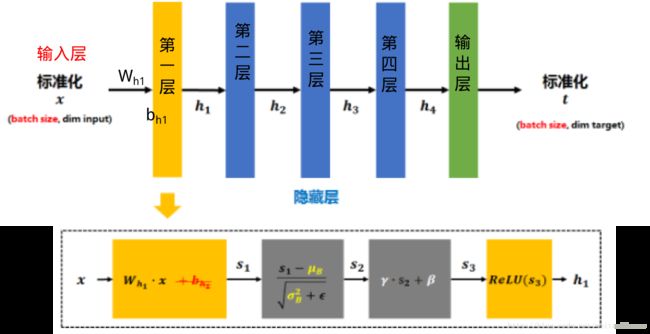
BN就是在神经网络的训练过程中对每层的输入数据加一个标准化处理。 

传统的神经网络，只是在将样本xx输入输入层之前对xx进行标准化处理（减均值，除标准差），以降低样本间的差异性。BN是在此基础上，不仅仅只对输入层的输入数据xx进行标准化，还对每个隐藏层的输入进行标准化。

标准化后的xx乘以权值矩阵Wh1Wh1加上偏置bh1bh1得到第一层的输入wh1x+bh1wh1x+bh1,经过激活函数得到h1=ReLU(wh1x+bh1)h1=ReLU(wh1x+bh1)，然而加入BN后, h1h1的计算流程如虚线框所示： 
1. 矩阵xx先经过Wh1Wh1的线性变换后得到s1s1 (注：因为减去batch的平均值μBμB后，bb的作用会被抵消掉，所提没必要加入bb了）

1. 将s1s1再减去batch的平均值μBμB，并除以batch的标准差σ2B+ϵ−−−−−√σB2+ϵ得到s2s2. ϵϵ是为了避免除数为0时所使用的微小正数。 
   其中μB=1m∑mi=0Wh1xiμB=1m∑i=0mWh1xi 
   σ2B=1m∑mi=0(Wh1xi−μB)2σB2=1m∑i=0m(Wh1xi−μB)2 
   (注：由于这样做后s2s2基本会被限制在正态分布下，使得网络的表达能力下降。为解决该问题，引入两个新的参数：γγ,ββ. γγ和ββ是在训练时网络自己学习得到的。）

2. 将s2s2乘以γγ调整数值大小，再加上ββ增加偏移后得到s3s3

3. s3s3经过激活函数后得到h1h1

需要注意的是，上述的计算方法用于在训练过程中。在测试时，所使用的μμ和σ2σ2是整个训练集的均值μpμp和方差σ2pσp2. 整个训练集的均值μpμp和方差σ2pσp2的值通常是在训练的同时用移动平均法来计算的.

在看具体代码之前，先来看两个求平均值函数的用法：

mean, variance = tf.nn.moments(x, axes, name=None, keep_dims=False)

这个函数的输入参数x表示样本，形如[batchsize, height, width, kernels] 
axes表示在哪个维度上求解，是个list 
函数输出均值和方差

'''
batch = np.array(np.random.randint(1, 100, [10, 5]))开始这里没有定义数据类型，batch的dtype=int64,导致后面sess.run([mm,vv])时老报InvalidArgumentError错误，原因是tf.nn.moments中的计算要求参数是float的
'''
batch = np.array(np.random.randint(1, 100, [10, 5]),dtype=np.float64)
mm, vv=tf.nn.moments(batch,axes=[0])#按维度0求均值和方差
#mm, vv=tf.nn.moments(batch,axes=[0,1])求所有数据的平均值和方差
sess = tf.Session()
print batch
print sess.run([mm, vv])#一定要注意参数类型
sess.close()

输出结果：

[[ 53.   9.  67.  30.  69.]
 [ 79.  25.   7.  80.  16.]
 [ 77.  67.  60.  30.  85.]
 [ 45.  14.  92.  12.  67.]
 [ 32.  98.  70.  98.  48.]
 [ 45.  89.  73.  73.  80.]
 [ 35.  67.  21.  77.  63.]
 [ 24.  33.  56.  85.  17.]
 [ 88.  43.  58.  82.  59.]
 [ 53.  23.  34.   4.  33.]]
[array([ 53.1,  46.8,  53.8,  57.1,  53.7]), array([  421.09,   896.96,   598.36,  1056.69,   542.61])]

ema = tf.train.ExponentialMovingAverage(decay) 求滑动平均值需要提供一个衰减率。该衰减率用于控制模型更新的速度，ExponentialMovingAverage 对每一个（待更新训练学习的）变量（variable）都会维护一个影子变量（shadow variable）。影子变量的初始值就是这个变量的初始值，

shadow_variable=decay×shadow_variable+(1−decay)×variable

由上述公式可知， decay 控制着模型更新的速度，越大越趋于稳定。实际运用中，decay 一般会设置为十分接近 1 的常数（0.99或0.999）。为了使得模型在训练的初始阶段更新得更快，ExponentialMovingAverage 还提供了 num_updates 参数来动态设置 decay 的大小：

decay=min{decay,1+num_updates10+num_updates}decay=min{decay,1+num_updates10+num_updates}

对于滑动平均值我是这样理解的（也不知道对不对，如果有觉得错了的地方希望能帮忙指正）

假设有一串时间序列 {a1,a2,a3,⋯,at,at+1,⋯,}{a1,a2,a3,⋯,at,at+1,⋯,} 
t时刻的平均值为mvt=a1+a2+⋯+attmvt=a1+a2+⋯+att 
t+1时刻的平均值为mvt+1=a1+a2+⋯+at+at+1t+1=tmvt+at+1t+1=tt+1mvt+1t+1at+1mvt+1=a1+a2+⋯+at+at+1t+1=tmvt+at+1t+1=tt+1mvt+1t+1at+1 
令decay=tt+1tt+1, 则mvt+1=decay∗mvt+(1−decay)∗at+1mvt+1=decay∗mvt+(1−decay)∗at+1

import tensorflow as tf
graph=tf.Graph()
with graph.as_default():
    w = tf.Variable(dtype=tf.float32,initial_value=1.0)
    ema = tf.train.ExponentialMovingAverage(0.9)
    update = tf.assign_add(w, 1.0)

    with tf.control_dependencies([update]):
        ema_op = ema.apply([w])#返回一个op,这个op用来更新moving_average #这句和下面那句不能调换顺序

    ema_val = ema.average(w)#此op用来返回当前的moving_average,这个参数不能是list

with tf.Session(graph=graph) as sess:
    sess.run(tf.initialize_all_variables())
    for i in range(3):
        print i
        print 'w_old=',sess.run(w)
        print sess.run(ema_op)
        print 'w_new=', sess.run(w)
        print sess.run(ema_val)
        print '**************'

输出：

0
w_old= 1.0
None
w_new= 2.0#在执行ema_op时先执行了对w的更新
1.1  #0.9*1.0+0.1*2.0=1.1
**************
1
w_old= 2.0
None
w_new= 3.0
1.29  #0.9*1.1+0.1*3.0=1.29
**************
2
w_old= 3.0
None
w_new= 4.0
1.561  #0.9*1.29+0.1*4.0=1.561

关于加入了batch Normal的对mnist手写数字分类的nn网络完整代码：

import tensorflow as tf
#import input_data
from tqdm import tqdm
import numpy as np
import math
from six.moves import cPickle as pickle
#数据预处理
pickle_file = '/home/sxl/tensor学习/My Udacity/notM/notMNISTs.pickle'
#为了加速计算，这个是经过处理的小样本mnist手写数字，这个数据可在[这里](http://download.csdn.net/detail/whitesilence/9908115)下载
with open(pickle_file, 'rb') as f:
  save = pickle.load(f)
  train_dataset = save['train_dataset']
  train_labels = save['train_labels']
  valid_dataset = save['valid_dataset']
  valid_labels = save['valid_labels']
  test_dataset = save['test_dataset']
  test_labels = save['test_labels']
  del save  # hint to help gc free up memory
  print('Training set', train_dataset.shape, train_labels.shape)
  print('Validation set', valid_dataset.shape, valid_labels.shape)
  print('Test set', test_dataset.shape, test_labels.shape)

image_size = 28
num_labels = 10

def reformat(dataset, labels):
    dataset = dataset.reshape((-1, image_size * image_size)).astype(np.float32)
    # Map 0 to [1.0, 0.0, 0.0 ...], 1 to [0.0, 1.0, 0.0 ...]
    labels = (np.arange(num_labels) == labels[:, None]).astype(np.float32)
    return dataset, labels

train_dataset, train_labels = reformat(train_dataset, train_labels)
valid_dataset, valid_labels = reformat(valid_dataset, valid_labels)
test_dataset, test_labels = reformat(test_dataset, test_labels)
print('Training set', train_dataset.shape, train_labels.shape)
print('Validation set', valid_dataset.shape, valid_labels.shape)
print('Test set', test_dataset.shape, test_labels.shape)

#创建一个7层网络
layer_sizes = [784, 1000, 500, 250, 250,250,10]
L = len(layer_sizes) - 1  # number of layers
num_examples = train_dataset.shape[0]
num_epochs = 100
starter_learning_rate = 0.02
decay_after = 15  # epoch after which to begin learning rate decay
batch_size = 120
num_iter = (num_examples/batch_size) * num_epochs  # number of loop iterations

x = tf.placeholder(tf.float32, shape=(None, layer_sizes[0]))
outputs = tf.placeholder(tf.float32)
testing=tf.placeholder(tf.bool)
learning_rate = tf.Variable(starter_learning_rate, trainable=False)

def bi(inits, size, name):
    return tf.Variable(inits * tf.ones([size]), name=name)

def wi(shape, name):
    return tf.Variable(tf.random_normal(shape, name=name)) / math.sqrt(shape[0])

shapes = zip(layer_sizes[:-1], layer_sizes[1:])  # shapes of linear layers

weights = {'W': [wi(s, "W") for s in shapes],  # feedforward weights
           # batch normalization parameter to shift the normalized value
           'beta': [bi(0.0, layer_sizes[l+1], "beta") for l in range(L)],
           # batch normalization parameter to scale the normalized value
           'gamma': [bi(1.0, layer_sizes[l+1], "beta") for l in range(L)]}

ewma = tf.train.ExponentialMovingAverage(decay=0.99)  # to calculate the moving averages of mean and variance
bn_assigns = []  # this list stores the updates to be made to average mean and variance

def batch_normalization(batch, mean=None, var=None):
    if mean is None or var is None:
        mean, var = tf.nn.moments(batch, axes=[0])
    return (batch - mean) / tf.sqrt(var + tf.constant(1e-10))

# average mean and variance of all layers
running_mean = [tf.Variable(tf.constant(0.0, shape=[l]), trainable=False) for l in layer_sizes[1:]]
running_var = [tf.Variable(tf.constant(1.0, shape=[l]), trainable=False) for l in layer_sizes[1:]]

def update_batch_normalization(batch, l):
    "batch normalize + update average mean and variance of layer l"
    mean, var = tf.nn.moments(batch, axes=[0])
    assign_mean = running_mean[l-1].assign(mean)
    assign_var = running_var[l-1].assign(var)
    bn_assigns.append(ewma.apply([running_mean[l-1], running_var[l-1]]))
    with tf.control_dependencies([assign_mean, assign_var]):
        return (batch - mean) / tf.sqrt(var + 1e-10)


def eval_batch_norm(batch,l):
    mean = ewma.average(running_mean[l - 1])
    var = ewma.average(running_var[l - 1])
    s = batch_normalization(batch, mean, var)
    return s

def net(x,weights,testing=False):
    d={'m': {}, 'v': {}, 'h': {}}
    h=x
    for l in range(1, L+1):
        print "Layer ", l, ": ", layer_sizes[l-1], " -> ", layer_sizes[l]
        d['h'][l-1]=h
        s= tf.matmul(d['h'][l-1], weights['W'][l-1])
        m, v = tf.nn.moments(s, axes=[0])
        if testing:
            s=eval_batch_norm(s,l)
        else:
            s=update_batch_normalization(s, l)
        s=weights['gamma'][l-1] * s + weights["beta"][l-1]
        if l == L:
            # use softmax activation in output layer
            h = tf.nn.softmax(s)
        else:
            h= tf.nn.relu(s)
        d['m'][l]=m
        d['v'][l]=v
    d['h'][l]=h
    return h,d

y,_=net(x,weights)

cost = -tf.reduce_mean(tf.reduce_sum(outputs*tf.log(y), 1))

correct_prediction = tf.equal(tf.argmax(y, 1), tf.argmax(outputs, 1))  # no of correct predictions

accuracy = tf.reduce_mean(tf.cast(correct_prediction, "float")) * tf.constant(100.0)


train_step = tf.train.AdamOptimizer(learning_rate).minimize(cost)

# add the updates of batch normalization statistics to train_step
bn_updates = tf.group(*bn_assigns)
with tf.control_dependencies([train_step]):
    train_step = tf.group(bn_updates)

print "===  Starting Session ==="

sess = tf.Session()
init = tf.initialize_all_variables()
sess.run(init)

i_iter = 0
print "=== Training ==="
#print "Initial Accuracy: ", sess.run(accuracy, feed_dict={x: test_dataset, outputs: test_labels, testing: True}), "%"

for i in tqdm(range(i_iter, num_iter)):
    #images, labels = mnist.train.next_batch(batch_size)
    start = (i * batch_size) % num_examples
    images=train_dataset[start:start+batch_size,:]
    labels=train_labels[start:start+batch_size,:]
    sess.run(train_step, feed_dict={x: images, outputs: labels})
    if (i > 1) and ((i+1) % (num_iter/num_epochs) == 0):#i>1且完成了一个epochs,即所有数据训练完一遍
        epoch_n = i/(num_examples/batch_size)#第几个epochs
        perm = np.arange(num_examples)
        np.random.shuffle(perm)
        train_dataset = train_dataset[perm]#所有训练数据迭代完一次后，对训练数据进行重排，避免下一次迭代时取的是同样的数据
        train_labels = train_labels[perm]
        if (epoch_n+1) >= decay_after:
            # decay learning rate
            # learning_rate = starter_learning_rate * ((num_epochs - epoch_n) / (num_epochs - decay_after))
            ratio = 1.0 * (num_epochs - (epoch_n+1))  # epoch_n + 1 because learning rate is set for next epoch
            ratio = max(0, ratio / (num_epochs - decay_after))
            sess.run(learning_rate.assign(starter_learning_rate * ratio))
        print "Train Accuracy: ",sess.run(accuracy,feed_dict={x: images, outputs: labels})

print "Final Accuracy: ", sess.run(accuracy, feed_dict={x: test_dataset, outputs: test_labels, testing: True}), "%"

sess.close()

 

关于batch normal 的另一参考资料http://blog.csdn.net/intelligence1994/article/details/53888270 
tensorflow常用函数介绍http://blog.csdn.net/wuqingshan2010/article/details/71056292

参考：https://blog.csdn.net/whitesilence/article/details/75667002