CNN卷积神经网络手写数字识别实例及代码详解

本文的代码来自githup的Deep Learning的toolbox，是用Matlab实现的。感谢该toolbox的作者付出和分享。

我在应该该代码进行训练时，出现一些报错，如expand函数应用不对，sigm函数和flipall函数未定义等问题，对这些问题进行了修正，完成网络训练和验证。

本文mnist_uint8.mat的获取可以参照我的另一篇博客：MNIST数据库处理--matlab生成mnist_uint8.mat   http://blog.csdn.net/fuwenyan/article/details/53954615

本文作者：非文艺小燕儿，VivienFu，

欢迎大家转载适用，请注明出处。http://blog.csdn.net/fuwenyan?viewmode=contents http://blog.csdn.net/fuwenyan?viewmode=contents

学习该代码需要一定的CNN理论基础。

目的：实现手写数字识别

数据集：MNIST数据集，60000张训练图像，10000张测试图像，每张图像size为28*28

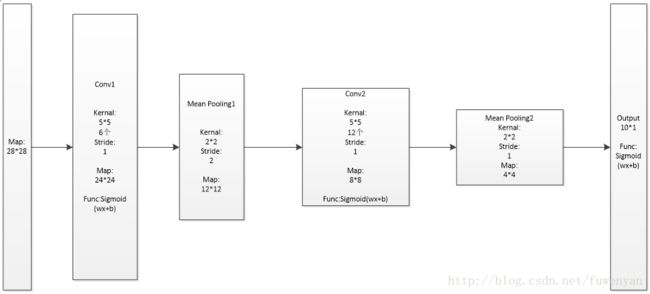
网络层级结构概述：5层神经网络

Input layer: 输入数据为原始训练图像

Conv1：6个5*5的卷积核，步长Stride为1

Pooling1：卷积核size为2*2，步长Stride为2

Conv2：12个5*5的卷积核，步长Stride为1

Pooling2：卷积核size为2*2，步长Stride为2

Output layer：输出为10维向量

网络层级结构示意图如下：

 

 

 

 

 

代码流程概述：

（1）获取训练数据和测试数据；

（2）定义网络层级结构；

（3）初始设置网络参数（权重W，偏向b）cnnsetup(cnn, train_x, train_y)

（4）训练超参数opts定义（学习率，batchsize，epoch）

（5）网络训练之前向运算cnnff(net, batch_x)

（6）网络训练之反向传播cnnbp(net, batch_y)

（7）网络训练之参数更新cnnapplygrads(net, opts)

（8）重复（5）（6）（7），直至满足epoch

（9）网络测试cnntest(cnn, test_x, test_y)

 

 

 详细代码及我的注释

 

cnnexamples.m

clear all; close all; clc;    
load mnist_uint8;  
  
train_x = double(reshape(train_x',28,28,60000))/255;  %数据归一化至[0 1]之间
test_x = double(reshape(test_x',28,28,10000))/255;  %数据归一化至[0 1]之间
train_y = double(train_y');  
test_y = double(test_y');  
 
%% ex1   
%will run 1 epoch in about 200 second and get around 11% error.   
%With 100 epochs you'll get around 1.2% error  
  
cnn.layers = {  
    struct('type', 'i') %input layer  
    struct('type', 'c', 'outputmaps', 6, 'kernelsize', 5) %convolution layer，6个5*5的卷积核，可以得到6个outputmaps  
    struct('type', 's', 'scale', 2) %sub sampling layer  ，2*2的下采样卷积核
    struct('type', 'c', 'outputmaps', 12, 'kernelsize', 5) %convolution layer ，12个5*5的卷积核，可以得到12个outputmaps  


    struct('type', 's', 'scale', 2) %subsampling layer    ，2*2的下采样卷积核
};  %定义了一个5层神经网络，还有一个输出层，并未在这里定义。
  
cnn = cnnsetup(cnn, train_x, train_y);  %通过该函数，对网络初始权重矩阵和偏向进行初始化
  
opts.alpha = 1;  % 学习率
 
opts.batchsize = 50; %每batchsize张图像一起训练一轮，调整一次权值。  
% 训练次数，用同样的样本集。我训练的时候：  
% 1的时候 11.41% error  
% 5的时候 4.2% error  
% 10的时候 2.73% error  
opts.numepochs = 10;  %每个epoch内，对所有训练数据进行训练，更新（训练图像个数/batchsize）次网络参数
  
cnn = cnntrain(cnn, train_x, train_y, opts);  %网络训练
  
 [er_test, bad_test] = cnntest(cnn, test_x, test_y);  %网络测试


  
%plot mean squared error  
plot(cnn.rL);  
%show test error  
disp(['10000 test images ' num2str(er_test*100) '% error']);  


 [er_train, bad_train] = cnntest(cnn, train_x, train_y);  %网络测试
disp(['60000 train images ' num2str(er_train*100) '% error']);  

 

cnnsetup.m

function net = cnnsetup(net, x, y)  
    inputmaps = 1;  %每个batch中的所有图片并行运算，但处理方法都是相同的。所以对于输入层inputmaps=1，对于其他层，inputmaps=上一层的outputmaps


    mapsize = size(squeeze(x(:, :, 1)));  %squeeze(x(:, :, 1))相当于取第一个图像样本后，再把第三维移除，得到一张图象size[28 28]
  
    for l = 1 : numel(net.layers)   %  layer  %对每一层网络进行遍历处理，net.layers中有五个struct类型的元素，此处numel(net.layers)=5
        if strcmp(net.layers{l}.type, 's')  %下采样层（也叫pooling层）处理，获取下采样后的mapsize，和初始偏置
            mapsize = floor(mapsize / net.layers{l}.scale);  %此处下采样的步长stride=scale，
            for j = 1 : inputmaps  %此处不应该是outputmap的数吗?对于Pooling层，inputmaps=outputmaps
                net.layers{l}.b{j} = 0; % 将偏置初始化为0  
            end  
        end  %Pooling层没有权重矩阵初始化？
        if strcmp(net.layers{l}.type, 'c') %卷积层处理，获取下一层的mapsize，权重的初始化和偏置的初始化，下一层的inputmaps
            % 旧的mapsize保存的是上一层的特征map的大小，那么如果卷积核的移动步长是1，那用  
            % kernelsize*kernelsize大小的卷积核卷积上一层的特征map后，得到的新的map的大小就是下面这样  
            mapsize = mapsize - net.layers{l}.kernelsize + 1;  %卷积步长stride为1的情况
            % 该层需要学习的参数个数。每张特征map是一个(后层特征图数量)*(用来卷积的patch图的大小)  
            % 因为是通过用一个核窗口在上一个特征map层中移动（核窗口每次移动1个像素），遍历上一个特征map  
            % 层的每个神经元。核窗口由kernelsize*kernelsize个元素组成，每个元素是一个独立的权值，所以  
            % 就有kernelsize*kernelsize个需要学习的权值，再加一个偏置值。另外，由于是权值共享，也就是  
            % 说同一个特征map层是用同一个具有相同权值元素的kernelsize*kernelsize的核窗口去感受输入上一  
            % 个特征map层的每个神经元得到的，所以同一个特征map，它的权值是一样的，共享的，权值只取决于  
            % 核窗口。然后，不同的特征map提取输入上一个特征map层不同的特征，所以采用的核窗口不一样，也  
            % 就是权值不一样，所以outputmaps个特征map就有（kernelsize*kernelsize+1）* outputmaps那么多的权值了  
            % 但这里fan_out只保存卷积核的权值W，偏置b在下面独立保存  
            fan_out = net.layers{l}.outputmaps * net.layers{l}.kernelsize ^ 2;  %计算卷积核权重参数的总数，对于Conv1：6*5*5=150，对于Conv2：12*5*5=300
            for j = 1 : net.layers{l}.outputmaps  %  output map  %Conv1：6；Conv2：12
                % fan_out保存的是对于上一层的一张特征map，我在这一层需要对这一张特征map提取outputmaps种特征， 所需要的权重总数 
                % 提取每种特征用到的卷积核不同，所以fan_out保存的是这一层输出新的特征需要学习的参数个数  
                % 而，fan_in保存的是，我在这一层，要连接到上一层中所有的特征map，然后用fan_out保存的提取特征  
                % 的权值来提取他们的特征。也即是对于每一个当前层特征图，有多少个参数链到前层  
                fan_in = inputmaps * net.layers{l}.kernelsize ^ 2;  %每一个inputmap经过outputmaps个卷积核提取outputmaps种特征，得到outputmaps个输出。         不同的inputmap对应不同的卷积核
                for i = 1 : inputmaps  %  input map  
                    % 随机初始化权值，也就是共有outputmaps个卷积核，对上层的每个特征map，都需要用这么多个卷积核  
                    % 去卷积提取特征。  
                    % rand(n)是产生n×n的 0-1之间均匀取值的数值的矩阵，再减去0.5就相当于产生-0.5到0.5之间的随机数  
                    % 再 *2 就放大到 [-1, 1]。然后再乘以后面那一数，why？  
                    % 反正就是将卷积核每个元素初始化为[-sqrt(6 / (fan_in + fan_out)), sqrt(6 / (fan_in + fan_out))]  
                    % 之间的随机数。因为这里是权值共享的，也就是对于一张特征map，所有感受野位置的卷积核都是一样的  
                    % 所以只需要保存的是 inputmaps * outputmaps 个卷积核。  
                    net.layers{l}.k{i}{j} = (rand(net.layers{l}.kernelsize) - 0.5) * 2 * sqrt(6 / (fan_in + fan_out));  %为什么要乘以后面的数？
                end  
                net.layers{l}.b{j} = 0; % 将偏置初始化为0  
            end  
            % 只有在卷积层的时候才会改变特征map的个数，pooling的时候不会改变个数。这层输出的特征map个数就是  
            % 输入到下一层的特征map个数  
            inputmaps = net.layers{l}.outputmaps;   
        end  
    end  
      %下面开始初始化输出层网络参数。输出层与前一层之间是全连接。
    % 这一层的上一层是经过pooling后的层，包含有inputmaps个特征map。每个特征map的大小是mapsize。  
    % 所以，该层的神经元个数是 inputmaps * （每个特征map的大小）  
    % For vectors, prod(X) 是X元素的连乘积  
    fvnum = prod(mapsize) * inputmaps;  %输出层前一层的神经元个数，即像素数目 5*5*12=300
    % onum 是标签的个数，也就是输出层神经元的个数。你要分多少个类，自然就有多少个输出神经元  
    onum = size(y, 1);  % y为10*60000的矩阵，10表示10个类别，60000表示训练图像的个数，如第一张图像为1，则y(:,1)=[0 1 0 0 0 0 0 0 0 0]
   
    net.ffb = zeros(onum, 1);  %初始化输出层的偏向b为0
    net.ffW = (rand(onum, fvnum) - 0.5) * 2 * sqrt(6 / (onum + fvnum));  %初始化输出层与前一层的权重矩阵，为全连接层FC，size为[10 300]
end  

 

cnntrain.m

function net = cnntrain(net, x, y, opts)  
    m = size(x, 3); % m 保存的是 训练样本个数  %本次应用60000个训练样本
    numbatches = m / opts.batchsize;  %本次应用batchsize为50，numbatches =1200
    % rem: Remainder after division. rem(x,y) is x - n.*y 相当于求余  
    % rem(numbatches, 1) 就相当于取其小数部分，如果为0，就是整数  
    if rem(numbatches, 1) ~= 0  %检验训练样本数是否能被batchsize整除
        error('numbatches not integer');  
    end  
      
    net.rL = [];  %这是什么
    for i = 1 : opts.numepochs  %本次应用opts.numepochs=10
        disp(['epoch ' num2str(i) '/' num2str(opts.numepochs)]);  %进展打印，当前运行到第i个epoch
        % tic 和 toc 是用来计时的，计算这两条语句之间所耗的时间  
        tic;  
        % P = randperm(N) 返回[1, N]之间所有整数的一个随机的序列，例如  
        % randperm(6) 可能会返回 [2 4 5 6 1 3]  
        % 这样就相当于把原来的样本排列打乱，再挑出一些样本来训练  
        kk = randperm(m);  %每一轮epoch都要将所有训练集进行随机打乱
        for l = 1 : numbatches %每个batch训练后更新一次网络参数
            disp(['batch ' num2str(l) '/' num2str(numbatches)]);  %进展打印，当前运行到第l个batch
            batch_x = x(:, :, kk((l - 1) * opts.batchsize + 1 : l * opts.batchsize));  %每次取一个batchsize（50）张图像进行同步训练
            batch_y = y(:,    kk((l - 1) * opts.batchsize + 1 : l * opts.batchsize));  
  
            net = cnnff(net, batch_x); % Feedforward前向传递，在当前的网络权值和网络输入下计算网络的输出，包涵每一层的输入输出 
 
            net = cnnbp(net, batch_y); % Backpropagation反向传播，得到损失函数对网络参数（权重和偏向）的梯度（偏导）  


            net = cnnapplygrads(net, opts);  %根据损失函数对网络参数（权重和偏向）的梯度（偏导），更新网络参数


            if isempty(net.rL)  
                net.rL(1) = net.L; % 代价函数值，也就是误差值，net.L为网络均方误差的1/2  
            end  
            net.rL(end + 1) = 0.99 * net.rL(end) + 0.01 * net.L; % 保存历史的误差值，以便画图分析，为什么采用比例求和的方式？  
        end  
        toc;  %打印每个epoch执行时间
    end  
      
end  

 

 

cnnff.m

function net = cnnff(net, x)  
    n = numel(net.layers); % 层数  
    net.layers{1}.a{1} = x; % 网络的第一层就是输入，包含了batchsize个训练图像，并行训练
    inputmaps = 1; % 输入层只有一个特征map，也就是输入的一张图像，虽然实际输入是batchsize个训练图像，由于是并行运算，所以可以理解为一条线上只有一张图像  
  
    for l = 2 : n   %  对输入层与输出层之间的每一层进行处理  
        if strcmp(net.layers{l}.type, 'c') % 卷积层  
            %  !!below can probably be handled by insane matrix operations  
            % 对每一个输入map，或者说我们需要用outputmaps个不同的卷积核去卷积图像  
            for j = 1 : net.layers{l}.outputmaps   %  for each output map   %第一个卷积层6个outputmaps,第二个卷积层12个outputmaps
                %  create temp output map  
                % 对上一层的每一张特征map，卷积后的特征map的大小就是   
                % （输入map宽 - 卷积核的宽 + 1）* （输入map高 - 卷积核高 + 1）  
                % 对于这里的层，因为每层都包含多张特征map，对应的索引保存在每层map的第三维  
                % 所以，这里的z保存的就是该层中所有的特征map了  
                z = zeros(size(net.layers{l - 1}.a{1}) - [net.layers{l}.kernelsize - 1 net.layers{l}.kernelsize - 1 0]);  %初始l层输出特征map，第一个卷积层map的size为[28 28 50]-[4，4，0]=[24 24 50],第三维为batchsize
                for i = 1 : inputmaps   %  for each input map 每个卷积核对所有inputmaps进行卷积后，求和，得到一个该卷积核对应的outputmap
                    %  convolve with corresponding kernel and add to temp output map  
                    % 将上一层的每一个特征map（也就是这层的输入map）与该层的卷积核进行卷积  
                    % 然后将对上一层特征map的所有结果加起来。也就是说，当前层的一张特征map，是  
                    % 用一种卷积核去卷积上一层中所有的特征map，然后所有特征map对应位置的卷积值的和  
                    % 另外，有些论文或者实际应用中，并不是与全部的特征map链接的，有可能只与其中的某几个连接  
                    z = z + convn(net.layers{l - 1}.a{i}, net.layers{l}.k{i}{j}, 'valid');   % k{i}{j}为卷积核，第一个卷积层得到的z的size为[24 24 50]
                end  
                %  add bias, pass through nonlinearity  
                % 加上对应位置的基b，然后再用sigmoid函数算出特征map中每个位置的激活值，作为该层输出特征map  
                net.layers{l}.a{j} = sigm(z + net.layers{l}.b{j});  
            end  
            %  set number of input maps to this layers number of outputmaps  
            inputmaps = net.layers{l}.outputmaps;  
        elseif strcmp(net.layers{l}.type, 's') % 下采样层，采用均值进行下采样，下采样层无激励函数  
            for j = 1 : inputmaps  
                %  !! replace with variable  
                % 例如我们要在scale=2的域上面执行mean pooling，那么可以卷积大小为2*2，每个元素都是1/4的卷积核  
                z = convn(net.layers{l - 1}.a{j}, ones(net.layers{l}.scale) / (net.layers{l}.scale ^ 2), 'valid');   
                % 因为convn函数的默认卷积步长为1，而pooling操作的域是没有重叠的，所以对于上面的卷积结果  
                % 最终pooling的结果需要从上面得到的卷积结果中以scale=2为步长，跳着把mean pooling的值读出来  
                net.layers{l}.a{j} = z(1 : net.layers{l}.scale : end, 1 : net.layers{l}.scale : end, :);  
            end  
        end  
    end  
  
%以下进行输出层的处理，输出层与前一层是全连接。
%输出层10个神经元，分别代表10类图像。
%输出层的前一层神经元个数为所有特征map像素点的和，也就是每个像素点都是一个神经元
    %  concatenate all end layer feature maps into vector   
    net.fv = [];  %存放reshape后的输出层前一层的特征map（所有特征map一起）
    for j = 1 : numel(net.layers{n}.a) % 输出层前一层的特征map的个数  %此应用为12个
        sa = size(net.layers{n}.a{j}); % 第j个特征map的大小 %考虑batchsize为[4 4 50]
        % 将所有的特征map拉成一条列向量。还有一维就是对应的样本索引。每个样本一列，每列为对应的特征向量  
        net.fv = [net.fv; reshape(net.layers{n}.a{j}, sa(1) * sa(2), sa(3))];  %由最后一层特征map reshape得到，其size为[16 50]
    end  %最后得到的net.fv的size为[numel(net.layers{n}.a)*16  50],即把输出层前一层的所有特征map拉成一条列向量
    %  feedforward into output perceptrons  
    % 计算网络的最终输出值。sigmoid(W*X + b)，注意是同时计算了batchsize个样本的输出值  
    net.o = sigm(net.ffW * net.fv + repmat(net.ffb, 1, size(net.fv, 2)));  %输出值的size为[10 50]，10为10类上的输出，50为batchsize
  
end

 

cnnbp.m

function net = cnnbp(net, y)  
    n = numel(net.layers); % 网络层数 %5 
    net.e = net.o - y;   %计算网络运算输出与实际分类之间的偏差，size为[10 50]
    %  loss function  
    net.L = 1/2* sum(net.e(:) .^ 2) / size(net.e, 2);  %方差损失函数，为了方便求导取了1/2。将一个batch内的所有图像偏差一起计算并取均值
  
    %%  backprop deltas  
    net.od = net.e .* (net.o .* (1 - net.o));   %  输出层的梯度  net.e为损失函数对net.o的导数，(net.o .* (1 - net.o))为sigmoid输出对输入的导数,size[10 50]
    % 残差 反向传播回 前一层  
    net.fvd = (net.ffW' * net.od);              %  feature vector delta  %输出层前一层的梯度，是下采样层，f(x)=x，没有sigmoid激励函数,size [16*12 50]
    if strcmp(net.layers{n}.type, 'c')         %  only conv layers has sigm function  
        net.fvd = net.fvd .* (net.fv .* (1 - net.fv)); %如果是卷积层，有sigmoid激励函数，需要追加乘上sigmoid的导数 ,size [16*12 50]
    end  
  
    %  reshape feature vector deltas into output map style  
    sa = size(net.layers{n}.a{1}); % 最后一层特征map的大小。这里的最后一层都是指输出层的前一层  
    fvnum = sa(1) * sa(2); % 因为是将最后一层特征map拉成一条向量，所以对于一个样本来说，特征维数是这样  
    for j = 1 : numel(net.layers{n}.a) % 最后一层的特征map的个数  
        % 在fvd里面保存的是所有样本的特征向量（在cnnff.m函数中用特征map拉成的），所以这里需要重新  
        % 变换回来特征map的形式。d 保存的是 delta，也就是 灵敏度 或者 残差  
        net.layers{n}.d{j} = reshape(net.fvd(((j - 1) * fvnum + 1) : j * fvnum, :), sa(1), sa(2), sa(3));  
    end  
  
    % 对于 输出层前面的层（与输出层计算残差的方式不同）  
    for l = (n - 1) : -1 : 1  
        if strcmp(net.layers{l}.type, 'c')  
            for j = 1 : numel(net.layers{l}.a) % 该层特征map的个数  
                % net.layers{l}.d{j} 保存的是 第l层 的 第j个 map 的 灵敏度map。 也就是每个神经元节点的delta的值  
                for k = 1:size(net.layers{l + 1}.d{j}, 3)  
                    net.layers{l}.d{j}(:,:,k) = net.layers{l}.a{j}(:,:,k) .* (1 - net.layers{l}.a{j}(:,:,k)) .*  kron(net.layers{l + 1}.d{j}(:,:,k), ones(net.layers{l + 1}.scale)) / net.layers{l + 1}.scale ^ 2;  
                end  
%                 net.layers{l}.d{j} = net.layers{l}.a{j} .* (1 - net.layers{l}.a{j}) .* (expand(net.layers{l + 1}.d{j}, [net.layers{l + 1}.scale net.layers{l + 1}.scale 1]) / net.layers{l + 1}.scale ^ 2);  %卷积层input和output map数不一定相等，因此需要expand处理。expand(matrix(4*4*50),[2 2 1])/4    size为[8*8*50]
            end  
        elseif strcmp(net.layers{l}.type, 's')  
            for i = 1 : numel(net.layers{l}.a) % 第l层特征map的个数  
                z = zeros(size(net.layers{l}.a{1}));  
                for j = 1 : numel(net.layers{l + 1}.a) % 第l+1层特征map的个数  
                     z = z + convn(net.layers{l + 1}.d{j}, rot180(net.layers{l + 1}.k{i}{j}), 'full');  %下采样层f(x)=x,导数为1
                end  
                net.layers{l}.d{i} = z;  %得到下采样层的梯度
            end  
        end  
    end  
  
    %%  calc gradients  
    % 这里与 Notes on Convolutional Neural Networks 中不同，这里的 子采样 层没有参数，也没有  
    % 激活函数，所以在子采样层是没有需要求解的参数的  
    for l = 2 : n  
        if strcmp(net.layers{l}.type, 'c')  
            for j = 1 : numel(net.layers{l}.a)  
                for i = 1 : numel(net.layers{l - 1}.a)  
                    % dk 保存的是 误差对卷积核 的导数  
                    net.layers{l}.dk{i}{j} = convn(flipall(net.layers{l - 1}.a{i}), net.layers{l}.d{j}, 'valid') / size(net.layers{l}.d{j}, 3);  %除去batchsize，得到delta_W
                end  
                % db 保存的是 误差对于bias基 的导数  
                net.layers{l}.db{j} = sum(net.layers{l}.d{j}(:)) / size(net.layers{l}.d{j}, 3);  
            end  
        end  
    end  
    % 最后一层perceptron的gradient的计算  
    net.dffW = net.od * (net.fv)' / size(net.od, 2);  
    net.dffb = mean(net.od, 2);  
  
    function X = rot180(X)  
        X = flipdim(flipdim(X, 1), 2);  
    end  

    function X=flipall(X)
        for m=1:ndims(X)
            X=flipdim(X,m);
        end
    end

end  

sigm.m(修复之前运行提示找不到sigm函数的bug，把cnnbp.m中的sigm提出来，单独做一个m文件)

 function y=sigm(x)
         y=1./(1+exp(-x));
 end

 

cnnapplygrads.m

function net = cnnapplygrads(net, opts)  
    for l = 2 : numel(net.layers)  
        if strcmp(net.layers{l}.type, 'c')  
            for j = 1 : numel(net.layers{l}.a)  
                for ii = 1 : numel(net.layers{l - 1}.a)  
                    % 这里没什么好说的，就是普通的权值更新的公式：W_new = W_old - alpha * de/dW（误差对权值导数）  
                    net.layers{l}.k{ii}{j} = net.layers{l}.k{ii}{j} - opts.alpha * net.layers{l}.dk{ii}{j};  
                end  
            end  
            net.layers{l}.b{j} = net.layers{l}.b{j} - opts.alpha * net.layers{l}.db{j};  
        end  
    end  
  
    net.ffW = net.ffW - opts.alpha * net.dffW;  
    net.ffb = net.ffb - opts.alpha * net.dffb;  
end  

 

cnntest.m

function [er, bad] = cnntest(net, x, y)  
    %  feedforward  
    net = cnnff(net, x); % 前向传播得到输出  
    % [Y,I] = max(X) returns the indices of the maximum values in vector I  
    [~, h] = max(net.o); % 找到最大的输出对应的标签  
    [~, a] = max(y);     % 找到最大的期望输出对应的索引  
    bad = find(h ~= a);  % 找到他们不相同的个数，也就是错误的次数  
  
    er = numel(bad) / size(y, 2); % 计算错误率  
end  

使用我自己普通配置的笔记本进行的训练，每个epoch训练时间在3到4分钟。

训练结果为：

10000 test images0.01% error
60000 train images0.0016667% error

以上分析 若有错误之处，还希望大家帮忙指正。一起学习，共同进步。