Semi-supervised Domain Adaptation via Minimax Entropy

摘要

算法

整个网络分为两个部分：

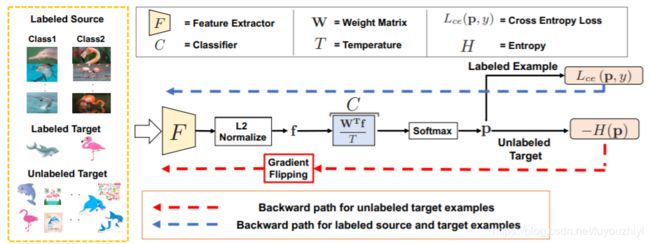
1. 特征提取器 F：采用主流的cnn网络，去掉最后的线性分类层
2. 分类器 C：k类别的线性分类器

图片x先输入到F中，得到F(x)。再计算l-2范数归一化后，得到$\frac{f(x)}{\Vert f(x)\Vert }$。 然后输入到分类器C中，得到 $\frac{1}{T}\frac{W^{T}f(x)}{\Vert f(x)\Vert }$。最后经过一个softmax层，输出
$$p(x)=\sigma (\frac{1}{T}\frac{W^{T}f(x)}{\Vert f(x)\Vert })$$

其中，分类器C的参数为 $W=[w_1,w_2,\cdots ,w_K]$（k为类别个数）。最终的输出可以写成
$$softmax\{\frac{1}{T}(w_1\frac{f(x)}{\Vert f(x)\Vert },w_2\frac{f(x)}{\Vert f(x)\Vert },\cdots ,w_K\frac{f(x)}{\Vert f(x)\Vert })\}$$
当$w_i$和$\frac{f(x)}{\Vert f(x)\Vert }$同方向时，这一项取最大值，此时类别为第$i$类
注：柯西不等式：
$$|(a,b)|\le |a|\cdot |b|$$

所以要想正确分类，权重向量$w_i$的方向必须和该类别特征的标准方向一致。所以论文视权重向量$w_i$为每个类别的估计原型

训练

首先用有标签的数据训练出一个模型来
$$\mathcal{L}={\mathbb{E}}_{(x,y)\in {\mathcal{D}}_s,{\mathcal{D}}_t}{\mathcal{L}}_{ce}(p(x),y)$$
本文利用最简单的交叉熵损失函数，训练源域和目标域中有标签的数据。但是这并不能保证模型能学到针对整个目标域的判别性特征。所以接下来要采用对抗的思想来训练无标记数据

本文有一个基本的假设是：
存在一个简单的域不变原型，能够代表两个域的所有数据

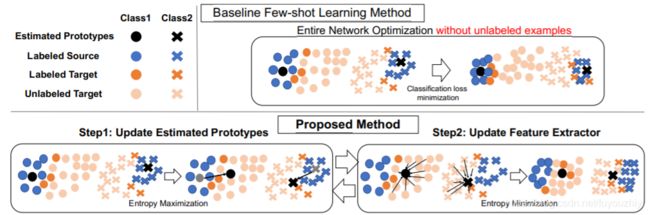
讲过上面交叉熵的loss后，原型$w_i$更靠近源域的分布，作者希望原型能向目标域偏移。所以针对目标域无标记数据计算香浓熵：
$$H=-{\mathbb{E}}_{(x,y)\in {\mathcal{D}}_u}\sum _{i=1}^{K}p(y=i|x)\log p(y=i|x)$$

增加熵值，则每个类输出的概率值很平均。此时，固定F，更新C的参数，能让原型$w_i$向未标记的目标域移动。

为了在未标记数据上学到判别性特征，训练F时，要减小熵值，使得未标记数据的特征聚集在估计原型周围

训练策略总结如下

看公式三，训练分两个步骤

1.固定分类器C，训练特征提取器F：利用有标记的数据训练模型提取到有用的特征。针对无标记的数据，最小化熵loss能提取到最具有判别性的特征。

关于熵loss的作用，这篇文章中有分析这里就不赘述了

https://www.toutiao.com/i6707098269777920516/

2.固定特征提取器F，训练分类器C：利用有标记的数据训练模型对特征进行正确分类。针对无标记的数据，最大化熵loss则会使

$$(w_1\frac{f(x)}{\Vert f(x)\Vert },w_2\frac{f(x)}{\Vert f(x)\Vert },\cdots ,w_K\frac{f(x)}{\Vert f(x)\Vert })$$
向量中的每一个分量都相似。这就迫使参数$w_i$向f(x)的方向靠近，也就是目标域未标记数据整体靠近。这样得到的原型$w_i$不仅包含了源域的信息还包含了目标域的信息。从而找到了域不变信息。

从这里我们也可以看出这篇论文的缺陷：$w_i$包含了有标记数据的第i类的信息，同时包含了目标域中所有无标记数据的信息。

我们期望$w_i$包含目标域中第i 类数据的信息，但是这并不好找到。