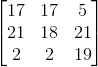密码学学习笔记 3.传统加密技术——代替技术（三）置换技术

Hill密码

用连续的m个密文字母取代原有的m个连续的明文，而且这m个密文是用m个线性方程来决定的。这里就用例子来演示。

首先我们先为26个字母进行定义，a=0,b=1,......,z=25。然后我们来看一下公式：

                                                            

                                                            

                                                            

整理得:

                                                       

所以可以看到： 加密： ；解密：

实例：

加密:i'm growing like a seed, rains been falling on me.

密钥：

先分组然后再加密，这里直接给出代码：

import re
import sys
in_text=sys.argv[1:]
P_E_S=['a','b','c','d','e','f','g','h','i','j','k','l','m','n','o','p','q','r','s','t','u','v','w','x','y','z']

Key=[[17,17,5],[21,18,21],[2,2,19]]
Key_I=[[4,9,15],[15,17,6],[24,0,17]]
def encryption(plaintex):
    ciphertext=[]
    flag=True
    while(flag):
        line=[]
        while(len(line)!=3):
            try:
                line.append(P_E_S.index(plaintex.pop(0))-P_E_S.index('a'))
            except:
                line.append(0)
                flag=False
        new_line=[]
        for i in range(3):
            new_line.append(0)
            for j in range(3):
                new_line[i]=new_line[i]+line[j]*Key[i][j]
        for i in range(3):
            ciphertext.append(P_E_S[new_line[i]%26])
    return ciphertext        
            

def decryption(ciphertext):
    plaintext=[]
    flag=True
    while(flag):
        line=[]
        while(len(line)!=3):
            try:
                line.append(P_E_S.index(ciphertext.pop(0))-P_E_S.index('a'))
            except:
                line.append(0)
                flag=False
        new_line=[]
        for i in range(3):
            new_line.append(0)
            for j in range(3):
                new_line[i]=new_line[i]+line[j]*Key_I[i][j]
        for i in range(3):
            plaintext.append(P_E_S[new_line[i]%26])
    return plaintext 
 


def Hill(in_text):
    print("此加密解密只涉及26个英文字母")
    print('---------------------------------')
    choice=input("1. 加密 2. 解密 ")
    in_text=''.join(in_text)
    in_text=re.compile('[^a-zA-Z]').sub('', in_text.lower())
    if choice is '1':
        print('加密结果: '+''.join(encryption(list(in_text))))
    elif choice is '2':
        print("解密结果: "+''.join(decryption(list(in_text))))
    else:
        print("输入错误")

        

if __name__ == '__main__':
    try:
        Hill(in_text)
    except EOFError:
        exit()

注：这个逆矩阵的求法，在后面的文章中会涉及，或者你可以尝试学习一下数论。

Hill密码的优势在于它屏蔽了单字母和双字母的频率特性，但是它很容易被已知明文攻击破解。

---

一次一密

两个基本难点：

1. 产生大规模随机密钥有困难。

2. 密钥的分配与保护有困难

---

置换技术

置换技术就是将原有的明文顺序进行打乱，通过多次的叠加，会增加破解的困难程度。

栅栏密码：

即设置分栏，然后将明文交叉存入，最后得到密码

实例： i'm growing like a seed, rains been falling on me. （栅栏为2）

栅栏1：i g o i g i e s e r i s e n a l n o m

栅栏2：m r w n l k a e d a n b e f l i g n e 

密文：igoigieserisenalnommrwnlkaedanbefligne

代码：

import re
import sys
from numpy import *
import numpy as np

in_text=sys.argv[1:]

def encryption(plaintex):
    ciphertext=[]
    c1=[]
    c2=[]
    i=0
    for item in plaintex:
        if i==0:
            c1.append(item)
            i+=1
        else:
            c2.append(item)
            i-=1
    ciphertext=c1+c2
    return ciphertext
            

def decryption(ciphertext):
    plaintext=[]
    length=len(ciphertext)
    cnt=0
    c1=[]
    c2=[]
    if length%2==0:
        for i in range(length//2):
            c1.append(ciphertext.pop(0))
        while(ciphertext):
            c2.append(ciphertext.pop(0))
    else:
        for i in range(length//2+1):
            c1.append(ciphertext.pop(0))
        while(ciphertext):
            c2.append(ciphertext.pop(0))
    cnt=0
    while(c1 or c2):
        if(cnt==0):
            plaintext.append(c1.pop(0))
            cnt+=1
        else:
            plaintext.append(c2.pop(0))
            cnt-=1
    return plaintext


def rail(in_text):
    print("此加密解密只涉及26个英文字母")
    print('---------------------------------')
    choice=input("1. 加密 2. 解密 ")
    in_text=''.join(in_text)
    in_text=re.compile('[^a-zA-Z]').sub('', in_text.lower())
    if choice is '1':
        print('加密结果: '+''.join(encryption(list(in_text))))
    elif choice is '2':
        print("解密结果: "+''.join(decryption(list(in_text))))
    else:
        print("输入错误")

        

if __name__ == '__main__':
    try:
        rail(in_text)
    except EOFError:
        exit()

如果只加密一次其实很容易就能发现结果了，那么多进行几次呢？比较一下

原文	i'm growing like a seed, rains been falling on me.
第一次	igoigieserisenalnommrwnlkaedanbefligne
第二次	iogeeieanmrnkeabfingiisrsnlomwladnelge
第三次	igeenrkafnisslmldegoeiamnebigirnowanle
第四次	ienkfismdgeanbgroalgeranslleoimeiinwne

这样的话解密难度就大大增加了。

---

转轮机 

转轮及就是将替代运算进行重复随机组合得到的结果。非常容易利用硬件实现。

我们来举个例子：

通过不同转速的密码盘，会随机生成不同的替代表，而且，每次都不是一样的。

---

 隐写术

这里仅仅举个例子，使用照片来存储一些重要的内容。我把一个简短的文字加入到了其中iloveyou

下面来看看，这两个文件有什么区别。

原图 更改后

 

---

博主还在学习密码学的相关内容，如有错误，还请各位指出，谢谢支持。