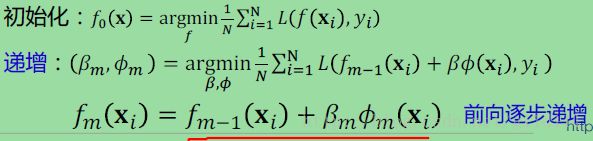XGBoost原理
前言
之前接触并实现过Adaboost和Random Forest。作为去年开始很火爆的，对结构化数据效果极佳的XGBoost，当然也需要了解一下了。下面将分段叙述XGBoost原理，以及与GBDT的关系等等内容。
①、XGBoost vs GBDT
说到XGBoost，不得不说GBDT，两者都是boosting方法。GBDT可以看成是Adaboost的前向逐步递增推导形式(——因为直接找到最优的模型 f f f是有难度的，所以采取每次递增的方式。)
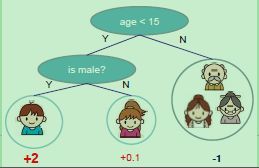
GBDT对分类问题基学习器是二叉分类树，对回归问题基学习器是二叉决策树。
N为样本个数。下面为训练第m个基学习器的过程。
-
损失函数： L ( f ( x ) , y ) L(f(x),y) L(f(x),y)
-
目标函数： m i n 1 N ∑ i = 1 N L ( f ( x i ) , y i ) min\frac {1}{N}\sum_{i=1}^{N}L(f(\mathbb x_i),y_i) minN1∑i=1NL(f(xi),yi)
-
前向算法：
-
指数损失对outliers比较敏感，而且，这种损失函数也不是二分类问题中的类别（label）取log后的表示。
-
因此另一种选择是负log似然损失，即得到logitBoost。此外，还可以取损失函数为L2损失，得到L2Boost。
为了便于推导，当采用平方误差损失函数时:
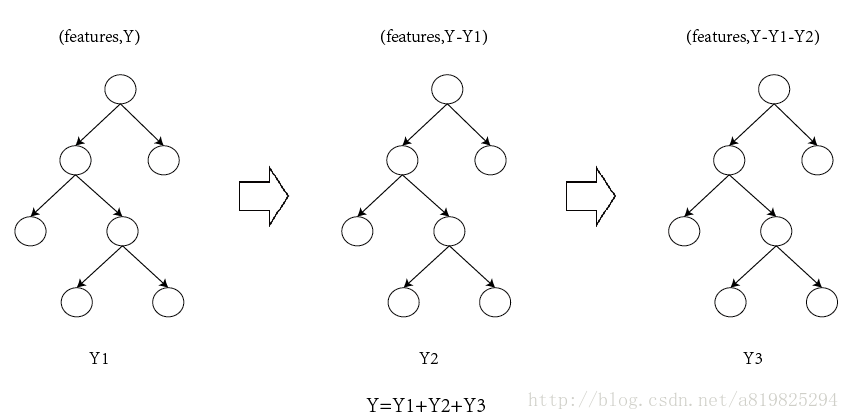
对于平方损失函数，拟合的就是残差；对于一般损失函数（梯度下降），拟合的就是残差的近似值。见下图（此图转自雪伦的博客）：
②、XGBoost推导
好了，说了半天GBDT，那什么是XGBoost呢？让我直接上图吧！哈哈
由于GBDT除了L2损失函数之外，对其它的损失函数推导比较复杂。而XGBoost采用对损失函数进行二阶Taylor展开来近似。简化了求解与推导。
由于函数在点x的泰勒展开形式为( n > = 3 n >= 3 n>=3)：
f ( x + Δ x ) ≃ f ( x ) + f ′ ( x ) Δ x + 1 2 ! f ′ ′ ( x ) Δ x 2 + o ( x ( n ) ) f(x+\Delta x) \simeq f(x) + f^{'}(x) \Delta x + \frac {1}{2!}f^{''}(x)\Delta x^2 + o(x^{(n)}) f(x+Δx)≃f(x)+f′(x)Δx+2!1f′′(x)Δx2+o(x(n))
ps: β \beta β 为1，所以 g m , i g_{m,i} gm,i后面的$\beta $可加可不加
树
- 树的定义：把树拆分成结构部分 q q q和叶子分数部分 w w w
- ϕ ( x ) = w q ( x ) , w ∈ R T , q ∈ R D → 1 , 2 , 3 , . . . , T \phi(x) = w_{q(\mathbf x)}, w \in \mathbf R^T, q \in \mathbf R^D \to {1,2,3,...,T} ϕ(x)=wq(x),w∈RT,q∈RD→1,2,3,...,T
- 结构函数 q q q：把输入映射到叶子的索引号
- 叶子分数函数 w w w：给出每个索引号对应的叶子的分数
- T为树中叶子结点的数目，D为特征维数
树的复杂度
树的复杂度定义为（不是唯一方式，不过下面的定义方式学习出的树效果一般都比较不错。）
其中， γ \gamma γ为 L 1 L1 L1正则的惩罚项， λ \lambda λ为 L 2 L2 L2正则的惩罚项。
目标函数
设目标函数为 J ( θ ) J(\theta) J(θ)
这一个目标函数中，包含了T个相互独立的单变量二次函数。我们可以定义：
G t = ∑ i ∈ I t g m , i G_t = \sum_{i \in I_t} g_{m,i} Gt=i∈It∑gm,i
H t = ∑ i ∈ I t h m , i H_t = \sum_{i \in I_t} h_{m,i} Ht=i∈It∑hm,i
将其代入上式中，得到简化的代价函数 J ( θ ) = ∑ t = 1 T [ G t w t + 1 2 ( H t + λ ) w t 2 ] + γ T J(\theta) = \sum_{t=1}^{T}[G_tw_t+\frac{1}{2}(H_t+\lambda)w_t^2]+\gamma T J(θ)=∑t=1T[Gtwt+21(Ht+λ)wt2]+γT
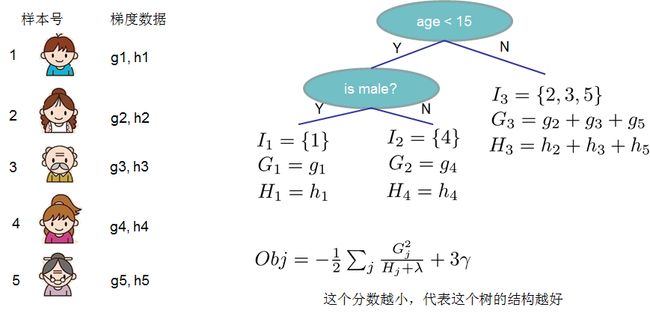
树的分数示例
O b j Obj Obj代表了当我们指定一个树的结构的时候，我们在目标函数上面最多减少多少。我们可以把它叫做结构分数(structure score)
③、建树（分裂节点）
- 枚举可能的树结构
- 计算结构分数
J ( θ ) = − 1 2 ∑ t = 1 T [ G t 2 H t + λ ] + γ T J(\theta) = -\frac {1} {2}\sum_{t=1}^{T}[\frac {G_t^2}{H_t + \lambda}]+\gamma T J(θ)=−21t=1∑T[Ht+λGt2]+γT - 选择分数最小树结构，并且运用最优的权重
- 但是，树结构有很多可能，所以对精确搜索的情况，可采用贪心算法。
(1) 贪心算法
实践中，我们贪婪的增加树的叶子结点数目:
（1）从深度为0的树开始
（2）对于树的每个叶子节点，尝试增加一个分裂点：
对于每次扩展，我们还是要穷举所有可能的分割方案
一、 对每个特征，通过特征值将实例进行排序
二、 运用线性扫描来寻找该特征的最优分裂点
三、 对所有特征，采用最佳分裂点
如何高效地枚举所有的分割呢？我假设我们要枚举所有x < a 这样的条件，对于某个特定的分割a我们要计算a左边和右边的导数和。
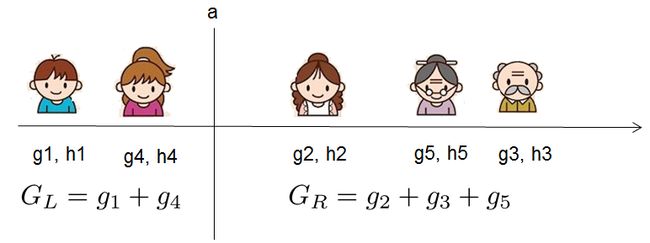
我们可以发现对于所有的a，我们只要做一遍从左到右的扫描就可以枚举出所有分割的梯度和 G L G_L GL和 G R G_R GR。然后用上面的公式计算每个分割方案的分数就可以了。
• 深度为k的树的时间复杂度：
– 对于一层排序，需要时间Nlog(N)，N为样本数目
– 对有D个特征，k层的二叉树，有复杂度为kDNlog(N)
伪代码如下：
(2) 近似搜索算法
算法产生原因：当数据太多不能装载到内存时，不能进行精确搜索分裂，只能近似。
根据特征分布的百分位数，提出特征的一些候选分裂点
将连续特征值映射到桶里（候选点对应的分裂），然后根据桶里
样本的统计量，从这些候选中选择最佳分裂点
根据候选提出的时间，分为:
全局近似：在构造树的初始阶段提出所有的候选分裂点，然后对下面的各个层次采用相同的候选特征分裂点。
特点：提出候选的次数少，但每次的候选数目多（因为候选不更新）
局部近似：在每次分裂都重新提出候选特征分裂点。
特点：对层次较深的树更适合
伪代码如下：
之后还会补充的更全一些。。
参考资料：
1、雪伦的博客
2、冒老师的XGBoost课程
3、xgboost导读和实战
4、Tianqi Chen 的论文：XGBoost: Reliable Large-scale Tree Boosting System