神经网络前向后向传播推导及实现
本文主要是BP网络的前后向传播较详细推导,以及C++实现,记下来也方便后面的回顾,也希望对关系细节的读者也一丝帮助。如果有不对的地方,请指正。
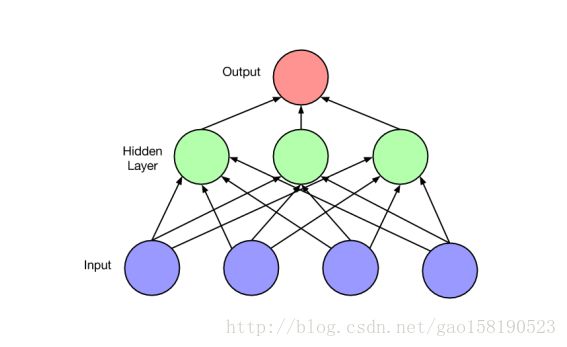
BP图模型:
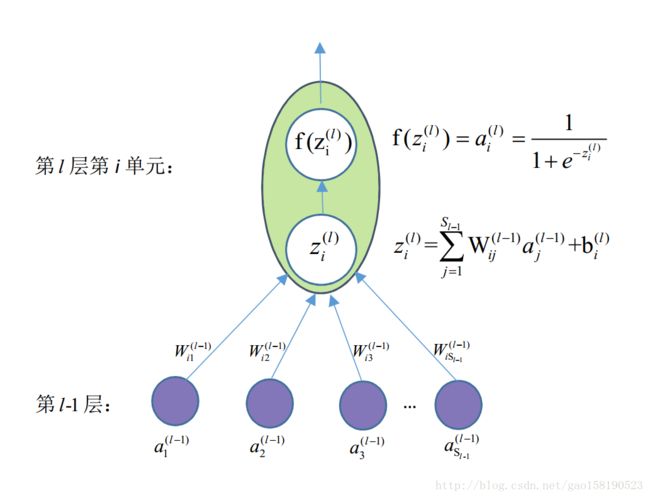
网络中单个激活单元:
- 上图定了隐层中的激活单元,该隐层激活单元中含有一个偏置项b。相关运算如图所示,符号右上角角标为单元在网络中的层好,结合代码实现时,网络激活单元之间的权重一般保存在前一层的单元中。
这里有两点注意:
- 输入层的单元中没有偏置项b,但有权值项w。
- 输出层的单元中没有权值项w,但有偏置项b。
相关符号定义:
| 符号 | 意义 |
|---|---|
| m | 样本数 |
| nl | 网络的总层数 |
| Ll | 第 l 层 |
| W(l)ij | l 层的j单元与 l+1 的i单元之间的权值(weight) |
| b(l)i | 第 l 层第i个单元的偏置项 |
| Sl | 表示第 l 层的节点数 |
| a(l)i | 表示第 l 层第i单元的激活值 |
| f(x) | sigmoid函数: f(x)=11+e−x |
| z(l)i | 表示第 l 层第i单元的输入 |
| hwb(x) | 表示整个网络对输入x的输出结果,等价于 a(nl) |
损失函数(带2范式正则):
J(W,b)=1m∑i=1mJ(W,b;xi,yi)+λ2∑l=1nl−1∑i=1Sl∑j=1Sl+1(W(l)ji)2
其中,J(W,b;x,y)=12∥hwb(x)−y∥2
我们优化所有权值和偏置就是通过最小化损失函数来实现的,通过对损失函数计算各权值和偏置的梯度,然后沿着各自梯度的反方向走,就可以让损失函数慢慢变小,由于神经网络不是的损失函数不是严格凸函数,所以并不能保证找到全局最优解。我们首先就要计算各权值和偏置关于损失函数的梯度。
前向传播
Tip : 这里需要先初始化各单元中的权值和偏置项的值,权值可以按照标准正态分布去产生,也可以使用其它方式产生,但最好不要偷懒而给所有权值赋上相同的值,这样会导致极慢的收敛速度,有兴趣的读者可以修改下面的程序自己试下。
- 输入层向隐层的前向传播:
- 向输入层输入数据X,第二层第i个激活单元相关计算:
该激活单元的输入: z(2)i=∑j=1S1W(1)ija(1)j+b(2)i ,其中 a(1)i=Xi
该激活单元的输入: a(2)i=f(z(2)i)=11+e−z(2)i
计算完输入层的前向传播后就可以计算隐层间的传播了。
- 向输入层输入数据X,第二层第i个激活单元相关计算:
- 隐层间的传播:
- 上一层的隐层输出值作为当前隐层的输入值:
第l 层第i个激活单元输入: z(l)i=∑j=1Sl−1W(l−1)ija(l−1)j+b(l)i
第l 层第i个激活单元输出: a(l)i=f(z(l)i)=11+e−z(l)i
隐层按照从低向高的顺序依次计算各层的激活单元,依次计算各层: l=3,4,...Snl−1
- 上一层的隐层输出值作为当前隐层的输入值:
- 输出层的传播:
- 传播到最后的输出层:
第 Snl 层第i个激活单元输入: z(nl)i=∑j=1Snl−1W(nl−1)ija(nl−1)j+b(nl)i
第 Snl 层第i个激活单元最终的输出: a(nl)i=f(z(nl)i)=11+e−z(nl)i
其中 a(nl)i 就是神经网络最终的输出。
- 传播到最后的输出层:
反向传播
Tip : 如果直接对损失函数中位于第一层的权值求导,会发现无从下手,因为后面的所有层的激活单元都直接或间接的包含了第一层的权值,这是一种嵌套的关系(数学函数嵌套,类似于斐波那契数列),第一层的权值被嵌套的最深。换言之,约靠后的激活单元,其权值在损失函数中嵌套的就越浅。既然这样,那我们可以先从靠后的权值下手,比如倒数第二层的权值 Wnl−1 ,在损失函数中,就是最顶层的(输出层没有权值)。为了后期计算的方便,我们从后向前对各层各激活单元的输入变量 Zli 求导。后在对 Wli 求导就显得非常简单了,这里主要是求导的链式法则起到了关键作用(题外话:RNN中的LSTM单元也是通过这种思想求解,可以将时间t比作层数来从后向前计算)。
- 反向传播之输出层:
δnli=∂J(W,b;x,y)∂Znli=∂12∥hwb(x)−y∥2∂Znli=∂12∥∥anli−y∥∥2∂Znli=∂12∥∥f(Znli)−y∥∥2∂Znli=(anli−yi)∂f(Znli)∂Znli=(anli−yi)f(Znli)(1−f(Znli)) - 反向传播之隐藏层和输入层:
这里假设我们已经将后一层的 δl+1i 计算出来了(实际上输出层(最后一层)上的 δnli 已经根据上面的公式计算出来了),下面计算来计算 δli :
计算各权值和偏置的梯度:
更新策略:对于每一个样本 (xi,yi) ,先使用前向传播计算出各激活单元的输出值 ali ,再通过反向传播,计算出各激活单元的输入关于单个样本对应损失函数的偏导 δli ,之后就可以是用下面的公式对所有样本求出每个权值和偏置的偏导,并使用优化算法对其更新,这里使用的是梯度下降,也可以使用SGD等优化算法。
权值关于损失函数的梯度:
∂J(W,b)∂W(l)ji=1m∑t=1m∂J(W,b;xt,yt)∂W(l)ji+λW(l)ji=1m∑t=1m⎛⎝∂J(W,b;xt,yt)∂Zl+1j×∂Zl+1j∂W(l)ji⎞⎠+λW(l)ji=1m∑t=1m⎛⎝δl+1j×∂Zl+1j∂W(l)ji⎞⎠+λW(l)ji=1m∑t=1m⎛⎝⎜⎜⎜⎜⎜δl+1j×∂(∑k=1Sl(Wljkalk)+bli)∂W(l)ji⎞⎠⎟⎟⎟⎟⎟+λW(l)ji=1m∑t=1m(δl+1j×ali)+λW(l)ji偏置关于损失函数的梯度:
程序中相关变量解释:
| 变量名 | 代表含义 |
|---|---|
| value | 对应单元的激活值: a(l)i |
| rightout | 样本真实值: yi |
| error | 损失误差: 1m∑i=1mJ(W,b;xi,yi) |
| delta | 单个样本偏差: ∂J(W,b;xi,yi)∂W(l)ji |
| wDeltaSum | 整个样本偏差和,即最终的权值偏差: ∂J(W,b)∂W(l)ji |
下面是c++版实现程序(没有使用正则):
- 注:程序实现的是对XOR运算的拟合
BpNet.h:
#includeBpNet.cpp:
#include "BpNet.h"
using namespace std;
BpNet::BpNet()
{
srand((unsigned)time(NULL));
error = 100.f;
//初始化输入层
for(int i = 0; i< innode; i++)
{
inputLayer[i] = new inputNode();
for(int j = 0; j < hidenode; j++)
{
inputLayer[i]->weight.push_back(get_11Random());
inputLayer[i]->wDeltaSum.push_back(0.f);
}
}
//初始化隐藏层
for ( int i = 0; i < hidelayer; i++)
{
if ( i ==hidelayer - 1)
{
for(int j = 0;j < hidenode; j++ )
{
hiddenLayer[i][j] = new hiddenNode();
hiddenLayer[i][j]->bias = get_11Random();
for (int k = 0;k < outnode; k++)
{
hiddenLayer[i][j]->weight.push_back(get_11Random());
hiddenLayer[i][j]->wDeltaSum.push_back(0.f);
}
}
}
else
{
for (int j =0; j < hidenode; j++)
{
hiddenLayer[i][j] = new hiddenNode();
hiddenLayer[i][j]->bias = get_11Random();
for (int k = 0; k < hidenode; k++)
{
hiddenLayer[i][j]->weight.push_back(get_11Random());
hiddenLayer[i][j]->wDeltaSum.push_back(0.f);
}
}
}
}
//初始化输出层
for ( int i = 0; i < outnode; i++)
{
outputLayer[i] = new outputNode();
outputLayer[i]->bias = get_11Random();
}
}
void BpNet::forwardPropagationEpoc()
{
//forward propagation on hidden layer
for ( int i = 0; i < hidelayer; i++)
{
if (i == 0 )
{
for ( int j = 0; j < hidenode; j++)
{
double sum = 0.f;
for ( int k = 0; k < innode; k++)
{
sum += inputLayer[k]->value * inputLayer[k]->weight[j];
}
sum += hiddenLayer[i][j]->bias;
hiddenLayer[i][j]->value = sigmoid(sum);
}
}
else
{
for ( int j = 0; j < hidenode; j++)
{
double sum = 0.f;
for ( int k = 0; k < hidenode; k++)
{
sum += hiddenLayer[i-1][k]->value*hiddenLayer[i-1][k]->weight[j];
}
sum += hiddenLayer[i][j]->bias;
hiddenLayer[i][j]->value = sigmoid(sum);
}
}
}
//forward propagation on output layer
for ( int i = 0; i < outnode; i++)
{
double sum = 0.f;
for( int j = 0; j < hidenode; j++)
{
sum += hiddenLayer[hidelayer - 1][j]->value * hiddenLayer[hidelayer - 1][j]->weight[i];
}
sum += outputLayer[i]->bias;
outputLayer[i]->value = sigmoid(sum);
}
}
void BpNet::backPropagationEpoc()
{
// backward propagation on output layer
// -- comput delta
for ( int i = 0; i < outnode; i++)
{
double temp = fabs(outputLayer[i]->value-outputLayer[i]->rightout);
error += temp * temp / 2;
outputLayer[i]->delta = (outputLayer[i]->value - outputLayer[i]->rightout)*(1-outputLayer[i]->value)*outputLayer[i]->value;
}
// backward propagation on hidden layer
// compute delta
for ( int i = hidelayer - 1; i >= 0; i--)
{
if ( i == hidelayer - 1)
{
for ( int j = 0; j < hidenode; j++)
{
double sum = 0.f;
for ( int k = 0; k < outnode; k++)
{
sum += outputLayer[k]->delta * hiddenLayer[i][j]->weight[k];
}
hiddenLayer[i][j]->delta = sum*hiddenLayer[i][j]->value*(1 - hiddenLayer[i][j]->value);
}
}
else
{
for ( int j = 0; j < hidenode; j++)
{
double sum = 0.f;
for ( int k = 0; k < hidenode; k++)
{
sum += hiddenLayer[i + 1][k]->delta * hiddenLayer[i][j]->weight[k];
}
hiddenLayer[i][j]->delta = sum * hiddenLayer[i][j]->value*(1-hiddenLayer[i][j]->value);
}
}
}
// backward propagation on input layer
// update weight delta sum
for ( int i = 0; i < innode; i++)
{
for ( int j = 0; j < hidenode; j++)
{
inputLayer[i]->wDeltaSum[j] += inputLayer[i]->value*hiddenLayer[0][j]->delta;
}
}
// backward propagation on hidden layer
// update weight delta sum and bias delta sum
// 计算偏导数
for ( int i = 0; i < hidelayer; i++)
{
if ( i == hidelayer - 1)
{
for ( int j = 0; j < hidenode; j++)
{
hiddenLayer[i][j]->bDeltaSum += hiddenLayer[i][j]->delta;
for ( int k = 0; k < outnode; k++)
{
hiddenLayer[i][j]->wDeltaSum[k] += hiddenLayer[i][j]->value * outputLayer[k]->delta;
}
}
}
else
{
for (int j = 0; j < hidenode; j++)
{
hiddenLayer[i][j]->bDeltaSum += hiddenLayer[i][j]->delta;
for ( int k = 0; k < hidenode; k++)
{
hiddenLayer[i][j]->wDeltaSum[k] += hiddenLayer[i][j]->value * hiddenLayer[i+1][k]->delta;
}
}
}
}
// backward propagation on output layer
// update bias delta sum
for ( int i = 0; i < outnode; i++)
{
outputLayer[i]->bDeltaSum += outputLayer[i]->delta;
}
}
void BpNet::training(static vector0.f;
//initialize delta sum
for ( int i = 0; i < innode; i++)
{
inputLayer[i]->wDeltaSum.assign(inputLayer[i]->wDeltaSum.size(), 0.f);
}
for ( int i = 0; i < hidelayer; i++)
{
for ( int j = 0; j < hidenode; j++)
{
hiddenLayer[i][j]->wDeltaSum.assign(hiddenLayer[i][j]->wDeltaSum.size(), 0.f);
hiddenLayer[i][j]->bDeltaSum = 0.f;
}
}
for ( int i = 0; i < outnode; i++)
{
outputLayer[i]->bDeltaSum = 0.f;
}
// start training
for( int iter = 0; iter < sampleNum; iter++)
{
// initial data of input and output
setInput(sampleGroup[iter].in);
setOutput(sampleGroup[iter].out);
// forward and backward propagation
// compute delta
forwardPropagationEpoc();
backPropagationEpoc();
}
// deltasum had computed over! then update weight and bias
// backward propagation on input layer
// update weight with Gradient descent
for ( int i = 0; i < innode; i++)
{
for ( int j = 0; j < hidenode; j++)
{
inputLayer[i]->weight[j] -= learningRate * inputLayer[i]->wDeltaSum[j] /sampleNum;
}
}
// backward propagation on hidden layer
// update weight and bias
for ( int i = 0; i < hidelayer; i++)
{
if( i == hidelayer -1)
{
for ( int j = 0; j < hidenode; j++)
{
// update bias
hiddenLayer[i][j]->bias -= learningRate * hiddenLayer[i][j]->bDeltaSum/sampleNum;
// update weight
for ( int k = 0; k < outnode; k++)
{
hiddenLayer[i][j]->weight[k] -= learningRate * hiddenLayer[i][j]->wDeltaSum[k]/sampleNum;
}
}
}
else
{
for ( int j = 0; j < hidenode; j++)
{
// update bias
hiddenLayer[i][j]->bias -= learningRate * hiddenLayer[i][j]->bDeltaSum/sampleNum;
// update weight
for ( int k = 0; k < hidenode; k++)
{
hiddenLayer[i][j]->weight[k] -= learningRate * hiddenLayer[i][j]->wDeltaSum[k]/sampleNum;
}
}
}
}
// backward propagation on output layer
// udate bias
for ( int i = 0; i < outnode; i++)
{
outputLayer[i]->bias -= learningRate * outputLayer[i]->bDeltaSum/sampleNum;
}
}
}
void BpNet::predict(vector 本文为作者原创,转载请注明出处,谢谢!
参考
- A Critical Review of Recurrent Neural Networks for Sequence Learning
- Supervised Sequence Labelling with Recurrent Neural Networks
- http://deeplearning.stanford.edu/wiki/index.php/%E5%8F%8D%E5%90%91%E4%BC%A0%E5%AF%BC%E7%AE%97%E6%B3%95
- http://blog.csdn.net/ironyoung/article/details/49455343