深度置信网络（一）：HopField网络

HopField

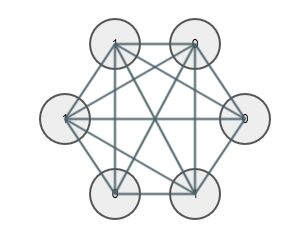
这里我们分析离散型的HopField网络。HopFiled网络由循环相连的二值神经元组成，如下图:

图1：

• 图中每两个神经元间的连接都是双向的
• 每个节点 i i 都有一个二值状态值 si s i ，取值为0、1或则1、-1；所有神经元的状态值组合，称为HopField网络的一个组态（configuration）
• 每个节点 i i 都有一个偏移值 bi b i .

一般来说，这种循环神经网络是比较难以分析的，它们的行为一般会分为三类：

• 收敛到一个稳定的状态
• 在几个稳定状态之间不断的震荡
• 混沌状态

但是John Hopfield发现，对于网络的每一个组态都有一个对应的能量值，每个神经元遵循一定的状态更新规则，可以使网络的能量降到最低。

例如，我们可以这样来定义网络的能量：

E=−∑isibi−∑i<jsisjwij E = − ∑ i s i b i − ∑ i < j s i s j w i j

在这个能量定义下，我们可以计算每个神经元在在两个不同状态下网络整体能量的差异:

Energy gap=ΔEi=E(si=0)−E(si=1)=bi+∑jsjwij E n e r g y   g a p = Δ E i = E ( s i = 0 ) − E ( s i = 1 ) = b i + ∑ j s j w i j

为了使网络的能量降到最低，我们设计这样一个更新规则：

• 1、每个神经元的状态从随机值开始
• 2、每次更新一个神经元的状态值，使得网络的整体能量值降低，也就是说 ΔEi>0, Δ E i > 0 , 则更新状态值 si=1 s i = 1 ,否则 si=0 s i = 0
• 3、不断执行第2步，直到没有神经元的状态改变为止，此时网络的能量值达到最低。

实际上，HopField网络在我们设计的状态更新规则下，总是会朝着能量降低的方向变化，最终收敛到一个稳定的组态（configuration），不再变化，这个组态也是能量的最低点。这个组态称为HopField网络的吸引子。事实上，一个HopField网络可能有多个吸引子，取决于网络中连接的权重和神经元的偏移值；最终收敛到哪一个吸引子，则取决于网络初始的组态。

那么，HopField的这个特征有什么应用呢？

1982年，HopField提出可以利用网络能量最低点的网络组态来存储数据。这个说法有点抽象，具体来说也就是，我们可以通过一定非方式调整网络的结构和网络中权重的取值，使网络的吸引子恰好是我们想要存储的数据。

举个例子，比如我们想要存储数字1和2的图片：

我们可以设计这样一个hopfield网络，图片的每个像素对应网络中一个神经元，然后我们通过一定非方式方式（其实就是后面将要介绍的HopField网络的学习算法），调整网络中权重值，使得网络有两个吸引子，分别对应这两张图片。也就是说，我们的网络就”学习并记住了”这两张图片。

那么，上面训练完的HopField网络又有什么用处呢？

实际上我们可以用这个HopField网络来做图像识别。在实际的图像识别任务中，我们采集到的待识别的数据可能是不完整的，模糊不清晰的，例如：

将这些损坏的数据作为上面训练完的HopField网络的初始组态，然后按照HopField网络的状态更新规则，最终我们的网络会收敛到与初始状态最接近的吸引子状态，这个吸引子状态就是真实的数据。

HopField网络的训练

HopField网络的训练过程实际上就是使一些组态称为网络能量的最低点，也就是在核定状态s的情况下，最小化能量函数：

E=−∑isibi−∑i<jsisjwij E = − ∑ i s i b i − ∑ i < j s i s j w i j

根据Hebian学习规则，如果神经元的状态值取1或-1，则参数的更新规则：

wij→wij+sisj w i j → w i j + s i s j

bi→bi+si b i → b i + s i

如果神经元的状态值取0或1，则参数的更新规则：

wij→wij+4(si−12)(sj−12) w i j → w i j + 4 ( s i − 1 2 ) ( s j − 1 2 )

bi→bi+si−12 b i → b i + s i − 1 2

另外，在网络规模较小的情况下，也可以直接使用联立不等式的方式求解，因为网络中神经元的状态取决于 Energy gap E n e r g y   g a p ，所以比如需要一个特定的神经元取状态值1，则得到不等式 Energy gap>0 E n e r g y   g a p > 0 , 取值为0，则得到不等式 Energy gap<0 E n e r g y   g a p < 0 ，这样就可以通过求解这些不等式来求得网络的参数。

带隐藏层的HopField网络

HopField网络除了可以用于存储数据以外，还可以用与”解释”数据：

• 神经元分为可视神经元和隐藏神经元
• 可视神经元的状态表示输入数据
• 隐藏神经元的状态表示输入数据的一个”解释”
• “解释”的好坏取决于网络的能量，能量越低，”解释”越合理。

但是，这个”解释模型”存在两个问题：

• 连接可视神经元与隐藏神经元的权重以及隐藏神经元之间的权重怎么训练？
• 怎么才能避免陷入能量的局部最低值，达到能量的全局最低值？

进一步的分析将引入的下一章的主题：玻尔兹曼机。