OpenGL ES之九——相机和投影

概述

这是一个系列的Android平台下OpenGl ES介绍，从最基本的使用最终到VR图的展示的实现，属于基础篇。（后面针对VR视频会再有几篇文章，属于进阶篇）

OpenGL ES之一——概念扫盲
OpenGL ES之二——Android中的OpenGL ES概述
OpenGL ES之三——绘制纯色背景
OpenGL ES之四——绘制点，线，三角形
OpenGL ES之五——相机和投影，绘制等腰三角形
OpenGL ES之六——绘制矩形和圆形
OpenGL ES之七——着色器语言GLSL
OpenGL ES之八——GLES20类和Matrix类
OpenGL ES之九——相机和投影
OpenGL ES之十——纹理贴图（展示一张图片）
OpenGL ES之十一——绘制3D图形
OpenGL ES之十二——地球仪和VR图

本篇概述

前面一直在使用相机矩阵和投影矩阵来解决平面图形变形的问题，但是其中的原理一直没有阐述，其实是怕不结合实例很难解释的清楚。现在水到渠成了，接触了很多使用OpenGLES绘制2D图形，想必都有了一些感觉，接下来可以好好解释一下了。

一.OpenGL的世界

这里不会将官网上概念搬过来，而是将各种概念以容易理解的方式阐述。

1. 相机就相当于我们的眼睛；
2. 人类的视野范围是有限的，所以就有了“视景体”或者叫“裁剪体”；
3. 物体反射光或者发光投射到“指定的屏幕上”，这就是投影；

变换矩阵

我们在之前绘制点，线，三角形的时候发现即使我们给的坐标是构成等腰三角形的坐标，最终绘制的结果也不是。后来我们使用了变换矩阵将我们本想绘制的等腰直角三角形绘制了出来，而它的出处如下（之前阐述过OpenGl的2D坐标系和屏幕坐标系的关系所以这里不做赘述）：
先给出顶点位置变换公式
其中从左往右各个参数解释如下：

第一个：变换结果；
第二个：投影矩阵；
第三个：相机矩阵；
第四个：模型矩阵；
第五个：顶点位置参数所在的向量。

我们之前使用的时候将投影矩阵和相机矩阵相乘为变换矩阵使用。而这里的模型矩阵我们可以理解为一个单位矩阵（我们习惯将2D平面设置为x和y轴组成的平面，而z轴作为垂直于该平面的方向）。

二 投影

2.1 视景体

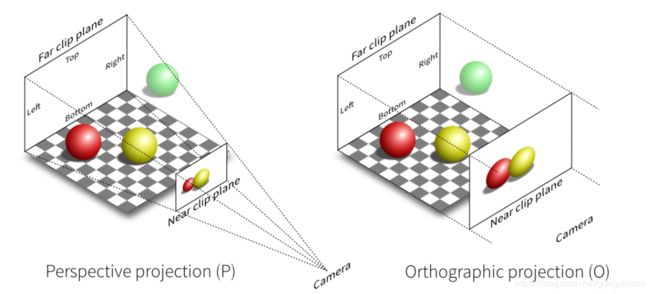
先看下图

上图中六个平面围成的空间就是“视景体”或者称为“裁剪空间”，只有被观察的物体在其中我们才能看得见。同时注意这里的远，近平面是以相机为基准的。同时图像是呈现在近平面上的。

2.2 透视投影和正交投影

先看图：

从图中我们可以很容易看出区别：

透视投影：相机看作一个点，由相机发出的视线与视景体远平面构成椎体。
正交投影：相机看作和近，远平面大小相同并平行的矩形，由相机发出的视线与视景体远平面构成长方体。
最终图像都投影到近平面上。

然后看我们获取投影矩阵的方法

透视投影

public static void frustumM(float[] m, int offset,
				            float left, float right,
				            float bottom, float top,
				            float near, float far)

正交投影

public static void orthoM(float[] m, int mOffset,
					        float left, float right, 
					        float bottom, float top,
					        float near, float far) 

两个方法的参数：m指的是装载结果矩阵的数组；offset指矩阵偏移量；其他在图中标记的很明显了，这里不做赘述。

2.3 参数的传递规则

之前解决三角形的拉伸问题我们使用如下：

		//相机和透视投影方式
        //计算宽高比
        float ratio=(float)width/height;
        //设置透视投影
        Matrix.frustumM(mProjectMatrix, 0, -ratio, ratio, -1, 1, 3, 7);
        //设置相机位置
        Matrix.setLookAtM(mViewMatrix, 0, 0, 0, 7.0f, 0f, 0f, 0f, 0f, 1.0f, 0.0f);
        //计算变换矩阵
        Matrix.multiplyMM(mMVPMatrix,0,mProjectMatrix,0,mViewMatrix,0);


        /*//正交投影方式
        final float aspectRatio = width > height ?
                (float) width / (float) height :
                (float) height / (float) width;
        if (width > height) {
            //横屏
            Matrix.orthoM(mMVPMatrix, 0, -aspectRatio, aspectRatio, -1f, 1f, -1f, 1f);
        } else {
            //竖屏
            Matrix.orthoM(mMVPMatrix, 0, -1f, 1f, -aspectRatio, aspectRatio, -1f, 1f);
        }*/

不管是正交投影还是透视投影，最终都是将视景体内的物体投影在近平面上，这也是 3D 坐标转换到 2D 坐标的关键一步。
而近平面上的坐标接着也会转换成归一化设备坐标，再映射到屏幕视口上。
为了解决之前的图像拉伸问题，就是要保证近平面的宽高比和视口的宽高比一致，而且是以较短的那一边作为 1 的标准，让图像保持居中。

2.4 另一种获取透视投影的方法perspectiveM

如下：

public static void perspectiveM(float[] m, int offset,
          float fovy, float aspect, float zNear, float zFar) 

看下图，帮助理解

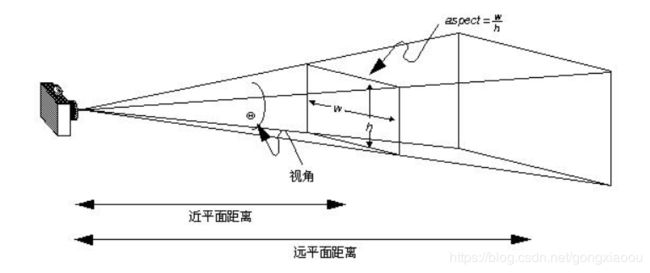
perspectiveM 函数来创建投影矩阵，它的视景体和 frustumM 函数相同，但是构造的参数有所不同。
视景体不再需要确定近平面左、上、右、下距离了。
通过视角来决定我们能看到的视野大小。视角就是图中所示的那个夹角。另外的参数是视口的宽高比，还有近平面和远平面的距离，参数个数减少了。
如下图：

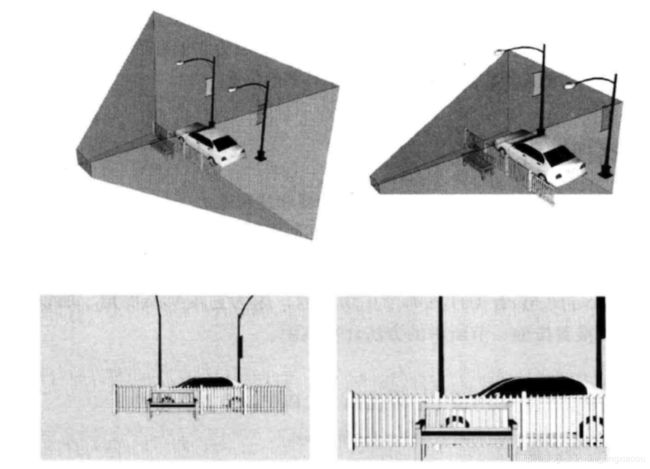
上述图片左边是 90 视角，右边是 45 度视角。显然，视野角度越大，则看到的内容更多，但是物体显得更小，而视野角度越小，则看的内容更少，但物体显得更大。

和 frustumM不同的是，一旦确定了视角和宽高比，那么整个摄像机视野也就确定了，此时完整的锥形视野已经形成了，也就是说物体的近大远小效果已经完成了。这时，近平面距离和远平面距离只是确定想要截取锥形视野中的哪一部分了。不像在frustumM函数中，近、远平面的距离还能够调整近大远小的效果。

三 相机

先看图

这里的相机模拟了真实环境中相机。OpenGL 本身是没有相机的概念的，不过为了营造出运动的效果，我们可以移动相机产生相对运动（例如平移，转动等）。
我们通过下面的方法来设置相机的各个参数：

Matrix.setLookAtM(float[] rm, int rmOffset,
		            float eyeX, float eyeY, float eyeZ,
		            float centerX, float centerY, float centerZ,
		             float upX, float upY, float upZ) 

上面参数的解释：

第一行中：rm：装有结果的投影矩阵；rmOffset：投影矩阵偏移量
第二行：指定相机的位置；
第三行：指定被观察物的位置：（相机位置点指向被观察物位置点，组成一个向量，这个就是相机的拍摄方向）
第四行：相机上方向。（我们可以想象成原始相机上面那个闪光灯的朝向）