自己用java实现二叉树的增，删，查

在看TreeMap的源码之前，有必要先了解下tree这个数据结构，很早之前看java版的数据结构与算法，也是卡到tree这里，没再读下去。现在重新复习这块知识。先从二叉树开始吧，BST 英文 binary search tree 直译二分查找树。

某个节点的值都大于该节点的左子树里所有的节点。反之右子树的所有节点的值都大于该节点。

记忆 ： 大佐（左）

节点 有父类节点，左子树节点，右子树节点，实现了Comparable的value

static class Node implements Comparable{
		Node parent;//父类节点
		Node left;//左子树节点
		Node right;//右子树节点
		Comparable value;//实现了Comparable的value 
		public Node(Node parent, Comparable value, Node left, Node right){
			this.parent=parent;
			this.left=left;
			this.right=right;
			this.value=value;
		}
}

它的操作主要有

a.插入

b.遍历

假设如下

遍历又分为

1.深度优先： 沿着树的深度遍历树的节点，尽可能深的搜索树的分支,

深度优先遍历又分为前序遍历，中序遍历，后序遍历

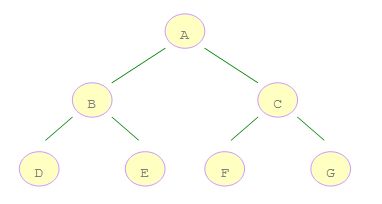
上面二叉树的前序遍历 顺序为：ABDECFG

上面二叉树的中序遍历 顺序为：DBEAFCG

上面二叉树的后序遍历 顺序为：DEBFGCA

根节点在哪个位置输出就是什么顺序遍历

2.广度优先 : 从根结点开始沿着树的宽度搜索遍历，

上面二叉树的遍历顺序为：ABCDEFG

c.删除

1.删除的节点只有右子树,只要把节点的父节点的右子树指向删除节点的右子树

eg:删除52后， 50.right(52.parent)--->54(52.right)

2.删除的节点只有左子树,只要把节点的父节点的左子树指向删除节点的左子树

eg:删除83后，85.left(83.parent)--->54(83.left)

3.删除的节点有右子树和左子树。有2种算法

从删除的节点的左子树里找到最大的值,作为删除节点的父节点的左或右子树（依据于删除节点原来是父节点的左或右）

eg:删除35后，68.left(35.parent)--->33

从删除的节点的右子树里找到最小的值，作为删除节点的父节点的左或右子树（依据于删除节点原来是父节点的左或右）

eg:删除35后，68.left(35.parent)--->50，删掉50后，后续52接上

纸上得来终觉浅，绝知此事要躬行。接下来就是撸代码了，主要是理解原理的基础上来写就不会觉得很难。

1.定义一个类MyBST

里面有static class Node。是不是和hashmap里的HashMap.Node一样，

这是读源码的一个好处吧。

public class MyBST>  {
static class Node implements Comparable,Cloneable{
		Node parent;//父类节点
		Node left;//左子树节点
		Node right;//右子树节点
		Comparable value;//实现了Comparable的value 
		public Node(Node parent, Comparable value, Node left, Node right){
			this.parent=parent;
			this.left=left;
			this.right=right;
			this.value=value;
		}
}
}

2.增加

增加的代码不是很难写

public boolean add(C c){
		if(root==null){
			root = new MyBST.Node(null,c,null,null);			
		}else{
			Node node = root;
			Node nodeParent = root;
			boolean isNodeLeft = false;
 //按大左小右,直到node为空,nodeParent 就是要插入的父节点了，
 //注意isNodeLeft来判断到底是插入nodeParent.right还是nodeParent.left
			while(node!=null){
				nodeParent = node;
				if(node.value.compareTo(c)>0){
					//should put root.left
					node=node.left;
					isNodeLeft = true;
				}else if(node.value.compareTo(c)<0){
					//should put root.right
					node=node.right;
					isNodeLeft = false;
				}else{
					System.out.println("can‘t add duplicate value");
					return false;
				}				
			}
			node = new MyBST.Node(nodeParent,c,null,null);
			if(isNodeLeft)
				nodeParent.left = node;
			else
				nodeParent.right = node;			
		}
		return true;
	}

3.遍历

只写了深度优先的前序遍历，中序遍历，后序遍历。

算法有递归和非递归2种算法。递归很简单，非递归就比较麻烦，特别是后续遍历的非递归。

算法的理解参照 http://blog.csdn.net/pi9nc/article/details/13008511/ 感谢这位作者的分享，我在看了

算法的基础上以我理解的方式用 java来写

【先序遍历】

//先序遍历递归写法   【根节点-左子树-右子树】
public void preTravel_recrusive(MyBST.Node node){
		if(node==null)
			return;
		System.out.println(node.value);
		if(node.left!=null){
			preTravel_recrusive(node.left);
		}
		if(node.right!=null){
			preTravel_recrusive(node.right);
		}
}
//先序遍历非递归写法  借助了stack这个先进后出的数据结构  
public void preTravel(){
		Stack stack = new Stack();
		if(this.root==null)
			return;
		Node current = this.root;
		//先把root压入栈顶
		stack.push(current);
		while(current!=null || !stack.isEmpty()){
			if(current!=null){
				System.out.println(current.value);
				current = current.left;
			}else{
				current = stack.pop();
				current = current.right;
			}
			if(current!=null)
				stack.push(current);
		}
	}

【中序遍历】

//中序遍历 【左子树-根节点-右子树】

public void midTravel_recrusive(MyBST.Node node){
		if(node==null)
			return;
		if(node.left!=null){
			midTravel_recrusive(node.left);
		}
		System.out.println(node.value);
		if(node.right!=null){
			midTravel_recrusive(node.right);
		}
}
//中序遍历非递归写法  借助了stack这个先进后出的数据结构  
public void midTravel(){
		Stack stack = new Stack();
		Node node = this.root;
		if(node==null)
			return;
		stack.push(node);
		//如果node为空，就要去stack里判断是否为空
		while(node!=null || !stack.isEmpty()){
			if(node!=null){
				node = node.left;
			}else{
				node = stack.pop();
				System.out.println(node.value);
				node = node.right;
			}
			if(node!=null)
				stack.push(node);
		}
}

【后序遍历】

//后序遍历   【左子树-右子树-根节点】 
public void behideTravel_recrusive(MyBST.Node node){
		if(node==null)
			return;
		if(node.left!=null){
			behideTravel_recrusive(node.left);
		}
		if(node.right!=null){
			behideTravel_recrusive(node.right);
		}
		System.out.println(node.value);
}

//非递归后序遍历，这个发了我很长时间调试。
//主要是理解算法和原理，方向对了，剩下的就是不断的测试各种可能性
public void behideTravel(){
		if(this.root==null){
			return ;
		}
		Stack stack = new Stack();
		Node node=null,cur=this.root,pre=null;
		stack.add(cur);
		while(!stack.isEmpty()){
			node=null;
			//注意pre要！=null
			if(cur.right!=null && !(pre!=null && (cur.left==pre||cur.right==pre))){
				stack.add(cur.right);
				node = cur.right;
			}
			//注意pre要！=null
			if(cur.left!=null && !(pre!=null && (cur.left==pre||cur.right==pre))){
				stack.add(cur.left);
				node =cur.left;
			}
			if(node!=null)
				cur = node;
			else{
				pre = cur;
				cur = stack.peek();
				//注意pre要！=null
				if( (cur.right==null || cur.left==null)	|| 
					(pre!=null && (cur.left==pre||cur.right==pre))
				  ){
					System.out.println(cur.value);
					cur = stack.pop();
				}
			}
		}
}

4.删除

public boolean delete(C c){
		Node deleteNode = root;
		//isLeft 删除节点是它的父类的左还是右
		boolean isLeft = false;
		while(deleteNode!=null){
			if(deleteNode.value.compareTo(c)>0){
				deleteNode = deleteNode.left;
				isLeft = true;
			}else if (deleteNode.value.compareTo(c)<0){
				deleteNode = deleteNode.right;
				isLeft = false;
			}else{
				break;
			}
		}
		if(deleteNode==null)
			return false;
		else{
			if(deleteNode.left==null && deleteNode.right==null){//删除的节点是叶子节点
				if(deleteNode.parent==null){//注意头节点
					root = null;
					return true;
				}
				if(isLeft){
					deleteNode.parent.left=null;
				}else{
					deleteNode.parent.right=null;
				}
				deleteNode.parent=null;
			}else if(deleteNode.left!=null && deleteNode.right==null){//删除的节点有left
				if(deleteNode.parent==null){//delete node is root
					root = deleteNode.left;
				}else{
					deleteNode.parent.left=deleteNode.left;
					deleteNode.left.parent=deleteNode.parent;
				}
			}else if(deleteNode.right!=null && deleteNode.left==null){//删除的节点有right
				if(deleteNode.parent==null){//delete node is root
					root = deleteNode.right;
				}else{
					deleteNode.parent.right=deleteNode.right;
					deleteNode.right.parent=deleteNode.parent;
				}
			}else{//have right and left child tree
				Node successor = deleteNode.right;
   // 从删除的节点的右子树里找到最小的值，作为删除节点的父节点的左或右子树
   //（依据于删除节点原来是父节点的左或右）
				while(successor.left!=null){
					successor=successor.left;
				}
				if(isLeft){
					 successor.parent.left = successor.right;
				}else{
					 successor.parent.right = successor.right;
				}
				if(successor.right!=null){
					successor.right.parent=successor.parent;
				}
				
				if(deleteNode.parent==null){//注意删除的节点是头节点
					root = successor;
				}else{
					if(isLeft){
						 deleteNode.parent.left=successor;
					}else{
						 deleteNode.parent.right=successor;
					}
				}
				successor.right=deleteNode.right;
				successor.left=deleteNode.left;
				successor.parent=deleteNode.parent;
			}
			deleteNode.parent=null;
			deleteNode.right=null;
			deleteNode.left=null;
			return true;
		}
	}

在测试的时候要注意各种可能性，多测各种临界条件。

代码在

https://github.com/rechardguo/LearnCase_mvn/tree/master/src/main/java/rechard/learn/datastruct/map