【Stanford|斯坦福-机器学习:线性回归-单特征梯度下降+动态图】python3实现

说明： 本文内容为【吴恩达-Stanford University Machine Learning】的学习总结笔记。

概念：

在吴恩达老师斯坦福机器学习教程第一讲，使用监督方法-线性回归建立模型，线性预估模型函数：

  

设其中X0=1，则有：

使用梯度下降方法计算参数θ：

取得参数θ，即可使用线性回归模型预测数据。

本文内容主要目的是了解梯度下降的实现，及掌握使用matplotlib 库animation可视化梯度下降过程的方法。更多的概念请参考：

1. 网易公开课 斯坦福机器学习教程视频，搜机器学习即可；
2. 网上有很多个人博客有很好的总结：机器学习算法入门之(一) 梯度下降法实现线性回归    、    机器学习入门：线性回归及梯度下降

python实例：单梯度下降+动图过程

按以下步骤实现线性回归-梯度下降：

1. 获取数据(可能会有复杂的ETL过程)；
2. 特征缩放；
3. 梯度下降；
4. 使用matplotlib 库animation动图记录梯度下降过程；

一、获取数据

备注：脚本中涉及数据来自测试数据示例数据。

# 打开训练集文件
    f = open(r"F:\Users\Share\python\data.csv", "r")
    rows = f.readlines()
    # 设训练集为房屋价格
    x1 = []  # 房屋大小 平方米 x∈(25,71) avg=48
    y1 = []  # 房屋价格 万 y∈(30,120) avg=75
    # 转列表存储
    for row in [value.split(",") for value in rows]:
        x1.append(float(row[0]))
        y1.append(float(row[1]))
    # 关闭打开的文件
    f.close()

二、特征缩放

在进行模型训练前，需要对数据进行特征缩放： 将不同特征数据缩放到同一个相似区间内。

# 【1】特征缩放 X:=[X-mean(X)]/std(X) || X:=[X-min(X)]/max(X)-min(X) ;
def feature_scaling(data_set):
    # 特征缩放参数
    max_value = data_set.max(0)
    min_value = data_set.min(0)
    # avg_value = (min_value + max_value)/2
    diff_value = max_value - min_value
    norm_data_set = zeros(shape(data_set))  # 初始化与data_set结构一样的零array
    m = data_set.shape[0]
    norm_data_set = data_set - tile(min_value, (m, 1))  # avg_value
    norm_data_set = norm_data_set/tile(diff_value, (m, 1))
    return norm_data_set, diff_value, min_value

三、单特征梯度下降

（1）线性模型函数：

# def hy(theta, x_sample):
#      # hypothsis = theta0 + theta1 * x1 + theta2 * x2 .....
#     temp = [thetai * xi for thetai, xi in zip(theta, x_sample)]
#     result = sum(temp)
#     return result
def create_hy(θ1, θ0):
    return lambda xi: θ1*xi + θ0

（2）梯度下降：

# 【2】梯度下降  hypothsis = theta0 + theta1 * x1 + theta2 * x2 .....
# α=0.001 0.01 0.03 0.1 0.3 1 3 10
def step_gradient(xa, ya, α=0.001, variance=0.00001):
    # init the parameters to zero
    θ0_temp = θ1_temp = 1.
    θ0_last = θ1_last = 100.
    reduction = 1
    # 循环
    while reduction > variance:
        hypothesis = create_hy(θ1_temp, θ0_temp)
        m = len(xa)
        # 计算θ0、θ1
        θ0_temp -= α * (1./2) * sum([hypothesis(xa[i]) - ya[i] for i in range(m)])
        θ1_temp -= α * (1./2) * sum([(hypothesis(xa[i]) - ya[i]) * xa[i] for i in range(m)])
        # 存储梯度下降过程theta0，theta1
        theta.append((θ0_temp, θ1_temp))
        # 画线
        # for xxi in xx:
        #     yy.append((xxi, theta0_guess+theta1_guess*xxi))
        reduction = min(abs(θ0_temp - θ0_last), abs(θ1_temp - θ1_last))
        θ0_last = θ0_temp
        θ1_last = θ1_temp
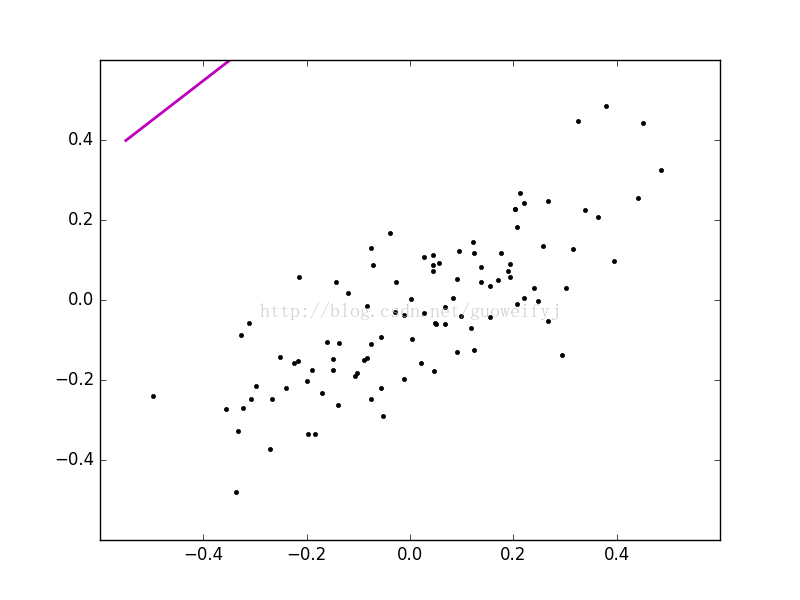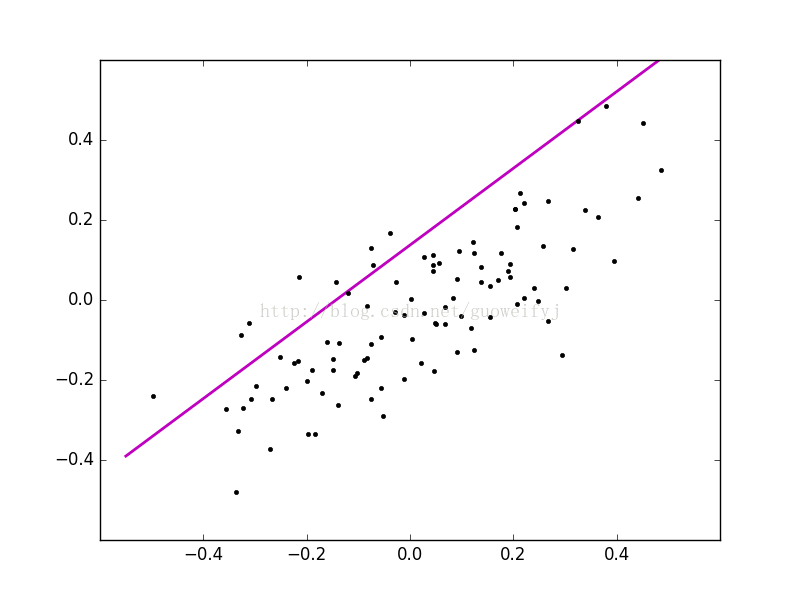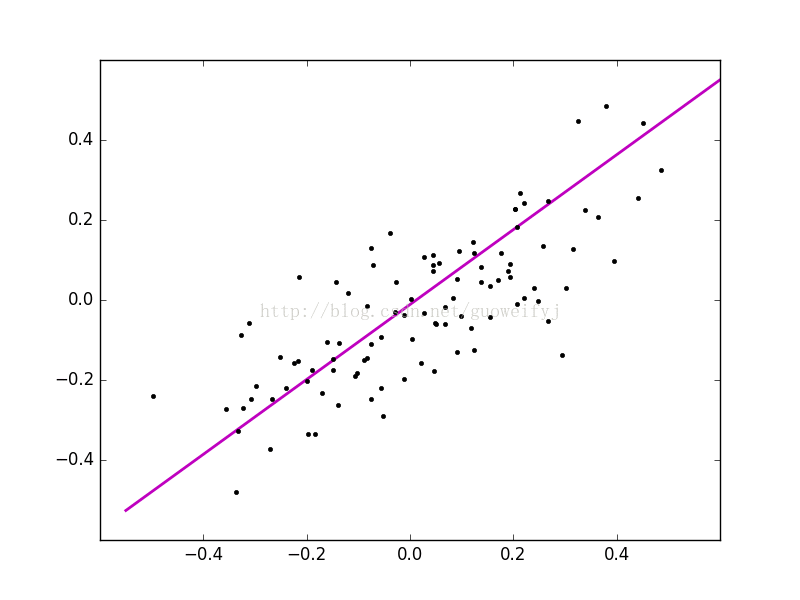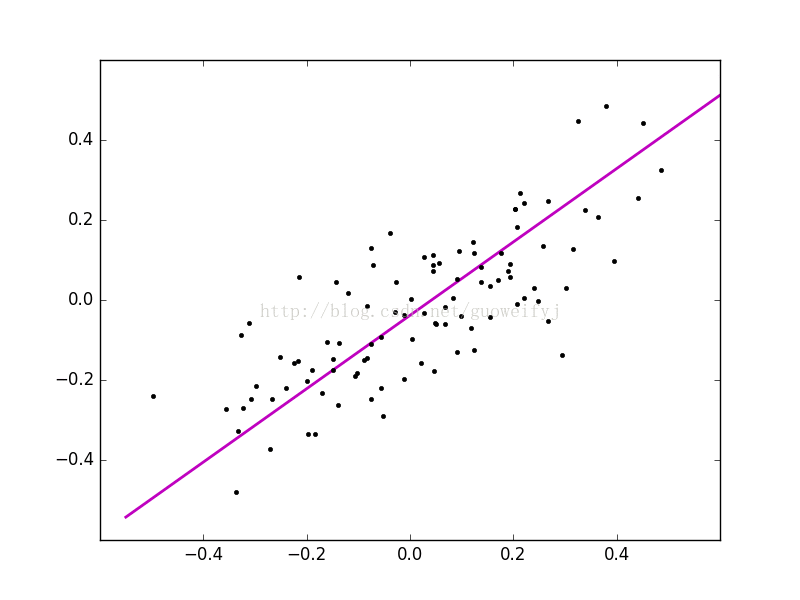
    return θ0_temp, θ1_temp, theta

四、animation动图展示梯度下降过程

使用animation下FuncAnimation函数可以生成动图，记录梯度下降过程，有助于更清晰的掌握算法优化过程，FuncAnimation方法需要两个函数，一个是init()初始化函数，一个是动画循环函数animate，具体如下：

（1）初始化函数：

 # 初始化动画节点
    def init():
        line.set_data([], [])
        plt.plot(x, y, 'bo')
        plt.title('house detail')
        plt.xlabel('size')
        plt.ylabel('price')
        return line

（2）迭代函数：

# 动画循环
    def animate(i):
        global ax, line, label
        yy = []
        θ = thetaArr[i]
        for xxi in xx:
            yy.append(θ[0]+xxi*θ[1])
        line.set_data(xx, yy)
        label.set_position([θ[0], θ[1]])
        return line, label

（3）保存成动图：

# animation动态记录
    anim = animation.FuncAnimation(fig, animate, init_func=init, frames=len(theta), interval=1000, repeat=True)
    # 要保存gif 调小frames参数
    anim.save('D:\MeetYou\Learning\MachineLearning\GradientDescent\GradientDescent.gif'
              , writer='imagemagick', fps=1)

结果展示：

五、完整测试代码实现

# coding=utf-8
# 线性回归-单特征梯度下降练习
from numpy import *
import matplotlib.pyplot as plt
from matplotlib import animation
import numpy as np


# 【1】特征缩放 X:=[X-mean(X)]/std(X) || X:=[X-min(X)]/max(X)-min(X) ;
def feature_scaling(data_set):
    # 特征缩放参数
    max_value = data_set.max(0)
    min_value = data_set.min(0)
    # avg_value = (min_value + max_value)/2
    diff_value = max_value - min_value
    norm_data_set = zeros(shape(data_set))  # 初始化与data_set结构一样的零array
    m = data_set.shape[0]
    norm_data_set = data_set - tile(min_value, (m, 1))  # avg_value
    norm_data_set = norm_data_set/tile(diff_value, (m, 1))
    return norm_data_set, diff_value, min_value


# def hy(theta, x_sample):
#      # hypothsis = theta0 + theta1 * x1 + theta2 * x2 .....
#     temp = [thetai * xi for thetai, xi in zip(theta, x_sample)]
#     result = sum(temp)
#     return result
def create_hy(θ1, θ0):
    return lambda xi: θ1*xi + θ0


# 【2】梯度下降  hypothsis = theta0 + theta1 * x1 + theta2 * x2 .....
# α=0.001 0.01 0.03 0.1 0.3 1 3 10
def step_gradient(xa, ya, α=0.001, variance=0.00001):
    # init the parameters to zero
    θ0_temp = θ1_temp = 1.
    θ0_last = θ1_last = 100.
    reduction = 1
    # 循环
    while reduction > variance:
        hypothesis = create_hy(θ1_temp, θ0_temp)
        m = len(xa)
        # 计算θ0、θ1
        θ0_temp -= α * (1./2) * sum([hypothesis(xa[i]) - ya[i] for i in range(m)])
        θ1_temp -= α * (1./2) * sum([(hypothesis(xa[i]) - ya[i]) * xa[i] for i in range(m)])
        # 存储梯度下降过程theta0，theta1
        theta.append((θ0_temp, θ1_temp))
        # 画线
        reduction = min(abs(θ0_temp - θ0_last), abs(θ1_temp - θ1_last))
        θ0_last = θ0_temp
        θ1_last = θ1_temp
    return θ0_temp, θ1_temp, theta

# 主方法
if __name__ == "__main__":
    # 打开训练集文件
    f = open(r"F:\Users\Share\python\data.csv", "r")
    rows = f.readlines()
    # 设训练集为房屋价格
    x1 = []  # 房屋大小 平方米 x∈(25,71) avg=48
    y1 = []  # 房屋价格 万 y∈(30,120) avg=75
    # 转列表存储
    for row in [value.split(",") for value in rows]:
        x1.append(float(row[0]))
        y1.append(float(row[1]))
    # 关闭打开的文件
    f.close()
    # 特征缩放
    # x, y = feature_scaling1(x1, y1)
    x, diff_x, min_x = feature_scaling(np.array(x1))
    y, diff_y, min_y = feature_scaling(np.array(y1))
    theta = []

    # 线性回归：单特征梯度下降
    t0, t1, thetaArr = step_gradient(x.tolist()[0], y.tolist()[0])
    print("Final result: theta0_guess:%f theta1_guess:%f" % (t0, t1))
    # 绘图
    fig = plt.figure()
    # ax = plt.axes(xlim=(-0.6, 0.6), ylim=(-0.6, 0.6))
    ax = plt.axes(xlim=(-0.5, 1.5), ylim=(-0.5, 1.2))
    line, = ax.plot([], [],  color='m', linewidth=2)
    label = ax.text([], [], '')

    # 初始化动画节点
    def init():
        line.set_data([], [])
        plt.plot(x, y, 'bo')
        plt.title('house detail')
        plt.xlabel('size')
        plt.ylabel('price')
        return line

    xx = [-0.55, 0.0, 0.34, 0.78]  # 画线点

    # 动画循环
    def animate(i):
        global ax, line, label
        yy = []
        θ = thetaArr[i]
        for xxi in xx:
            yy.append(θ[0]+xxi*θ[1])
        line.set_data(xx, yy)
        label.set_position([θ[0], θ[1]])
        return line, label

    # animation动态记录
    anim = animation.FuncAnimation(fig, animate, init_func=init, frames=len(theta), interval=1000, repeat=True)
    # 要保存gif 调小frames参数
    anim.save('D:\MeetYou\Learning\MachineLearning\GradientDescent\GradientDescent.gif'
              , writer='imagemagick', fps=1)
    plt.show()

总结：

从以上python实现示例可以看出：

1. 批梯度下降的收敛速度会比较慢；
2. 必要的特征缩放；
3. 必要的animation动图，让你更了解梯度下降过程。

--------------------------------------------我是分割线--------------------------------------------

高峰屹立，积跬步，行不止。