隐马尔科夫模型一(概念理解)
前言
由于前一段时间在看CTC论文,里面用到了HMM中的前向后向算法,推公式的时候·一脸懵逼,所以又来学习HMM的思想,所以写篇博客做个笔记。本部分博客分为两篇,第一篇主要介绍一些基本的概念和思想,第二篇介绍理论的推导。博客的内容主要是基于<<统计学习方法>>以及其他的一些博客
模型概念
隐马尔可夫模型:隐马尔科夫模型是关于时序的概念模型,描述了由一个隐藏的马尔科夫链随机产生不可观测的状态随机序列,再由各个状态生成一个观测而产生的观测随机序列的过程。隐藏的马尔科夫链随机生成的状态序列成为状态序列:每个状态生成一个观测,而由此产生的观测的随机序列,称为观测序列。序列的每一个位置又可以看作一个时刻。
当第一次看到上述描述时估计大都数人都会和我一样一脸蒙逼,什么是状态序列,什么又是观测序列?还有隐马尔可夫链又是神马?
举个例子,假设你有一个住得很远的朋友,他每天跟你打电话告诉你他那天做了什么.你的朋友仅仅对三种活动感兴趣:公园散步,购物以及清理房间.他选择做什么事情只凭天气.你对于他所住的地方的天气情况并不了解,但是你知道总的趋势.在他告诉你每天所做的事情基础上,你想要猜测他所在地的天气情况。其实这个就是一个隐马尔科夫模型。每一天天气的变化就是一个隐马尔科夫链(即不同状态之间的转换),其有两个状态 “雨"和"晴”,但是你无法直接观察它们,也就是说,它们对于你是隐藏的.每天,你的朋友有一定的概率进行下列活动:“散步”, “购物”, 或 “清理”. 因为你朋友告诉你他的活动,所以这些活动就是你的观察数据。这整个系统就是一个隐马尔可夫模型HMM。
对于上述的例子而言,如果连续持续多天,你的朋友可能根据不同的天气进行不同的活动(当然,这里有一个前提,你的朋友在同一天只能进行一种活动),这几天天气的变化的就是一个隐藏的状态序列,比如说连续五天的天气为[‘晴’,‘雨’,‘雨’,‘晴’,‘雨’](这是在你不看天气预报的前提下o(╯□╰)o),而你的朋友每一天做的活动就组成了观测序列。这样看起来是不是简单多了。如果对这个例子还是不太理解,推荐看看参考资料[2]。
有了上面的例子,下面可以对隐马尔可夫模型进行符号化的定义。
定义
隐马尔科夫模型有初始概率分布、状态转移概率分布以及观测概率分布确定,其形式化定义如下:
设 Q Q Q是所有可能状态集合, V V V是所有可能的观测的集合
Q = { q 1 , q 2 , . . . q N } , V = { v 1 , v 2 . . v M } Q=\{q_1,q_2,...q_N\},\quad V=\{v_1,v_2..v_M\} Q={q1,q2,...qN},V={v1,v2..vM}
其中 N N N是可能的状态数, M M M是可能的观测数。
I I I是长度为 T T T的状态序列, O O O是对应的观测序列。
I = ( i 1 , i 2 . . . i T ) , O = ( o 1 , o 2 , . . . , o T ) I=(i_1,i_2...i_T),\quad O=(o_1,o_2,...,o_T) I=(i1,i2...iT),O=(o1,o2,...,oT)
A是状态转移矩阵:
A = [ a i j ] N × N A=[a_{ij}]_{N\times N} A=[aij]N×N
其中
a i j = P ( i t + 1 = q j ∣ i t = q i ) , i = 1 , 2 , . . . , N ; j = 1 , 2 , . . . , N a_{ij}=P(i_{t+1}=q_j|i_t=q_i),\quad i=1,2,...,N;j=1,2,...,N aij=P(it+1=qj∣it=qi),i=1,2,...,N;j=1,2,...,N
表示的是 t t t时刻处于 q i q_i qi的条件下在 t + 1 t+1 t+1时刻状态转移到 q j q_j qj的概率。
B是观测概率矩阵:
B = [ b j ( k ) ] N × N B=[b_j(k)]_{N\times N} B=[bj(k)]N×N
其中
b j ( k ) = P ( o t = v k ∣ i t = q j ) , k = 1 , 2 , . . . , M ; j = 1 , 2 , . . . , N b_j(k)=P(o_t=v_k|i_t=q_j),\quad k=1,2,...,M; j=1,2,...,N bj(k)=P(ot=vk∣it=qj),k=1,2,...,M;j=1,2,...,N
是在时刻t处于状态 q j q_j qj的条件下生成观测 v k v_k vk的概率
π \pi π 是初始状态概率向量:
π = ( π i ) \pi=(\pi _i) π=(πi)
其中:
π i = P ( i 1 = q i ) , i = 1 , 2 , . . . , N \pi_i=P(i_1=q_i),\quad i=1,2,...,N πi=P(i1=qi),i=1,2,...,N
所以隐马尔科夫模型 λ \lambda λ可以用三元符号表示,即:
λ = ( A , B , π ) \lambda=(A,B,\pi) λ=(A,B,π)
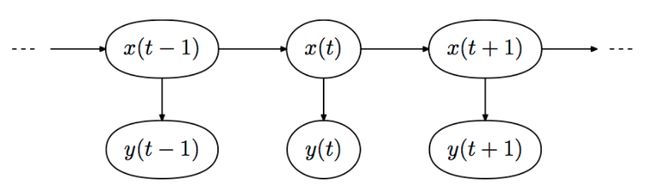
状态转移矩阵 A A A和初始状态概率 π \pi π确定隐藏的马尔科夫链,生成不可观测的状态序列,观测概率矩阵 B B B确定了如何从观测状态生成观测序列。这里从wiki上面盗一张图,上面的 x x x即对应的状态序列, y y y表示的是观测序列:
隐马尔科夫模型的两个性质:
(1)齐次马尔科夫性假设,即使设隐藏的马尔科夫链在任意时刻 t t t的状态只依赖于前一时刻的状态,与其他时刻的状态以及观测无关。
P ( i t ∣ i t − 1 , o t − 1 , . . . , i 1 , o 1 ) = P ( i t ∣ i t − 1 ) P(i_t|i_{t-1},o_{t-1},...,i_1,o_1)=P(i_t|i_{t-1}) P(it∣it−1,ot−1,...,i1,o1)=P(it∣it−1)
这句话是什么意思呢?以上面的图为例,假设 x ( t ) x(t) x(t)表示的状态是前面例子里面的天气,那么 x ( t + 1 ) x(t+1) x(t+1)的天气与 x ( t − 1 ) x(t-1) x(t−1)的天气无关,只与 x ( t ) x(t) x(t)的天气有关。并且也与 y ( t + 1 ) y(t+1) y(t+1)无关。
(2) 观测独立性假设,即假设任意时刻的观测只依赖该时刻的马尔科夫链的状态,与其他观测和状态无关。
P ( o t ∣ i T , o T , i T − 1 , o T − 1 , . . . , i 1 , o 1 ) = P ( o t ∣ i t ) P(o_t|i_T,o_T,i_{T-1},o_{T-1},...,i_1,o_1)=P(o_t|i_t) P(ot∣iT,oT,iT−1,oT−1,...,i1,o1)=P(ot∣it)
意思即为观测状态 o t o_t ot只与对应的 i t i_t it有关。而与其他的状态无关。下面以一个具体例子帮助理解。
盒子与球模型
假设有4个盒子,每一个盒子里面都装有红白两种颜色的球,盒子里面的红白求数有下面表格给出。
| 盒子 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| 红球数 | 5 | 3 | 6 | 8 |
| 白球数 | 5 | 7 | 4 | 2 |
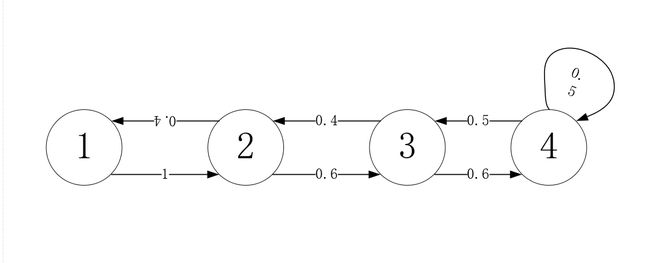
按照下面的方法抽球,并且产生一个关于球的颜色观测序列:首先从四个盒子中等概率随机抽取一个求。记录颜色然后放回盒子,然后根据当前的概率随机转移到下一个盒子。规则是:当前盒子为1,下个盒子一定是2,当前盒子为2或者3。分别以0.4和0.6的概率转移到左边或者右边的盒子,如果当前盒子为4,那么各以0.5的概率转移到盒子3或者停留在盒子4。随机抽取一个球,如此重复5次,得到一个球的颜色的观察序列:
O = { 红 , 红 , 白 , 白 , 红 } O=\{红,红,白,白,红\} O={红,红,白,白,红}
上述过程中,球的颜色序列为观测序列,而抽取的盒子的序列为状态序列。为了清楚表示状态之间的转换,我们将抽盒子规则用马尔可夫链表示出来。
所以盒子对应的状态集合是
Q = { 1 , 2 , 3 , 4 } Q=\{1,2,3,4\} Q={1,2,3,4}
球的颜色的观测集合为:
V = { 红 , 白 } V=\{红,白\} V={红,白}
状态序列和观测序列的长度 T = 5 T=5 T=5
初始分布概率为
π = ( 0.25 , 0.25 , 0.25 , 0.25 ) \pi=(0.25,0.25,0.25,0.25) π=(0.25,0.25,0.25,0.25)
状态转移概率分布为
A = [ 0 1 0 0 0.4 0 0.6 0 0 0.4 0 0.6 0 0 0.5 0.5 ] A= \left[ \begin{matrix} 0 & 1 & 0 & 0 \\ 0.4& 0 & 0.6 & 0\\ 0 & 0.4 & 0 & 0.6\\ 0 & 0 & 0.5 & 0.5 \end{matrix} \right] A=⎣⎢⎢⎡00.400100.4000.600.5000.60.5⎦⎥⎥⎤
观测序列为
B = [ 0.5 0.5 0.3 0.7 0.6 0.4 0.8 0.2 ] B= \left[ \begin{matrix} 0.5 & 0.5\\ 0.3 & 0.7 \\ 0.6 & 0.4 \\ 0.8 & 0.2 \end{matrix} \right] B=⎣⎢⎢⎡0.50.30.60.80.50.70.40.2⎦⎥⎥⎤
三个基本问题
马尔科夫模型的3个基本问题。
(1)概率计算问题。给定模型 λ = ( A , B , π ) \lambda=(A,B,\pi) λ=(A,B,π)和观测序列 O = ( o 1 , o 2 , . . . , o T ) O=(o_1,o_2,...,o_T) O=(o1,o2,...,oT)计算在模型 λ \lambda λ下观测序列为 O O O的概率 P ( O ∣ λ ) P(O|\lambda) P(O∣λ)
(2)学习问题。已知观测序列 O = ( o 1 , o 2 , . . . , o T ) O=(o_1,o_2,...,o_T) O=(o1,o2,...,oT),估计模型 λ = ( A , B , π ) \lambda=(A,B,\pi) λ=(A,B,π)的参数,使得在该模型下观测序列概率 P ( O ∣ λ ) P(O|\lambda) P(O∣λ)最大。
(3)预测问题,也成为解码问题。已知模型 λ = ( A , B , π ) \lambda=(A,B,\pi) λ=(A,B,π)和观测序列 O = ( o 1 , o 2 , . . . , o T ) O=(o_1,o_2,...,o_T) O=(o1,o2,...,oT),求对给定的观测序列概率 P ( I ∣ O ) P(I|O) P(I∣O)的最大值。即给定观测序列,求最有可能的对应状态序列。
三个问题的联系
下面这段是个人理解,可能存在偏差。比如我们以语音识别为例,状态序列对应着我们的输入语音,观测序列对应着输出的标签。学习问题应该是用在训练阶段,给定输入标签以及参数,,训练模型。预测问题则是用模型进行测试,给定了模型和输入,利用模型预测结果。至于第一个问题,应该是被用在训练阶段计算观测序列的概率。关于三个问题的详细推导将在下一张介绍。
参考资料
[1].隐马尔科夫模型,维基百科
[2].漫谈 HMM:Definition, pluskid的博客
[3].统计学习方法,李航
[4].数学之美,吴军