关于Python杂七杂八的小东西(搭建Pycharm+Anaconda、删除文档首行小程序、皮尔逊相关系数小程序)
好久没有回来更新博客了,良心难安啊!最近要做脑电信号的分析,由于导出的数据都是文本格式的,就下定决心放弃Matlab,用Python做分析,确实是挺好用的。下面就把我期间用到的杂七杂八的东西列出来,作为备忘和给需要的朋友的参考吧。
一、搭建Pycharm+Anaconda
我之前用的是Anaconda自带的Spyder编译器,界面还是很友好的,与Matlab高度相似。我觉得最实用的功能就是可以看得到变量的内容,这一点比较类似于Matlab。举个例子,如果我们定义一个矩阵Data,Spyder就可以很方便的看到Data里面的具体内容。但是Spyder用于工程开发的话就不是很适合了,所以我决定改用Pycharm+Anaconda。我的看法是如果用Python做科研的话还是用Spyder比较好,做工程的话最好用Pycharm+Anaconda,两者之间并不存在哪一个绝对比另一个好的问题。
Anaconda里面集成了很多关于python科学计算的第三方库,避免了自行安装库的麻烦,一步到位,特别好用。Pycharm是一个很好的用于开发的IDE,界面友好,使用方便,主要的缺点是在科学计算方面略有欠缺,这个缺点正好由Anaconda补上。
1、下载Anaconda
在官网按自己的需求下载,官网链接https://www.continuum.io/downloads 。下载之后按部就班安装就好。

2、下载Pycharm
同样是到官网按自己的需求下载,官网链接http://www.jetbrains.com/pycharm/download/#section=windows。下载之后按部就班安装就好。这里建议如果不是特别专业的朋友选社区版(Community)就好了,毕竟社区版是免费的并且功能也足够用了。
3、配置环境
都下载安装完毕之后,打开Pycharm,选择File菜单下的Settings选项,找到Project–Project Interpreter。将图中红圈里面的路径更改为之前安装Anaconda路径下的python.exe的路径。如果这里找不到我们安装Anaconda的路径,点击旁边的小齿轮,选择“Add Local”,就可以自行添加了。这时候会发现下面出现了一大堆库,这些库都是Anaconda带给我们的,极大地节约了下载安装库的时间。至此Pycharm+Anaconda搭建完毕。 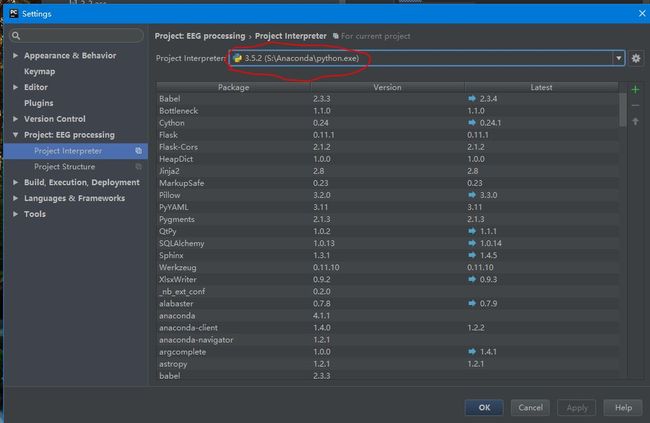
二、删除文档首行小程序
代码如下所示,中心思想是新建一个文档,将原文档中第一行以下的数据写入新文档中。用到的核心函数是'a'.join(b),其作用是以a作为分隔符,将b所有的元素合并成一个新的字符串。
'''删除EEG文件的前两行'''
def delstring(filename):
fin = open(filename)
raw = fin.readlines()
fout = open('new'+filename,'w')
new =''.join(raw[1:]) # 'a'.join(b) 以a作为分隔符,将b所有的元素合并成一个新的字符串
fout.write(new)
fin.close()
fout.close()
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
三、皮尔逊相关系数小程序
这个小程序是参考http://www.cnblogs.com/ryuham/p/4764015.html写出来的,可以用来求两段信号的皮尔逊相关系数。说到皮尔逊相关系数,根据http://changfengmingzhi.blog.163.com/blog/static/1671052882014101810481936/里面的描述,摘抄出如下定义:
在统计学中,皮尔逊积矩相关系数(Pearson product-moment correlation coefficient)用于度量两个变量X和Y之间的相关(线性相关),其值介于-1与1之间。系数的值为1意味着X 和 Y可以很好的由直线方程来描述,所有的数据点都很好的落在一条 直线上,且 Y 随着 X 的增加而增加。系数的值为-1意味着所有的数据点都落在直线上,且 Y 随着 X 的增加而减少。系数的值为0意味着两个变量之间没有线性关系。当两个变量独立时,相关系数为0,但反之并不成立。 这是因为相关系数仅仅反映了两个变量之间是否线性相关。比如说,X是区间[-1,1]上的一个均匀分布的随机变量,而 Y=X2. 那么Y是完全由X确定。因此Y 和X是不独立的,但是相关系数为0。
皮尔逊相关系数的计算公式为:
代码实现如下:
'''两段信号的皮尔逊相关性分析'''
'''求乘积之和'''
def multipl(a,b):
sumofab = 0.0
for i in range(len(a)):
temp = a[i] * b[i]
sumofab += temp
return sumofab
'''求皮尔逊相关系数'''
def corrcoef(x, y):
n = len(x)
sum1 = sum(x)
sum2 = sum(y) # 求和
sumofxy = multipl(x,y) # 求乘积之和
sumofx2 = sum([pow(i, 2) for i in x])
sumofy2 = sum([pow(j, 2) for j in y]) # 求平方和
num = sumofxy - (float(sum1) * float(sum2) / n)
den = sqrt((sumofx2 - float(pow(sum1, 2)) / n) * (sumofy2 - float(pow(sum2, 2)) / n)) # 计算皮尔逊相关系数
return list(map(float,num / den))
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22