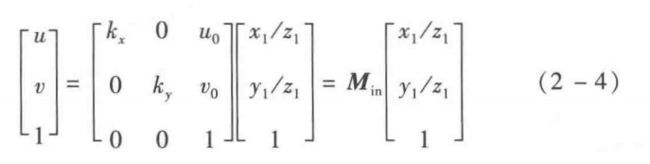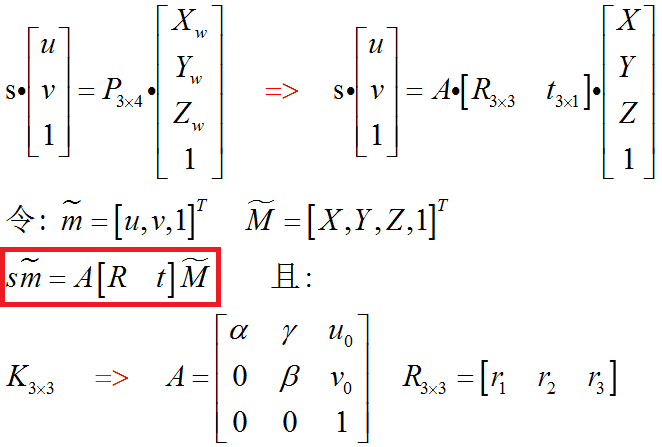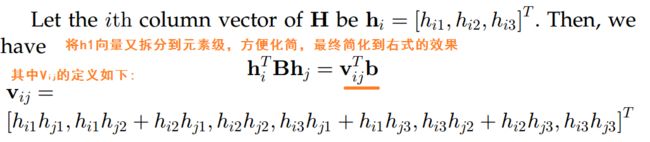相机模型及相机标定原理详解

相机模型

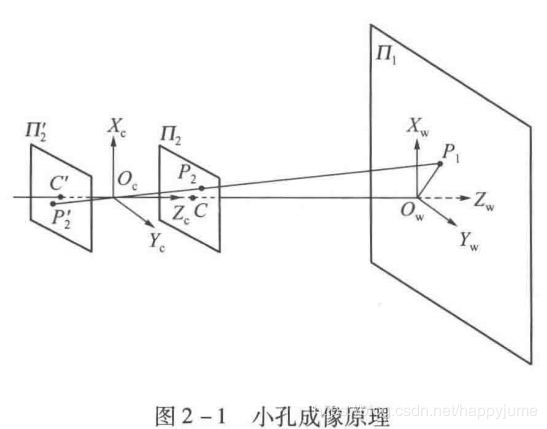
除进行高精度尺寸测量使用远心镜头外，我们正常使用的相机镜头都是普通镜头，其成像模型都是理想的小孔成像模型。

我们在光轴中心处建立坐标系，Z轴方向平行于光轴，正方向为相机到拍摄对象的方向，X方向取图像坐标系的方向，可以理解为上述平面的X轴。根据上图，我们可以得到相机模型中重要的几个坐标系：世界坐标系、相机坐标系（Xc、Oc、Yc组成）、像平面坐标系，还有像素坐标系。其中像平面坐标系和像素坐标系（u，O0，v）之间的关系如下图：

像平面坐标系的原点在像素坐标系的中间，不考虑像平面坐标系和像素坐标系间的缩放，理想情况下（u0，v0）为分辨率的1/2。

在相机坐标系下，设空间中一点P1的坐标为（x1，y1，z1），其在像平面的成像点P2坐标为（x2，y2，z2），则有：

其中f为相机的焦距，f = z2。

相机内参模型

相机的内参可以理解描述相机坐标系和像素坐标系间的模型。

成像平面上的像经过放大处理得到数字图像，像平面上的成像点（x2，y2）经过转换成像素坐标系中的（u，v）点，则有:

由此可以得到：

用矩阵的形式表示：

其中：是x轴方向的放大系数；是Y轴方向的放大系数；成为相机的内参矩阵，因其含有4个参数，也称为相机的四参数模型，也是实际中应用最多的一种模型；（x1，y1，z1）是点在相机坐标系下的坐标。

一般地，点在相机坐标系下用（xc，yc，zc）表示，因此，上式一般改写为：

如果考虑放大系数kx与ky的差异和x轴与y轴间的耦合，则构成的相机内参模型具有5个参数，如下：‘

相机外参模型

相机的外参模型是世界坐标系在相机坐标系中的表示，也可以理解从相机坐标系到世界坐标系的变换。

熟悉三维坐标变换的朋友可以看出，上述外参矩阵可以分为左上角的旋转矩阵R和右上列队T，也即相机坐标系到世界坐标系的RT。

畸变模型

实际成像时，由于镜头的制造工艺和装配误差等原因，成像时会出现畸变。其中由透镜的形状引起的畸变称为径向畸变，由相机组装过程中透镜和成像面不严格平行引起的畸变称为切向畸变。

相机标定

根据上述介绍，四个与相机模型有关的坐标系之间的关系可以用下图来表示：

也可以这么说，相机标定的目的就是确定内参、外参和各个畸变系数。

关于相机标定，此处搬运别人的博客（https://blog.csdn.net/humanking7/article/details/44756235）

上述推导的公式可总结如下：

符号规定( Notation )

为了和 张正友教授 的论文相统一，现在把公式符号统一一下。

推导中的数学基础

第一点 : 旋转向量 R 为正交矩阵，所以又以下的性质：

第二点 : 就是 S 。它是尺度因子，它的出现只是为了方便运算，而且对于齐次坐标，尺度因子不会改变坐标值 。

 

Step.1 标定平面到图像平面的单应性(Homography)

刚开始不知道论文中 Homography 不知道是何方神圣，搜索到了最后这番解释：

因为张氏标定是一种基于平面棋盘格的标定，所以想要搞懂张氏标定，首先应该从两个平面的单应性(Homography)映射开始着手。

单应性(Homography) ： 在计算机视觉中被定义为一个平面到另一个平面的投影映射。首先看一下，图像平面与标定物棋盘格平面的单应性。

因为标定物是平面，所以我们可以把世界坐标系构造在 Z = 0 的平面上。然后进行单应性计算。令 Z = 0 可以将上式转换为如下形式 ( 直接截取论文中的推导 ) ：

分析：

H 是一个3x3的矩阵，并且有一个元素作为齐次坐标。因此，H有8个未知量待解 ( 可以分析一下， A 有5个未知量，后面的 [r1,r2,t] 有三个未知量，一共8个) 。

(X,Y) 作为标定物的坐标，可以由设计者人为控制，是已知量 。 (u,v) 是像素坐标，我们可以直接通过摄像机获得。一组对应的 (X,Y) => (u,v) 我们可以获得两组方程。

现在有 8个未知量 待求，所以至少要8个方程。所以至少需要4组对应的点。所以有 4组 (X,Y) => (u,v)就可以算出，图像平面到世界平面的 单应性矩阵H ，这也是张正友标定采用四个角点的棋盘作为标定物的一个原因 (？不知道是否正确) 。

Step.2 利用约束条件求解内参矩阵A

从Step1可知，应用4个点我们可以获得单应性矩阵H。但是H是内参阵和外参阵的合体。我们想要最终分别获得内参和外参。所以需要想个办法，先把内参求出来。然后外参也就随之解出了。

上式中的 h1,h2 是通过求解单应性矩阵 H 求出来的，所以未知量只剩下 内参矩阵A 。 A中含有5个参数，如果需要完全解出来这5个未知量，则需要 3个不同的单应性矩阵H ( 因为 3个不同的单应性矩阵H在2个约束条件下可以产生6个方程 ) ， 那么如何得到 3个不同的单应性矩阵H 呢？ 那就是 3张不同的标定平面的照片， 我们大多是通过改变摄像机与标定板间的相对位置来获得不同的标定照片。( 如果用2张照片进行标定，就要舍去一个内参 r=0)

当然这只是张正友标定法不断变换标定板方位的 第一个原因 。第二个原因 是张正友提到的 最大似然估计 ( Maximum-Likelihood Estimation ) ( 这个我还得学习 ) 。

现在开始数学课了：

首先令

可以看出 矩阵B 是一个对称矩阵，有效的元素只有 6个 ，所以令一个 6维的向量b ，然后简化公式 ( 就是那两个约束条件 )

将运算的结果带入到两个约束条件中，可得到方程组：

英文部分也提出了3张图片的作用 ( 不懂的可以再看看前面的分析 )

应用上述公式解出b后，就得到了B，在进行 cholesky分解 就可以得到 摄像机内参矩阵A 。

Step.3 利用内参矩阵A求解外参矩阵

已经有了内参矩阵A，通过下面的公式，就可以解出来，外参矩阵了。

 

参考资料：

《机器人视觉测量与控制》

https://blog.csdn.net/humanking7/article/details/44756235

https://blog.csdn.net/tiantangzixue/article/details/79878996

http://www.cnblogs.com/wangguchangqing/p/8335131.html