计算MTF(SFR)的基本步骤,及sfrmat3和Mitre SFR 1.4进行比较
下载sfrmat3 的网址为: http://www.i3a.org/resources/
获得Mitre SFR 1.4参考的网址为:http://www.mitre.org/tech/mtf/
Mitre SFR 1.4和sfrmat3是基于ISO 12233标准,但在某些方面彼此不同:Mitre SFR 1.4旨在尽可能接近标准,而sfrmat3包含一些改进,可以获得精确的结果 即使被测试的图像质量极低。
两者的不同可以从以下几个方面计算:
1、强度(RGB到Y的转换)
Y = Kr*R + Kg*G + Kb*B
为了计算图像的亮度,可以选择以下两种转换:
BT.709: Kr = 0.2126; Kg = 0.7152; Kb = 0.0722;
BT.601: Kr = 0.299; Kg = 0.587; Kb = 0.114;
SFR 1.4只能处理黑白图像,而sfrmat3选择的转换标准是BT.709
2、边缘检测
这是计算SFR的第一步,也是最重要的一步。 最小化边缘检测的误差对是否获得准确的结果至关重要。通常通过分析每个像素线的线性扩展函数来检测边缘。 ISO 12233提到使用有限差分方案[-1,0,1]和[-1,1]。 sfrmat,Mitre SFR 1.4和Quick MTF使用方案[-1,1]。 在计算线的质心之前,sfrmat应用汉明窗,但是Mitre SFR 1.4只是计算质心,没有应用汉明窗。 在计算质心之前应用汉明窗使边缘检测更加稳定。 否则,边缘检测的错误可能会损坏测试结果,不仅在测试质量不是很好的图像时,而且甚至在其他情况下也很常见(图1)。
快速MTF提供三种边缘检测选项:
l 质心
l 质心+汉明窗
l 基于图像的强度
如果使用“基于亮度”选项,则快速MTF不会计算质心和LSF,但只能通过分析亮度分布来检测边缘。
一方面,在计算SFR时,即使倾斜角度的微小误差也可能导致很大的错误[1]。另一方面,小的移动实际上并不影响计算结果。 快速MTF可以精度的检测到边缘的位置。
严重的几何失真或与噪声电平可能使边缘检测变得困难; 在这种情况下,可以选择性关闭Quick MTF中的线性回归。
图.1 计算距心时斜率产生误差的一个例子。 在这种情况下,计算结果是没有意义的。
3、超采样计算边缘扩展函数(ESF)
在该步骤中,考虑到边缘的位移,在同一条亮度线上的亮度被累积和求平均。 sfrmat3和Mitre SFR 1.4以采用4倍超采样的方式进行此操作。
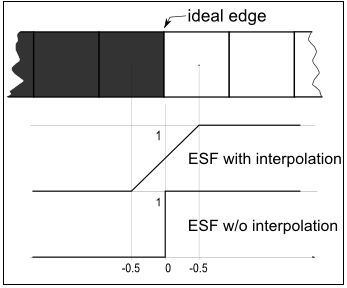
图.2 黑色像素与白色像素之间的理想边缘有无插值时的不同ESF
用超采样(插值)获得的结果看起来更有意义,两种方法都采用了4倍超采样的方法,不过值的取舍中有一点小不同,sfrmat3取值是相同截距的点所在的直线,SFR 1.4是从0到4倍图像宽度的点所在的直线。
4、线扩展函数
LSF是ESF关于坐标的一阶导数。 为了计算导数,Quick MTF可以选择两种差异方案之一:[-1,0,1]和[-1,1]。 sfrmat3使用方案[-1,0,1],而Miter SFR 1.4使用[-1,1]。
在快速MTF,sfrmat或Mitre SFR 1.4中计算LSF后,将汉明窗口应用于LSF。(此步骤与检测边缘之前计算质心时应用汉明窗口无关)。
5、计算SFR
SFR是LSF的傅里叶变换的绝对值。 当转换完成时,在计算LSF的步骤中使用的有限差分校正[2]被应用于结果。 sfrmat3和Mitre SFR 1.4都应用相同的校正。
在比较差异方案[-1,0,1]和[-1,1]的结果。计算结果差异很小但明显。 当修正时,两个差异方案的结果几乎是不可区分的。 所以,你可以看到,修正真的提高了计算的准确性。
Oleg Kurtsev ([email protected]) © 2011
1. Greer PB, van Doorn T. "Evaluation of an algorithm for the assessment of the MTF using an edge method." Med Phys. 2000 Sep; 27(9):2048-59.
2. I. A. Cunningham and A. Fenster "A method for modulation transfer function determination from edge profiles with correction for finite-element differentiation." Med. Phys. 14, 533 (1987).