【数据结构】数据结构中常用的树
声明:本文汇总了数据结构中一些常用的树,主要内容来自《数据结构(严蔚敏版)》和《算法导论》这两本教材。本文主要归纳出数据结构中常见的树的概念与简单的性质,并未给出具体的操作,如插入、删除、查找等。
1、树的定义
首先给出树的相关定义:树(tree)是包含n(n>0)个结点的有穷集,其中:
1)每个元素称为结点(node);
2)有一个特定的结点被称为根结点或树根(root);
3)除根结点之外的其余数据元素被分为m(m≥0)个互不相交的集合T1,T2,……Tm-1,其中每一个集合Ti(1<=i<=m)本身也是一棵树,被称作原树的子树。
树也可以这样定义:树是由根结点和若干颗子树构成的。树是由一个集合以及在该集合上定义的一种关系构成的。集合中的元素称为树的结点,所定义的关系称为父子关系。父子关系在树的结点之间建立了一个层次结构。在这种层次结构中有一个结点具有特殊的地位,这个结点称为该树的根结点,或称为树根。
2、树的相关术语
节点的度:一个节点含有的子树的个数称为该节点的度;
叶节点或终端节点:度为0的节点称为叶节点;
非终端节点或分支节点:度不为0的节点;
双亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点;
孩子节点或子节点:一个节点含有的子树的根节点称为该节点的子节点;
兄弟节点:具有相同父节点的节点互称为兄弟节点;
树的度:一棵树中,最大的节点的度称为树的度;
节点的层次:从根开始定义起,根为第1层,根的子节点为第2层,以此类推;
树的高度或深度:树中节点的最大层次;
堂兄弟节点:双亲在同一层的节点互为堂兄弟;
节点的祖先:从根到该节点所经分支上的所有节点;
子孙:以某节点为根的子树中任一节点都称为该节点的子孙。
森林:由m(m>=0)棵互不相交的树的集合称为森林;
下面给出常见的树的概念,大部分内容可参考严蔚敏版《数据结构》:
3、二叉树
二叉树是数据结构中一种重要的数据结构,也是树表家族最为基础的结构。
二叉树的定义:二叉树的每个结点至多只有二棵子树(不存在度大于2的结点),二叉树的子树有左右之分,次序不能颠倒。二叉树的第i层至多有2i-1个结点;深度为k的二叉树至多有2k-1个结点;对任何一棵二叉树T,如果其终端结点数为n0,度为2的结点数为n2,则n0=n2+1。
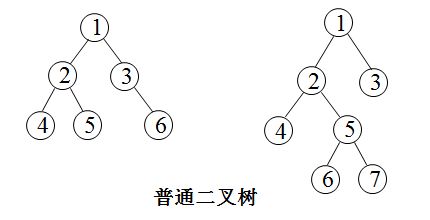
4、满二叉树
一棵深度为k且有2k-1(2的k次幂减1)个结点的二叉树称为满二叉树。
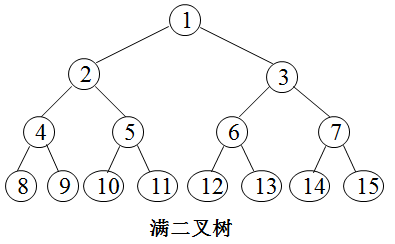
5、完全二叉树
深度为k的,有n个结点的二叉树,当且仅当其每一个结点都与深度为k的满二叉树中编号从1至n的结点一一对应时,称之为完全二叉树。
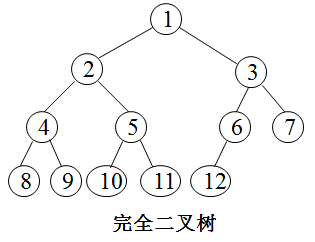
6、二叉排序树
二叉查找树定义:又称为是二叉排序树(Binary Sort Tree)或二叉搜索树。二叉排序树或者是一棵空树,或者是具有下列性质的二叉树:
1) 若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值;
2) 若它的右子树不空,则右子树上所有结点的值均大于或等于它的根结点的值;
3) 它的左、右子树也分别为二叉排序树。

7、平衡二叉树
平衡二叉树(Balanced Binary Tree)又被称为AVL树。它或者是一棵空树,或者是具有下列性质的二叉树:它的左子树和右子树都是平衡二叉树,且左子树和右子树的深度之差的绝对值不超过1。(注:平衡二叉树应该是一棵二叉排序树)

下面给出高级一点的树的数据结构,这些树在面试的时候会被经常提及:
8、B树
B树又称为B-树,是一种平衡的多路查找树。B-树的阶是所有结点的孩子结点树的最大值。一棵m阶B-树,或为空树,或为满足下列特性的m叉树:
1)树中每个结点至多有m棵子树;
2)若根节点不是叶子节点,则至少有两棵子树;
3)除根之外的所有非终端结点至少有[m/2]()向上取整)棵子树;
4)所有的非终端结点中包含下列信息数据:(n,A0,K1,A1,K2,A2,…,Kn,An),其中,n为结点中的关键字树,A为指向子树根结点的指针,K为关键字,且Ai-1所指子树中所有结点的关键字均小于Ki,An所指子树中所有结点的关键字均大于Kn;
5)所有的叶子结点都出现在同一层次上,并且不带信息(可以看作是外部结点或查找失败的结点,实际上这些结点不存在,指向这些结点的指针为空)。下图为一棵4阶B-树:

9、B+树
B+树是应文件系统所需而出的一种B-树的变型树。一棵m阶B+树和m阶的B-树的差异在于:
1)有n棵子树的结点中含有n个关键字,每个关键字不保存数据,只用来索引,所有数据都保存在叶子节点;
2)所有的叶子结点中包含了全部关键字的信息,及指向含这些关键字记录的指针,且叶子结点本身依关键字的大小自小而大顺序链接;

10、红黑树
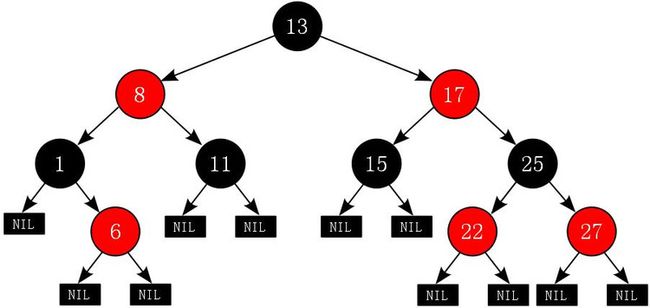
红黑树,一种二叉查找树,但在每个结点上增加一个存储位表示结点的颜色,可以是Red或Black。通过对任何一条从根到叶子的简单路径上各个结点的颜色进行约束,红黑树确保没有一条路径会比其他路径长出2倍,因而是近似于平衡的。树中每个结点包含5个属性:color、key、left、right和p。如果一个结点没有子节点或父节点,则该结点相应的指针属性值为NIL,我们可以把这些NIL视为指向二叉搜索树的叶节点(外部结点)的指针,而把带关键字的结点视为树的内部结点。
一棵红黑树是满足下面性质的二叉搜索树:
1)每个结点或是红色的,或是黑色的;
2)根结点是黑色的;
3)每个叶结点(叶结点即指树尾端NIL指针或NULL结点)是黑的;
4)如果一个结点是红色的,则它的两个子结点都是黑色的;
5)对每个结点,从该结点到其所有后代叶结点的简单路径上,均包含相同数目的黑色结点。
红黑树虽然本质上是一棵二叉查找树,但它在二叉查找树的基础上增加了着色和相关的性质使得红黑树相对平衡,从而保证了红黑树的查找、插入、删除的时间复杂度最坏为O(log n)。
11、键树
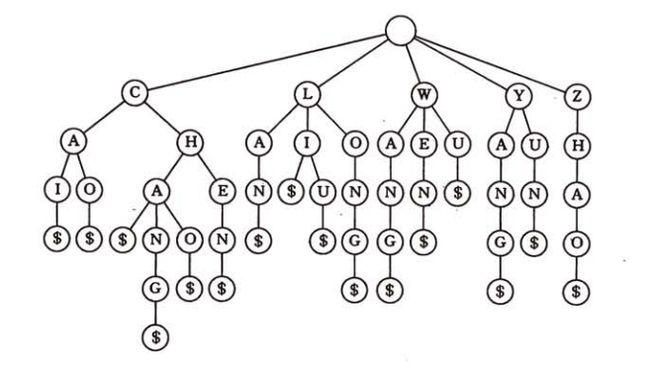
如果一个关键字可以表示成字符的序号,即字符串,那么可以用键树(keyword tree),又称数字搜索树或字符树,来表示这样的字符串的集合。键树的结构受启发于一部大型字典的“书边标目”。字典中标出首字母是 A,B,C,…,Z的单词所在页,再对各部分标出第二字母为A,B,C,…,Z的单词所在的页等等。
键树是一种特殊的查找树,它是一棵度大于等于2的树,树中的每个节点不是包含一个或几个关键字,而是只含有组成关键字的符号。
比如:如果关键字是数值,则节点中只包含一个数位;如果关键字是单词,则节点中只包含一个字母字符。根结点不代表任何字符,根以下第一层的结点对应于字符串的第一个字符,第二层的结点对应于字符串的第二个字符……每个字符串可由一个特殊的字符如“$”等作为字符串的结束符,用一个叶子结点来表示该特殊字符。把从根到叶子的路径上,所有结点(除根以外)对应的字符连接起来,就得到一个字符串。因此,每个叶子结点对应一个关键字。在叶子结点还可以包含一个指针,指向该关键字所对应的元素。整个字符串集合中的字符串的数目等于叶子结点的数目。如果一个集合中的关键字都具有这样的字符串特性,那么,该关键字集合就可采用这样一棵键树来表示。
键树的存储通常有两种方式:
1)用树的孩子兄弟链来表示键树,称为双链树;每个Node有三个域:symbol域:存储关键字的一个字符;son域:存储指向第一棵子树的根的指针;brother域:存储指向右兄弟的指针。
2)用多重链表来表示键树,称为Trie树或字典树。
12、字典树
如果以树的多重链表来表示键树,则树的每个结点应包含d个(d为关键字符的基,如:字符集由英文大写字母构成时,则d=26)指针域,此时的键树又称为字典树。
字典树典型应用是用于统计,排序和保存大量的字符串(但不仅限于字符串),所以经常被搜索引擎系统用于文本词频统计。它的优点是:利用字符串的公共前缀来减少查询时间,最大限度地减少无谓的字符串比较,查询效率比哈希树高。
Tire树的三个基本性质:
1) 根节点不包含字符,除根节点外每一个节点都只包含一个字符;
2) 从根节点到某一节点,路径上经过的字符连接起来,为该节点对应的字符串;
3) 每个节点的所有子节点包含的字符都不相同。
Tire树的应用:
1) 串的快速检索
给出N个单词组成的熟词表,以及一篇全用小写英文书写的文章,请你按最早出现的顺序写出所有不在熟词表中的生词。在这道题中,我们可以用数组枚举,用哈希,用字典树,先把熟词建一棵树,然后读入文章进行比较,这种方法效率是比较高的。
2) “串”排序
给定N个互不相同的仅由一个单词构成的英文名,让你将他们按字典序从小到大输出。用字典树进行排序,采用数组的方式创建字典树,这棵树的每个结点的所有儿子很显然地按照其字母大小排序。对这棵树进行先序遍历即可。
3) 最长公共前缀
13、后缀树
所谓后缀树,就是包含一则字符串所有后缀的压缩了的字典树。先说说后缀的定义。给定一长度为n的字符串S=S1S2..Si..Sn,和整数i,1 <= i <= n,子串SiSi+1…Sn都是字符串S的后缀。以字符串S=XMADAMYX为例,它的长度为8,所以S[1..8],S[2..8], … , S[8..8]都算S的后缀,我们一般还把空字串也算成后缀。这样,我们一共有如下后缀。对于后缀S[i..n],我们说这项后缀起始于i。
键树只适合前缀匹配和全字匹配,并不适合后缀和子串匹配,而后缀树在这方面则非常合适。它与键树的最大不同在于,后缀树的单词集合是由指定字符串的后缀子串构成。
14、区间树与线段树
区间树是在红黑树基础上进行扩展得到的支持以区间为元素的动态集合的操作,其中每个节点的关键值是区间的左端点。通过建立这种特定的结构,可是使区间的元素的查找和插入都可以在O(lgn)的时间内完成。相比于基础的红黑树数据结构,增加了一个max[x],即以x为根的子树中所有区间的端点的最大值。
线段树是一种平衡二叉查找树,它将一个区间划分成一些单元区间,每个单元区间对应线段树中的一个叶结点。主要的处理思想是基于分治的思想。
设根节点的区间为[a,b),区间长度为L = b - a,线段树的性质:
1)线段树是一个平衡树,树的高度为log(L);
2)线段树把区间上的任意长度为L的线段都分成不超过2log(L)线段。
15、败者树与胜者树
胜者树和败者树都是完全二叉树,是树形选择排序的一种变型。在胜者树、败者树中,每个叶子结点相当于一个选手,每个中间结点相当于一场比赛,每一层相当于一轮比赛。不同的是,胜者树中的每个非终端结点均表示其左、右孩子结点中的“胜者”;而在败者树中,父结点中记下刚进行完的这场比赛中的败者,而让胜者去参加更高一层的比赛。下图为一棵实现5路归并排序的败者树: