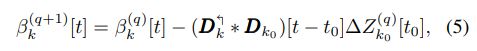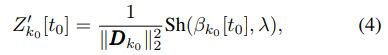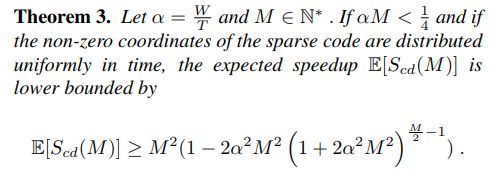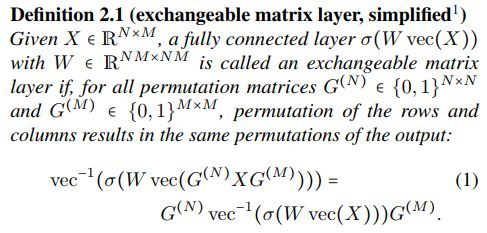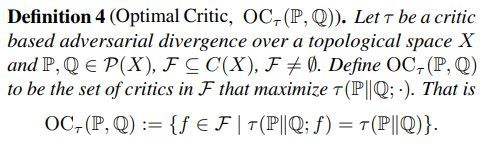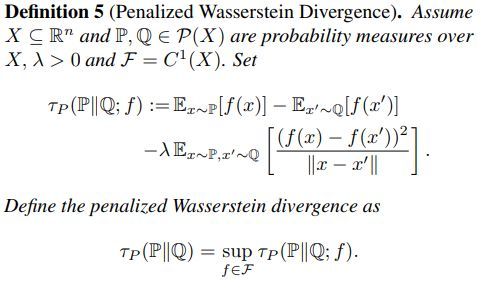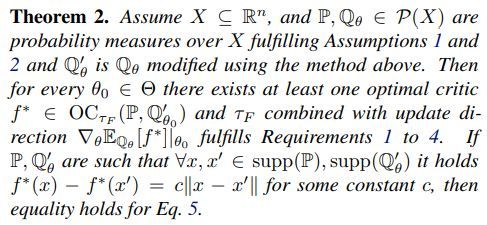ICML 2018 深度学习论文及代码集锦(7)
[1] DICOD: Distributed Convolutional Coordinate Descent for Convolutional Sparse Coding
Moreau Thomas, Oudre Laurent, Vayatis Nicolas
CNRS, Universite Paris-Saclay, Universite Paris
http://proceedings.mlr.press/v80/moreau18a/moreau18a.pdf
本文提出一种新的算法,Distributed Convolution Coordinate Descent (DICOD),用于卷积稀疏编码。该算法是分布式的,并且基于坐标梯度法。
贪婪式坐标下降算法伪代码如下
其中(5)式为
(5)式中的sh函数定义如下
本文所提出的DICOD算法伪代码如下
其中(4)式为
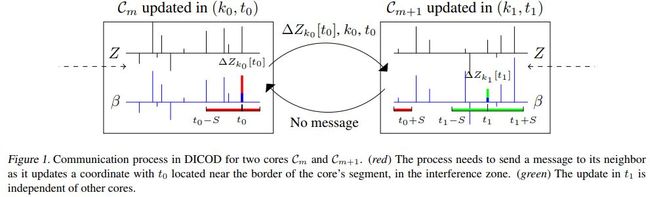
DICOD是一种分布式算法,必然存在通讯,该算法中的通讯过程示例如下
局部贪婪式坐标下降算法伪代码如下
命题一
定理二
其中(2)定义如下
定理三
推论四
各算法随迭代次数和运行时间变化的趋势对比如下
其中CD为coordinate descent;
RCD为randomized coordinate descent;
FCSC为Fast Convolutional Sparse Coding;
FISTA为Fast Iterative Soft Thresholding Algorithm
代码地址
github.com/tomMoral/dicod
[2] Deep Models of Interactions Across Sets
Jason Hartford, Devon R Graham, Kevin Leyton-Brown, Siamak Ravanbakhsh
University of British Columbia
http://proceedings.mlr.press/v80/hartford18a/hartford18a.pdf
本文所提设计的三个优势在于
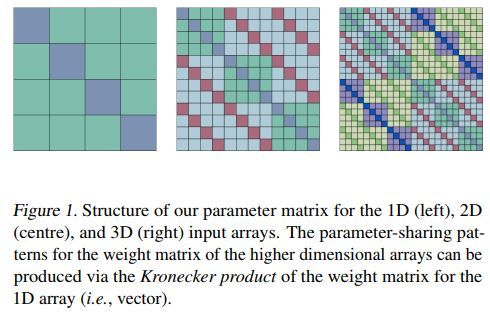
一维 二维 三维的参数矩阵示例如下
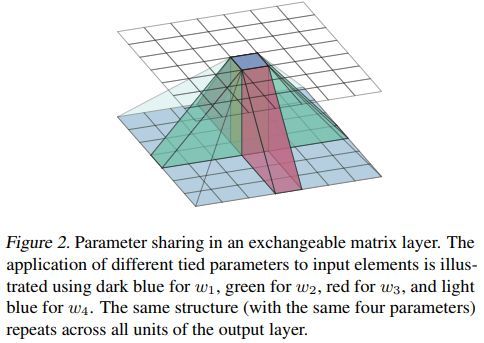
可交换矩阵层参数共享机制示例如下
可交换矩阵层的定义如下
定理2.1 如下
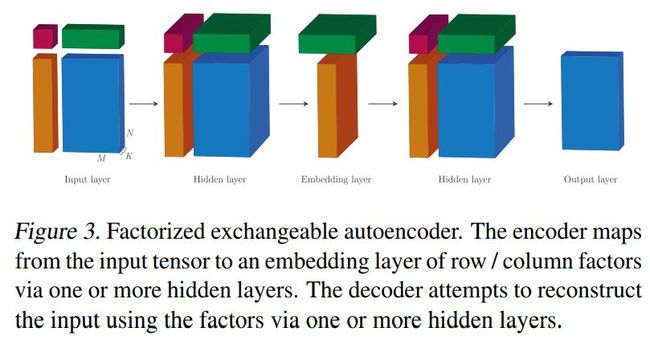
分解机可交换自编码结构示例如下
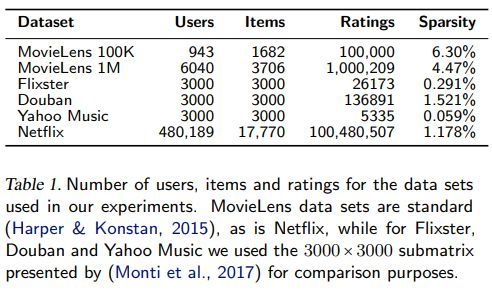
数据集信息如下
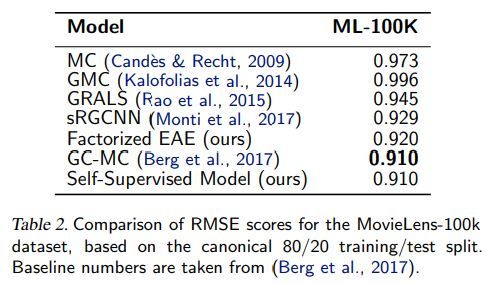
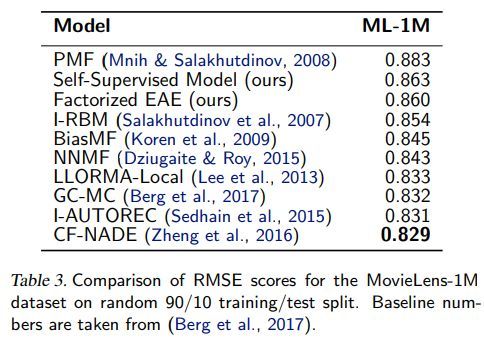
各方法效果对比如下
其中是sRGCNN为separable recurrent multi-graph CNN
GC-MC 为graph convolutional matrix completion
其中I-autorec为item-based autoencoder framework for collaborative filtering
CF-NADE 为Neural Autoregressive Distribution Estimator based CF
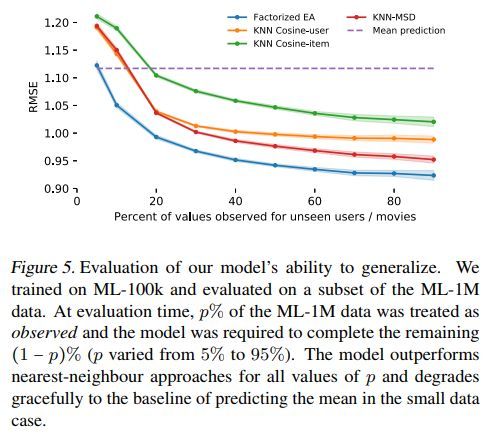
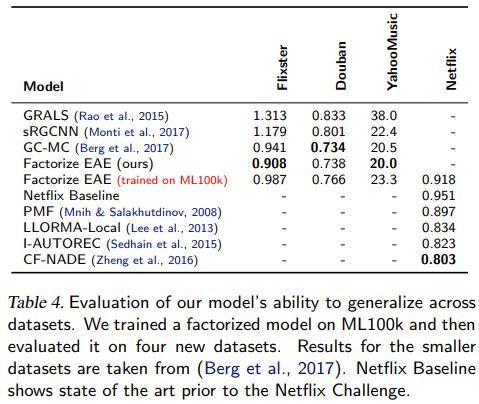
各方法的泛化能力对比如下
不同采样方法的影响如下
代码地址
Tensorflow: https://github.com/mravanba/deep_exchangeable_tensors. Pytorch: https: //github.com/jhartford/AutoEncSets
[3] ContextNet: Deep learning for Star Galaxy Classification
Noble Kennamer, David Kirkby, Alex Ihler, Javier Sanchez
University of California, Irvine
http://proceedings.mlr.press/v80/kennamer18a/kennamer18a.pdf
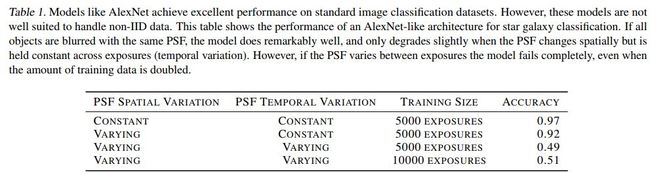
似AlexNet网络结果如下
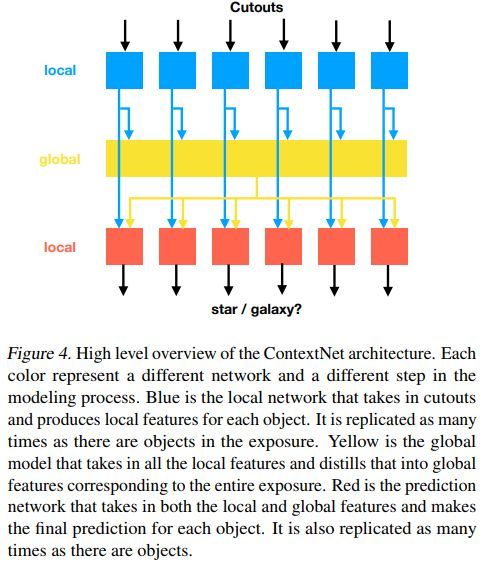
ContextNet网络概览如下
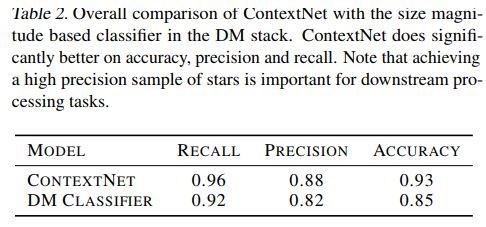
两种方法效果对比如下
代码地址
https://github.com/NobleKennamer/ContextNet
[4] First Order Generative Adversarial Networks
Calvin Seward, Thomas Unterthiner, Urs Bergmann, Nikolay Jetchev, Sepp Hochreiter
Zalando Research; LIT AI Lab & Institute of Bioinformatics, Johannes Kepler University Linz
http://proceedings.mlr.press/v80/seward18a/seward18a.pdf
定义一
对抗式分散度
定义二
临界对抗式散度
定义三
严格对抗散度
定义四
最佳临界对抗散度
两个假设
必要条件一
必要条件二
凸容许临界参数集
必要条件三
良义更新规则
必要条件四
低方差更新规则
定义五
个性化Wassertein 散度
定理一
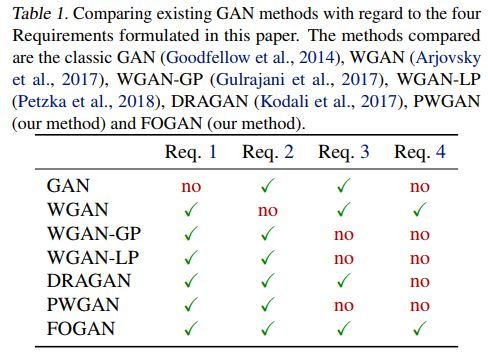
各种GAN的四个必要条件的对比如下
定义六
定理二
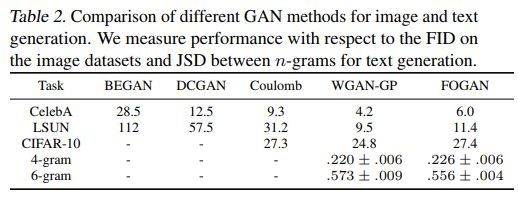
各方法效果对比如下
代码地址
https://github.com/zalandoresearch/first_order_gan
[5] Towards Binary-Valued Gates for Robust LSTM Training
Zhuohan Li, Di He, Fei Tian, Wei Chen, Tao Qin, Liwei Wang, Tie-Yan Liu
Peking University, Microsoft Research
http://proceedings.mlr.press/v80/li18c/li18c.pdf
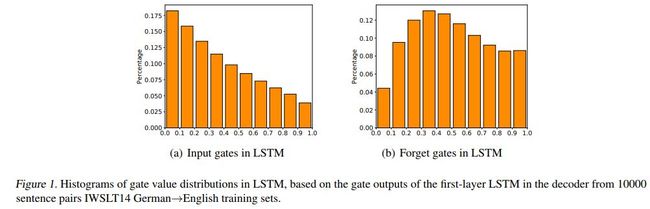
LSTM的输入门及遗忘门取值的直方图分布如下
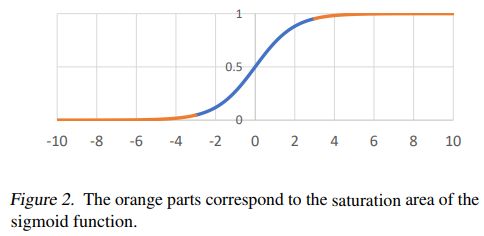
sigmoid函数的饱和区示例如下
命题一
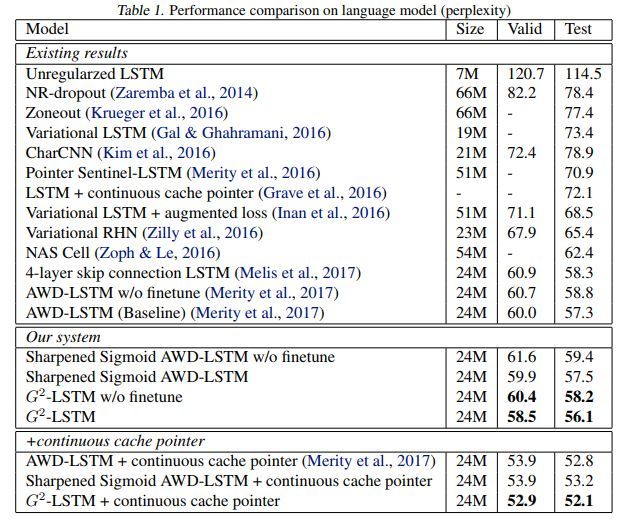
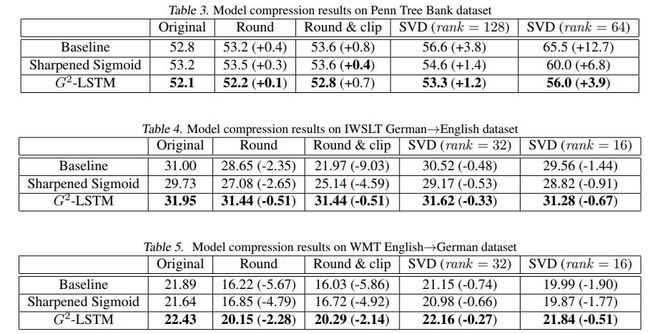
各方法在语言模型上的效果对比如下
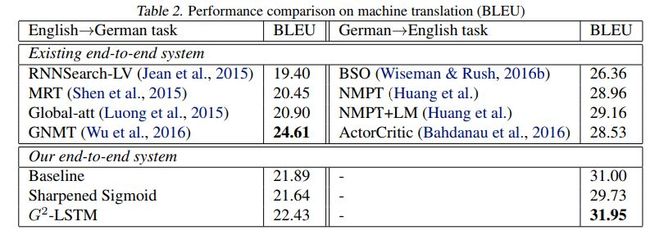
各方法在机器翻译任务中的对比如下
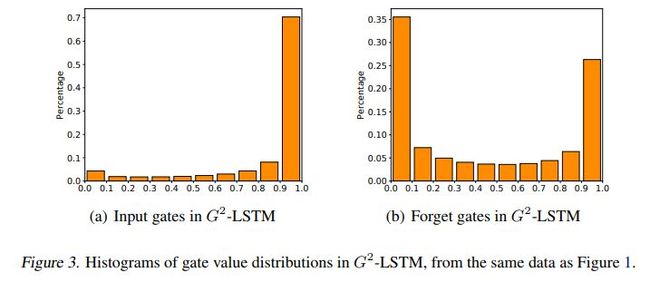
G2-LSTM的直方图如下
代码地址
https://github.com/zhuohan123/g2-lstm
您可能感兴趣